Comment appliquer le théorème central limite dans Excel

Le théorème central limite stipule que la distribution d’échantillonnage d’une moyenne d’échantillon est approximativement normale si la taille de l’échantillon est suffisamment grande, même si la distribution de la population n’est pas normale .

Le théorème central limite indique également que la distribution d’échantillonnage aura les propriétés suivantes :

1. La moyenne de la distribution d’échantillonnage sera égale à la moyenne de la distribution de la population :

x = µ

2. L’écart type de la distribution d’échantillonnage sera égal à l’écart type de la population divisé par la taille de l’échantillon :

s = σ / √n

Dans ce tutoriel, nous expliquons comment appliquer le théorème central limite dans Excel à une distribution donnée.

Application du théorème central limite dans Excel

Supposons que nous ayons une distribution avec une moyenne de 8 et un écart type de 4 . Nous pouvons utiliser les formules suivantes dans Excel pour trouver à la fois la moyenne et l’écart type de la distribution d’échantillonnage avec une taille d’échantillon de 15 :

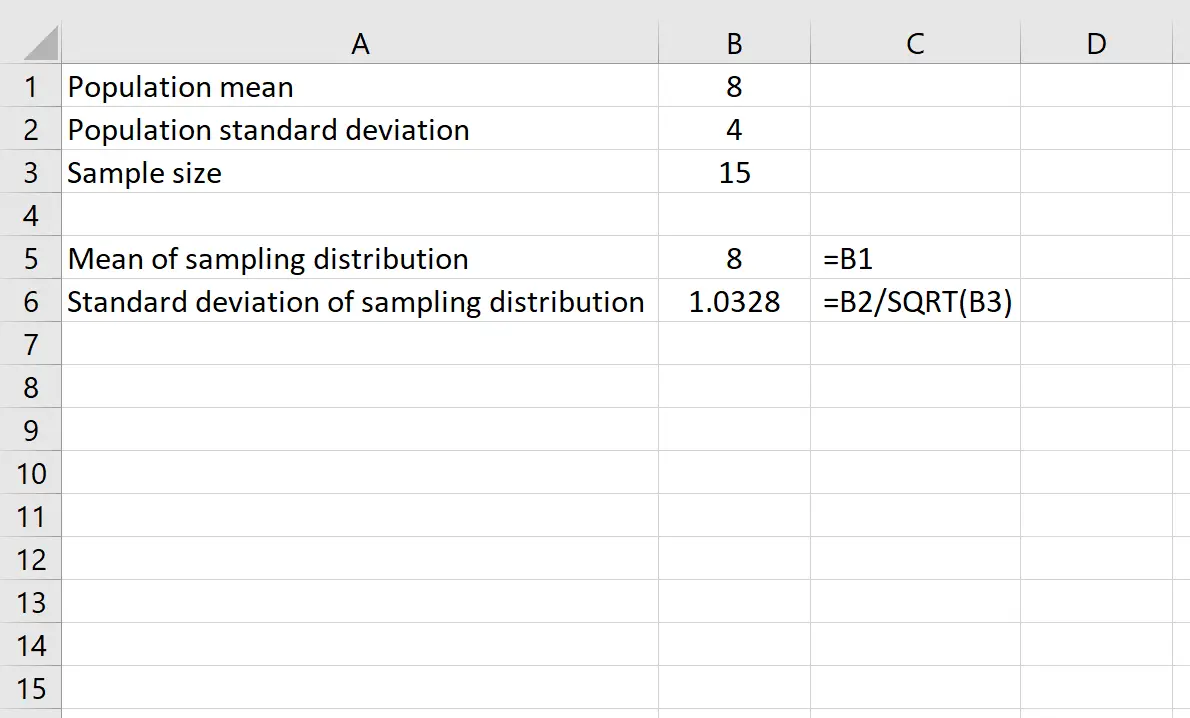
La moyenne de la distribution d’échantillonnage est simplement égale à la moyenne de la distribution de la population, qui est 8 .

L’écart type de la distribution d’échantillonnage est égal à l’écart type de la population divisé par la taille de l’échantillon, soit : 4 /√15 = 1,0328 .

Nous pouvons également utiliser le théorème central limite pour répondre à des questions sur les probabilités. Par exemple, si une population donnée a une moyenne de 8 et un écart type de 4 , quelle est la probabilité qu’un échantillon donné de taille 15   a une moyenne inférieure ou égale à 7 ?

Pour répondre à cette question, nous pouvons utiliser la fonction NORM.DIST() dans Excel, qui utilise la syntaxe suivante :

NORM.DIST(x, moyenne, standard_dev, cumulatif)

où:

• x : l’échantillon signifie que vous souhaitez tester
• moyenne : moyenne attendue de la distribution d’échantillonnage
• standard_dev : écart type attendu de la distribution d’échantillonnage
• cumulatif : TRUE renvoie la valeur du CDF normal ; FALSE renvoie la valeur du PDF normal. Dans notre cas, nous utiliserons toujours TRUE.

Cette fonction renverra la probabilité que la moyenne de l’échantillon soit inférieure ou égale à une certaine valeur.

Voici la formule que nous utiliserions dans cet exemple :

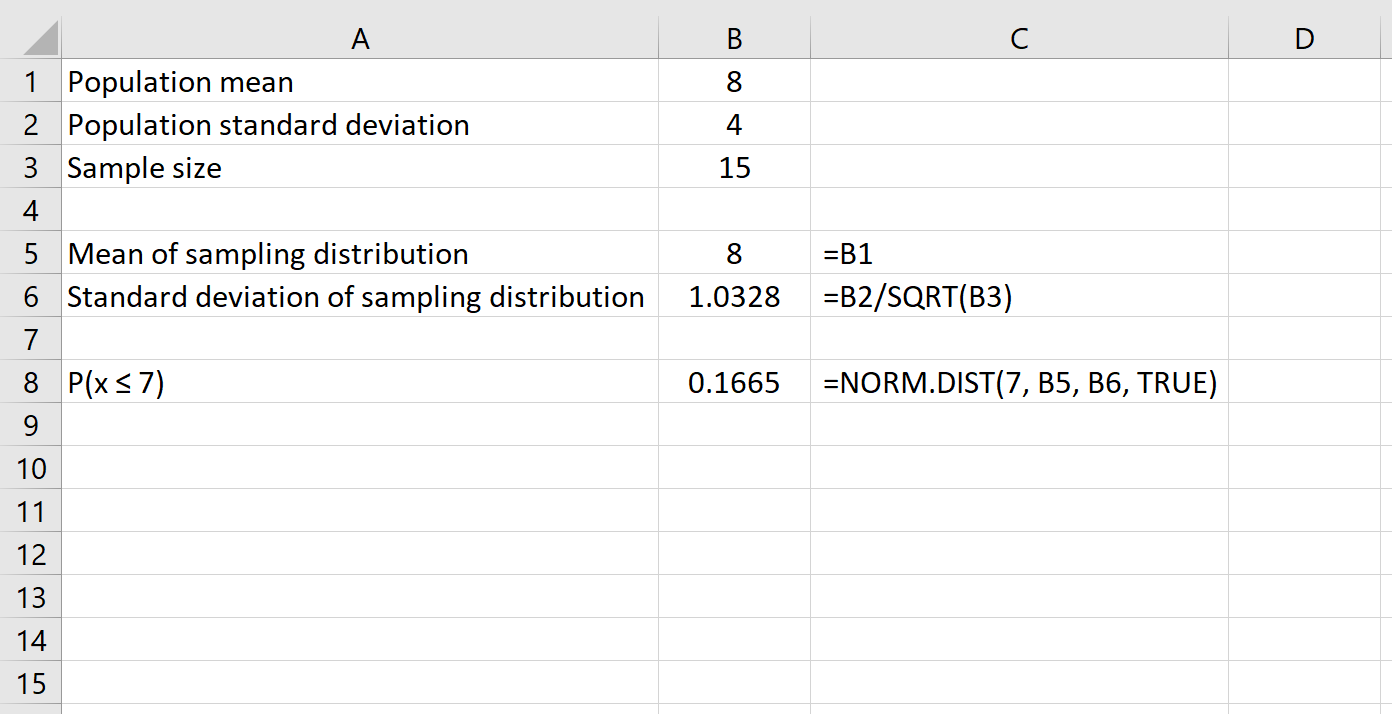
Cela nous indique que pour une population avec une moyenne de 8 et un écart type de 4 , la probabilité qu’un échantillon donné de taille 15   a une moyenne inférieure ou égale à 7 soit 0,1665 .

Nous pouvons également trouver la probabilité qu’une taille d’échantillon donnée ait une moyenne supérieure à un certain nombre en utilisant simplement la formule 1 – NORM.DIST() .

Par exemple, la formule suivante montre comment déterminer la probabilité qu’une taille d’échantillon donnée de 15 ait une moyenne supérieure à 7 :

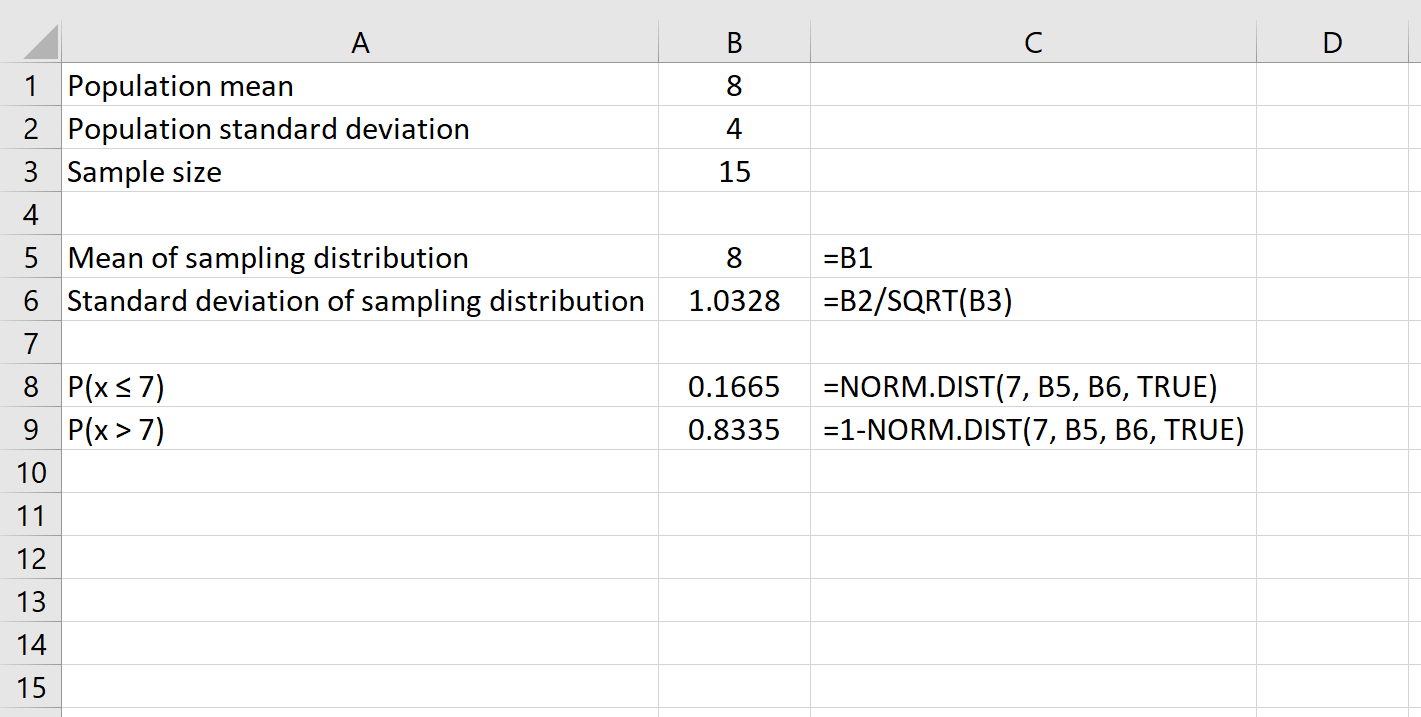
Enfin, nous pouvons trouver la probabilité qu’une taille d’échantillon donnée ait une moyenne entre deux nombres en utilisant la formule NORM.DIST(plus grand nombre) – NORM.DIST(plus petit nombre) .

Par exemple, la formule suivante montre comment trouver la probabilité qu’une taille d’échantillon donnée de 15 ait une moyenne comprise entre 7 et 9 :

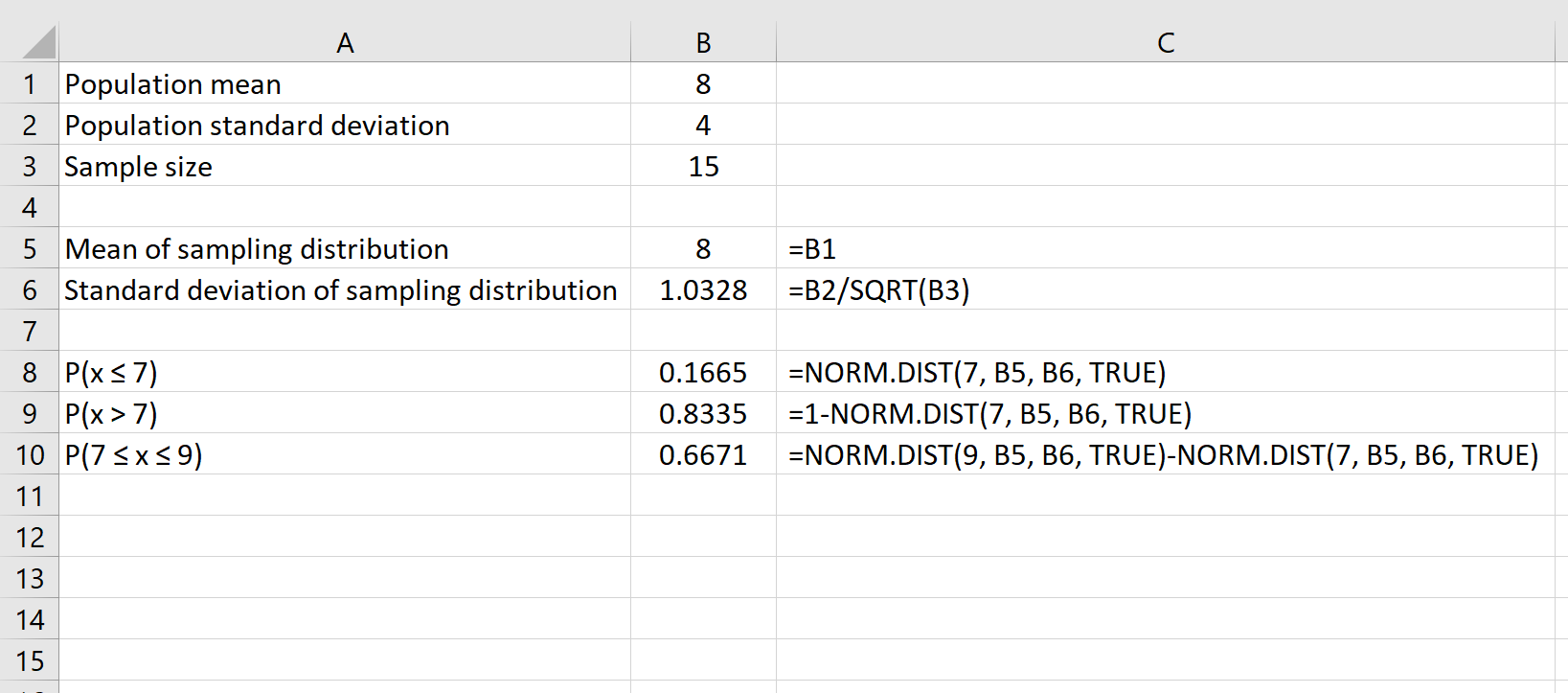
Ressources additionnelles

Calculateur du théorème central limite
Comment appliquer la règle empirique dans Excel
Comment créer une courbe en cloche dans Excel