Comment interpréter un tracé résiduel courbe (avec exemple)

Les tracés des résidus sont utilisés pour évaluer si les résidus d’un modèle de régression sont normalement distribués et s’ils présentent ou non une hétéroscédasticité .

Idéalement, vous souhaiteriez que les points d’un tracé résiduel soient dispersés de manière aléatoire autour d’une valeur de zéro, sans motif clair.

Si vous rencontrez un tracé résiduel dans lequel les points du tracé présentent un motif courbe, cela signifie probablement que le modèle de régression que vous avez spécifié pour les données n’est pas correct.

Dans la plupart des cas, cela signifie que vous avez tenté d’adapter un modèle de régression linéaire à un ensemble de données qui suit plutôt une tendance quadratique.

L’exemple suivant montre comment interpréter (et corriger) un tracé résiduel courbe dans la pratique.

Exemple : Interprétation d’un tracé résiduel courbe

Supposons que nous collections les données suivantes sur le nombre d’heures travaillées par semaine et le niveau de bonheur déclaré (sur une échelle de 0 à 100) pour 11 personnes différentes dans un bureau :

Si nous créons un simple nuage de points des heures travaillées par rapport au niveau de bonheur, voici à quoi cela ressemblerait :

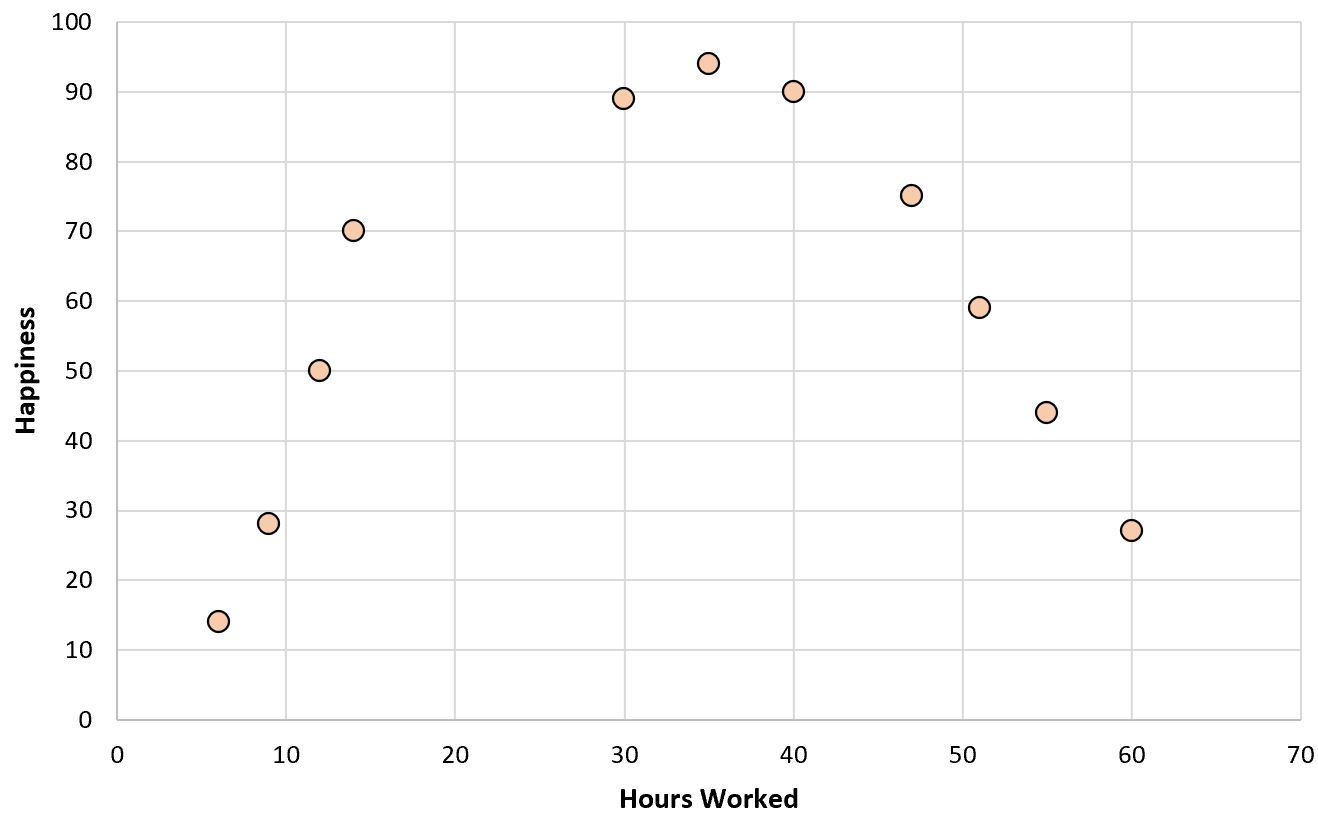
Supposons maintenant que nous souhaitions adapter un modèle de régression utilisant les heures travaillées pour prédire le niveau de bonheur.

Le code suivant montre comment adapter un modèle de régression linéaire simple à cet ensemble de données et produire un tracé résiduel dans R :

#create dataframe
df <- data.frame(hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                 happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#fit linear regression model
linear_model <- lm(happiness ~ hours, data=df)

#get list of residuals 
res <- resid(linear_model)

#produce residual vs. fitted plot
plot(fitted(linear_model), res, xlab='Fitted Values', ylab='Residuals')

#add a horizontal line at 0 
abline(0,0)

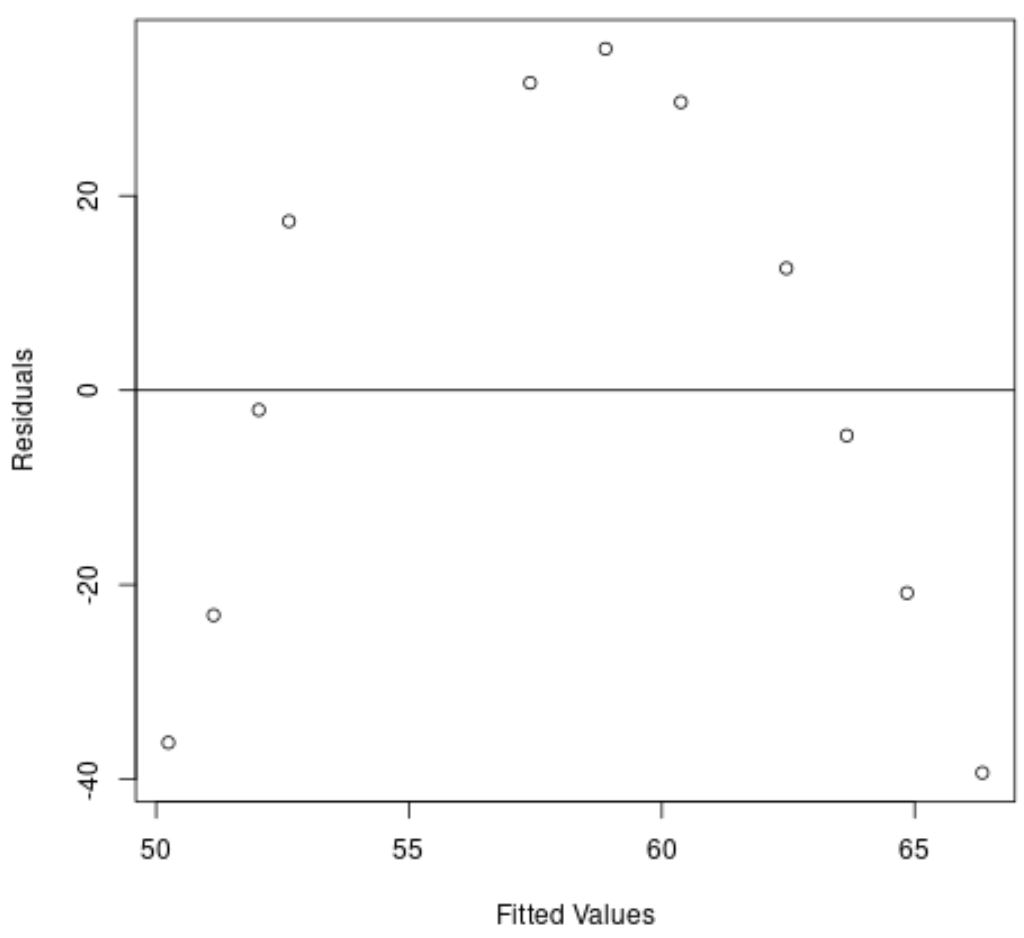
L’axe des x affiche les valeurs ajustées et l’axe des y affiche les résidus.

Sur le graphique, nous pouvons voir qu’il existe un motif courbe dans les résidus, ce qui indique qu’un modèle de régression linéaire ne fournit pas un ajustement approprié à cet ensemble de données.

Le code suivant montre comment adapter un modèle de régression quadratique à cet ensemble de données et produire un tracé résiduel dans R :

#create dataframe
df <- data.frame(hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                 happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#define quadratic term to use in model
df$hours2 <- df$hours^2

#fit quadratic regression model
quadratic_model <- lm(happiness ~ hours + hours2, data=df)

#get list of residuals 
res <- resid(quadratic_model)

#produce residual vs. fitted plot
plot(fitted(quadratic_model), res, xlab='Fitted Values', ylab='Residuals')

#add a horizontal line at 0 
abline(0,0)

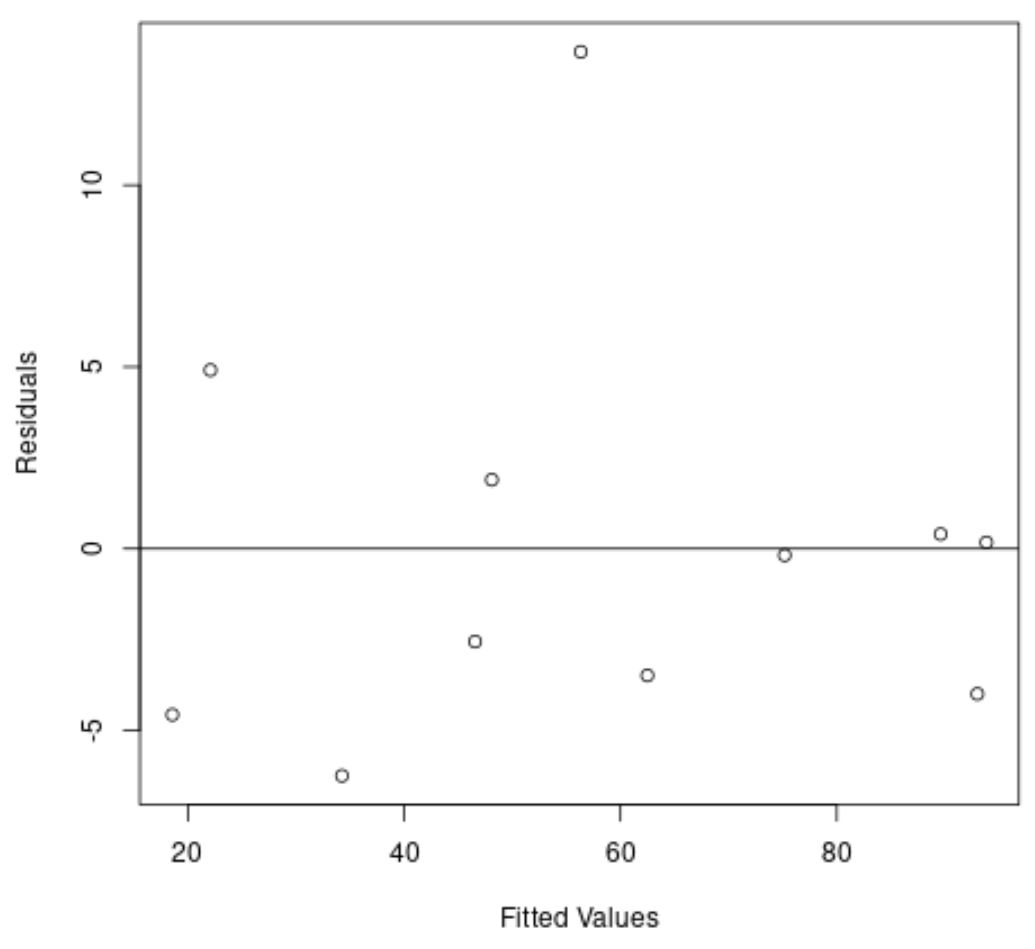
Une fois de plus, l’axe des x affiche les valeurs ajustées et l’axe des y affiche les résidus.

Sur le graphique, nous pouvons voir que les résidus sont dispersés de manière aléatoire autour de zéro et qu’il n’y a pas de tendance claire dans les résidus.

Cela nous indique qu’un modèle de régression quadratique réussit bien mieux à ajuster cet ensemble de données qu’un modèle de régression linéaire.

Cela devrait avoir du sens étant donné que nous avons vu que la véritable relation entre les heures travaillées et le niveau de bonheur semblait être quadratique plutôt que linéaire.

Ressources additionnelles

Les didacticiels suivants expliquent comment créer des tracés de résidus à l’aide de différents logiciels statistiques :

Comment créer un tracé résiduel à la main
Comment créer un tracé résiduel dans R
Comment créer un tracé résiduel dans Excel
Comment créer un tracé résiduel en Python