Comment tracer une distribution binomiale dans R

Pour tracer la fonction de masse de probabilité pour une distribution binomiale dans R, nous pouvons utiliser les fonctions suivantes :

• dbinom(x, size, prob) pour créer la fonction de masse de probabilité
• plot(x, y, type = ‘h’) pour tracer la fonction de masse de probabilité, en spécifiant que le tracé soit un histogramme (type=’h’)

Pour tracer la fonction de masse de probabilité, il suffit de spécifier la taille   (par exemple nombre d’essais) et prob (par exemple probabilité de succès sur un essai donné) dans la fonction dbinom() .

Par exemple, le code suivant illustre comment tracer une fonction de masse de probabilité pour une distribution binomiale avec taille = 20 et prob = 0,3 :

success <- 0:20

plot(success, dbinom(success, size=20, prob=.3),type='h')

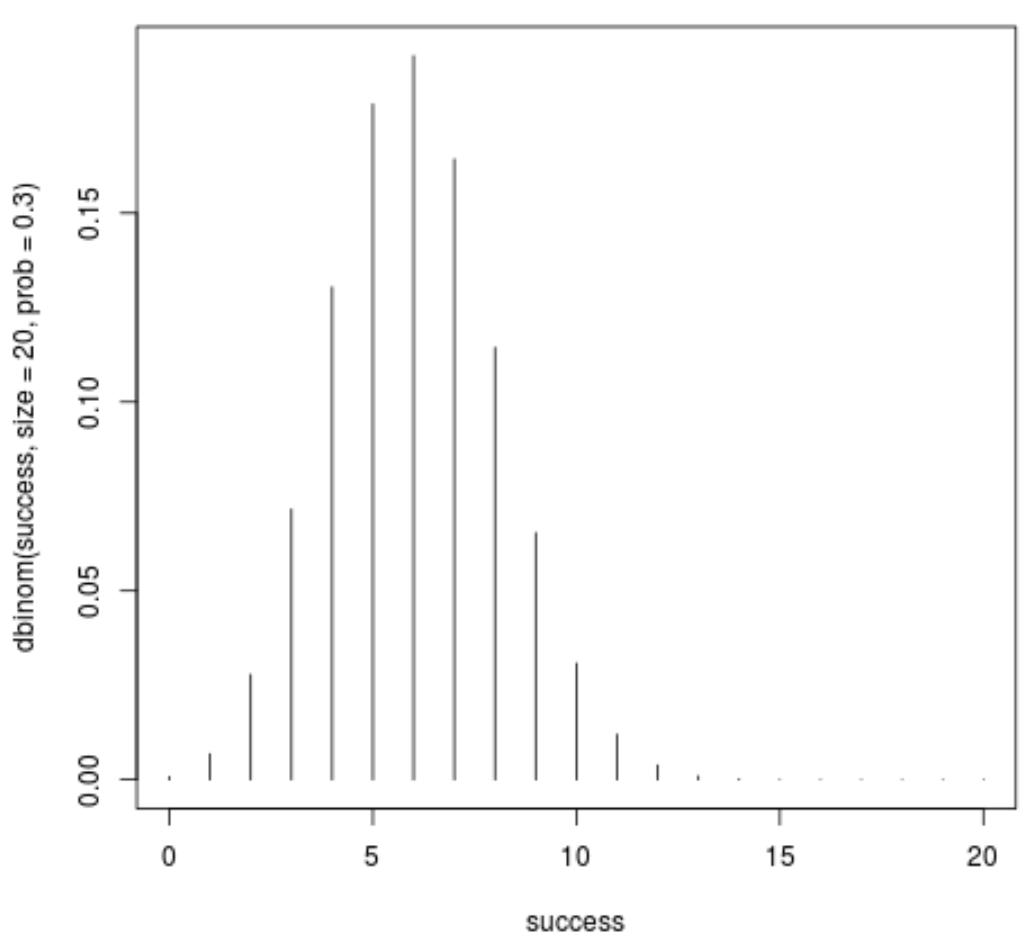
L’axe des x montre le nombre de réussites et l’axe des y montre la probabilité d’obtenir ce nombre de réussites en 20 essais.

Nous pouvons ajouter un titre, modifier les étiquettes des axes et augmenter la largeur des lignes pour rendre l’intrigue plus esthétique :

success <- 0:20

plot(success,dbinom(success,size=20,prob=.3),
     type='h',
     main='Binomial Distribution (n=20, p=0.3)',
     ylab='Probability',
     xlab ='# Successes',
     lwd=3)

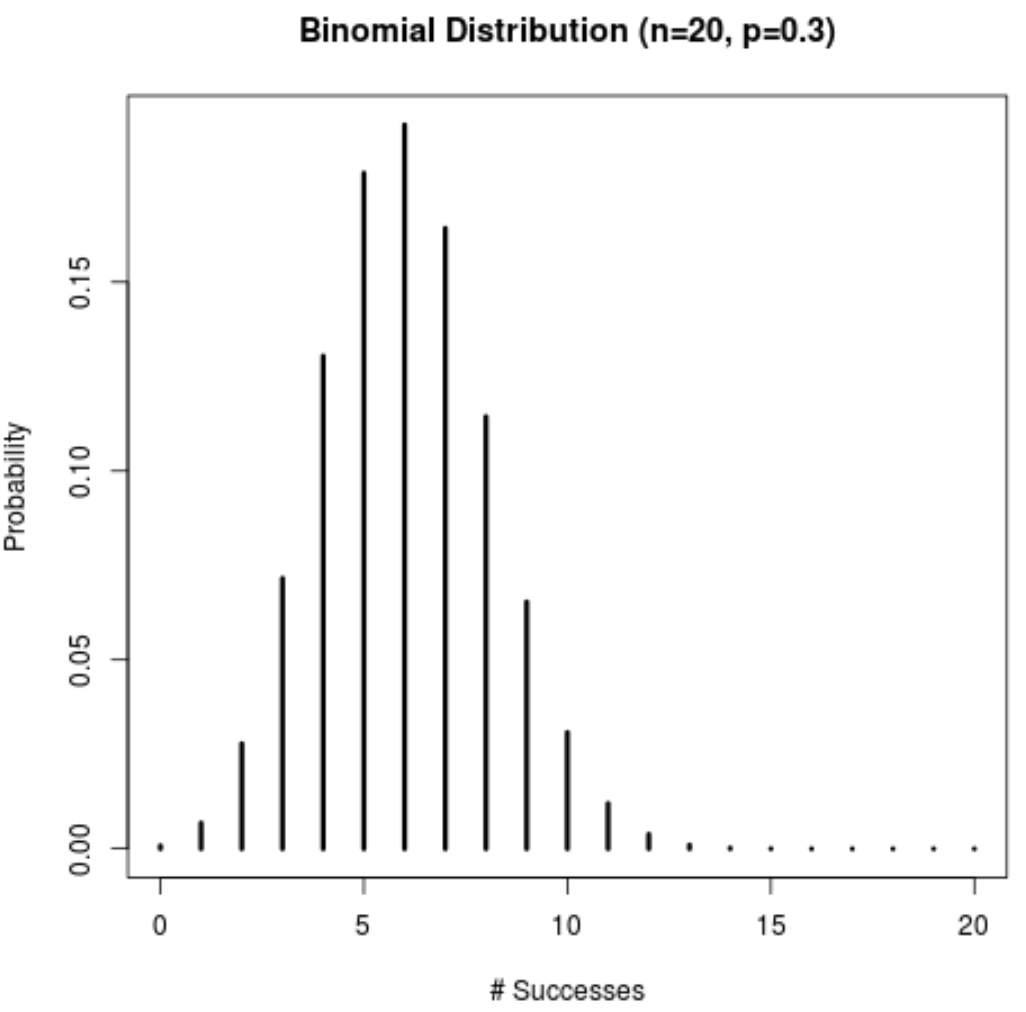
Vous pouvez utiliser le code suivant pour obtenir les probabilités réelles pour chaque nombre de réussites affiché dans le graphique :

#prevent R from displaying numbers in scientific notation 
options(scipen=999) 

#define range of successes
success <- 0:20

#display probability of success for each number of trials
dbinom(success, size=20, prob=.3)

[1] 0.00079792266297612 0.00683933711122388 0.02784587252426865
[4] 0.07160367220526231 0.13042097437387065 0.17886305056987975
[7] 0.19163898275344257 0.16426198521723651 0.11439673970486122
[10] 0.06536956554563482 0.03081708090008504 0.01200665489613703
[13] 0.00385928193090119 0.00101783259716075 0.00021810698510587
[16] 0.00003738976887529 0.00000500755833151 0.00000050496386536
[19] 0.00000003606884753 0.00000000162716605 0.00000000003486784

Ressources additionnelles

Une introduction à la distribution binomiale
Comprendre la forme d’une distribution binomiale