Comment tracer une courbe ROC en Python (étape par étape)

La régression logistique est une méthode statistique que nous utilisons pour ajuster un modèle de régression lorsque la variable de réponse est binaire. Pour évaluer dans quelle mesure un modèle de régression logistique s’adapte à un ensemble de données, nous pouvons examiner les deux métriques suivantes :

• Sensibilité : probabilité que le modèle prédise un résultat positif pour une observation alors que le résultat est effectivement positif. C’est ce qu’on appelle également le « taux de vrais positifs ».
• Spécificité : la probabilité que le modèle prédise un résultat négatif pour une observation alors que le résultat est effectivement négatif. C’est ce qu’on appelle également le « vrai taux négatif ».

Une façon de visualiser ces deux mesures consiste à créer une courbe ROC , qui signifie courbe « caractéristique de fonctionnement du récepteur ». Il s’agit d’un graphique qui affiche la sensibilité et la spécificité d’un modèle de régression logistique.

L’exemple étape par étape suivant montre comment créer et interpréter une courbe ROC en Python.

Étape 1 : Importer les packages nécessaires

Tout d’abord, nous allons importer les packages nécessaires pour effectuer une régression logistique en Python :

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
import matplotlib.pyplot as plt

Étape 2 : Ajuster le modèle de régression logistique

Ensuite, nous allons importer un ensemble de données et y adapter un modèle de régression logistique :

#import dataset from CSV file on Github
url = "https://raw.githubusercontent.com/Statology/Python-Guides/main/default.csv"
data = pd.read_csv(url)

#define the predictor variables and the response variable
X = data[['student', 'balance', 'income']]
y = data['default']

#split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=0) 

#instantiate the model
log_regression = LogisticRegression()

#fit the model using the training data
log_regression.fit(X_train,y_train)

Étape 3 : tracer la courbe ROC

Ensuite, nous calculerons le taux de vrais positifs et le taux de faux positifs et créerons une courbe ROC à l’aide du package de visualisation de données Matplotlib :

#define metrics
y_pred_proba = log_regression.predict_proba(X_test)[::,1]
fpr, tpr, _ = metrics.roc_curve(y_test,  y_pred_proba)

#create ROC curve
plt.plot(fpr,tpr)
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.show()

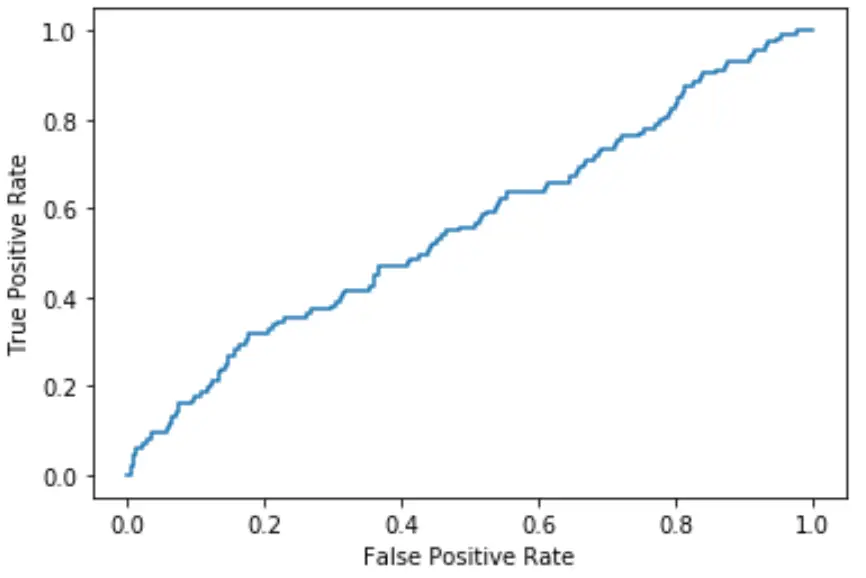
Plus la courbe épouse le coin supérieur gauche du tracé, plus le modèle parvient à classer les données en catégories.

Comme nous pouvons le voir sur le graphique ci-dessus, ce modèle de régression logistique réussit assez mal à classer les données en catégories.

Pour quantifier cela, nous pouvons calculer l’AUC – aire sous la courbe – qui nous indique quelle partie de la parcelle se trouve sous la courbe.

Plus l’AUC est proche de 1, meilleur est le modèle. Un modèle avec une AUC égale à 0,5 n’est pas meilleur qu’un modèle faisant des classifications aléatoires.

Étape 4 : Calculez l’ASC

Nous pouvons utiliser le code suivant pour calculer l’AUC du modèle et l’afficher dans le coin inférieur droit du tracé ROC :

#define metrics
y_pred_proba = log_regression.predict_proba(X_test)[::,1]
fpr, tpr, _ = metrics.roc_curve(y_test,  y_pred_proba)
auc = metrics.roc_auc_score(y_test, y_pred_proba)

#create ROC curve
plt.plot(fpr,tpr,label="AUC="+str(auc))
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.legend(loc=4)
plt.show()

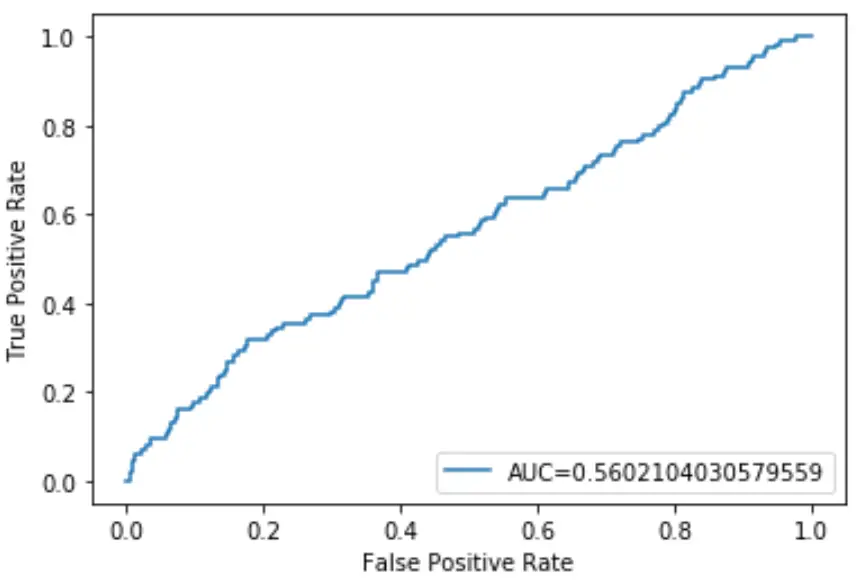
L’AUC de ce modèle de régression logistique s’avère être de 0,5602 . Comme ce chiffre est proche de 0,5, cela confirme que le modèle fait un mauvais travail de classification des données.

Connexe : Comment tracer plusieurs courbes ROC en Python