Comment transformer des données dans R (Log, racine carrée, racine cubique)

De nombreux tests statistiques supposent que les résidus d’une variable de réponse sont normalement distribués.

Cependant, les résidus ne sont souvent pas distribués normalement. Une façon de résoudre ce problème consiste à transformer la variable de réponse à l’aide de l’une des trois transformations suivantes :

1. Transformation du journal : transformez la variable de réponse de y en log(y) .

2. Transformation racine carrée : Transformez la variable de réponse de y en √ y .

3. Transformation de racine cubique : transformez la variable de réponse de y en y ^1/3 .

En effectuant ces transformations, la variable de réponse se rapproche généralement de la distribution normale. Les exemples suivants montrent comment effectuer ces transformations dans R.

Transformation du journal dans R

Le code suivant montre comment effectuer une transformation de journal sur une variable de réponse :

#create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform log transformation
log_y <- log10(df$y)

Le code suivant montre comment créer des histogrammes pour afficher la distribution de y avant et après avoir effectué une transformation de journal :

#create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for log-transformed distribution 
hist(log_y, col='coral2', main='Log Transformed')

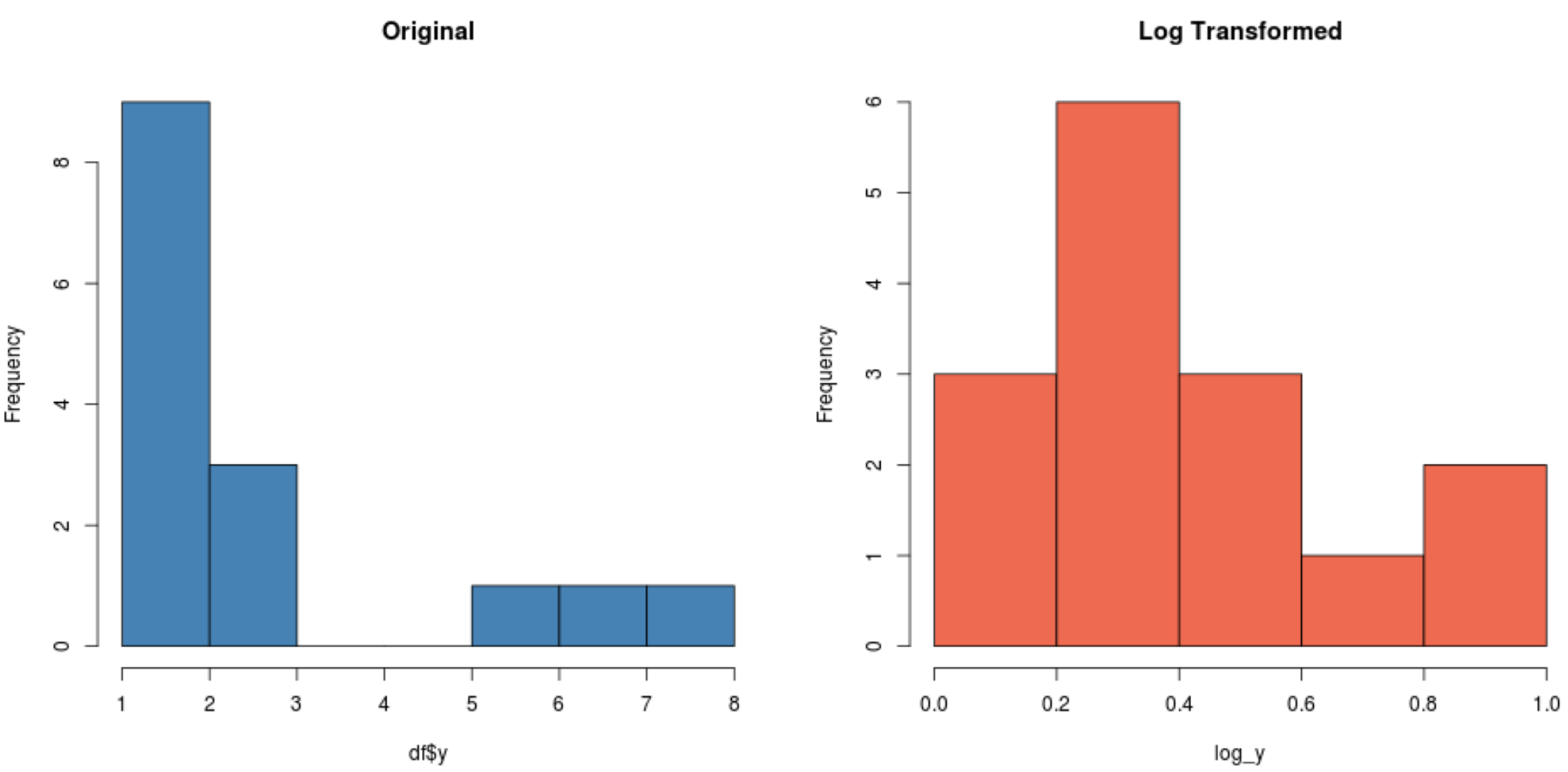
Remarquez à quel point la distribution transformée en log est beaucoup plus normale que la distribution d’origine. Ce n’est toujours pas une « forme de cloche » parfaite mais elle est plus proche d’une distribution normale que de la distribution originale.

En fait, si nous effectuons un test de Shapiro-Wilk sur chaque distribution, nous constaterons que la distribution d’origine échoue à l’hypothèse de normalité, contrairement à la distribution transformée en log (à α = 0,05) :

#perform Shapiro-Wilk Test on original data
shapiro.test(df$y)

	Shapiro-Wilk normality test

data:  df$y
W = 0.77225, p-value = 0.001655

#perform Shapiro-Wilk Test on log-transformed data 
shapiro.test(log_y)

	Shapiro-Wilk normality test

data:  log_y
W = 0.89089, p-value = 0.06917

Transformation racine carrée dans R

Le code suivant montre comment effectuer une transformation racine carrée sur une variable de réponse :

#create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform square root transformation
sqrt_y <- sqrt(df$y)

Le code suivant montre comment créer des histogrammes pour afficher la distribution de y avant et après avoir effectué une transformation racine carrée :

#create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for square root-transformed distribution 
hist(sqrt_y, col='coral2', main='Square Root Transformed')

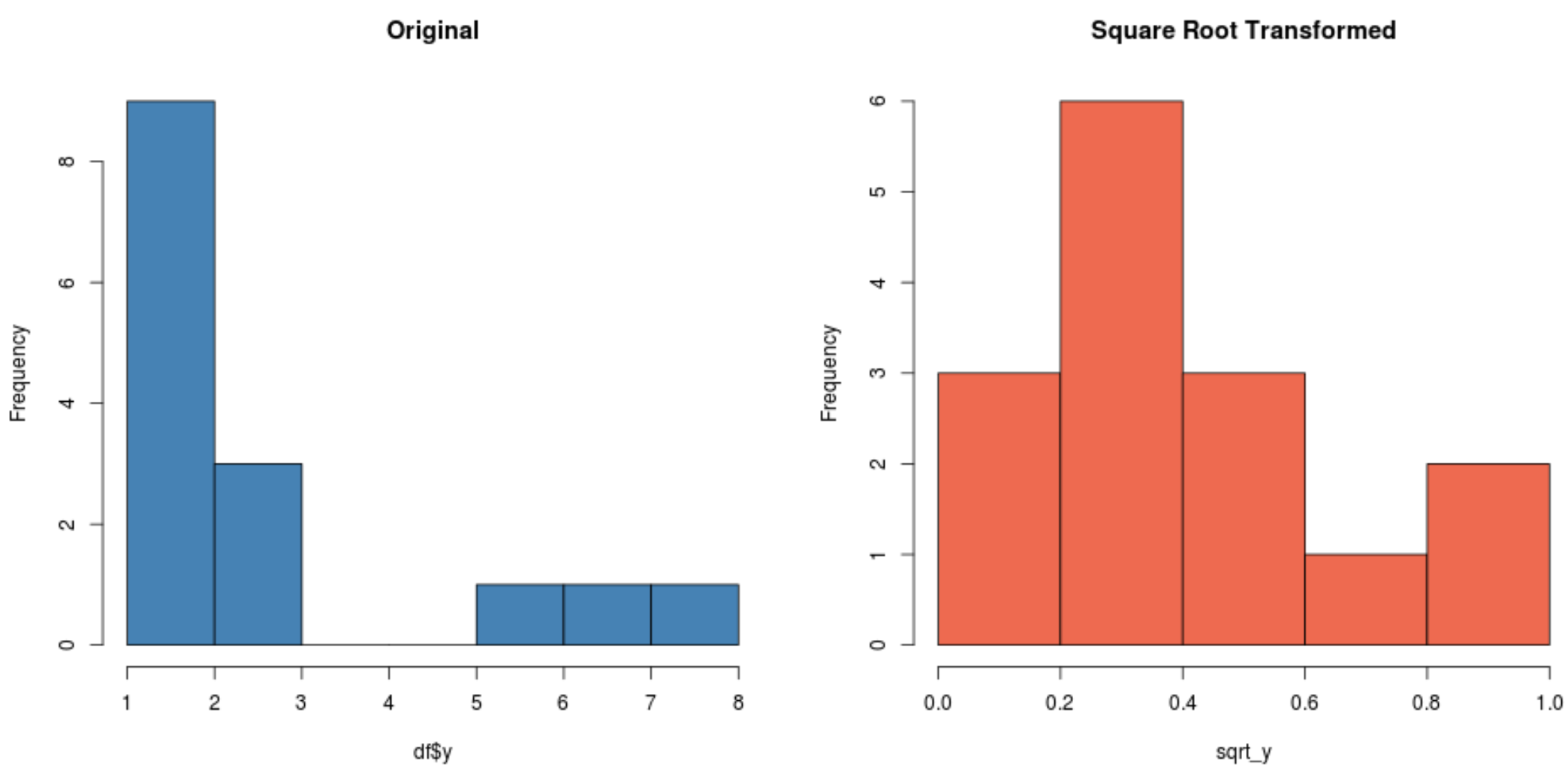
Remarquez comment la distribution transformée en racine carrée est beaucoup plus normalement distribuée que la distribution d’origine.

Transformation de racine cubique dans R

Le code suivant montre comment effectuer une transformation de racine cubique sur une variable de réponse :

#create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform square root transformation
cube_y <- df$y^(1/3)

Le code suivant montre comment créer des histogrammes pour afficher la distribution de y avant et après avoir effectué une transformation racine carrée :

#create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for square root-transformed distribution 
hist(cube_y, col='coral2', main='Cube Root Transformed')

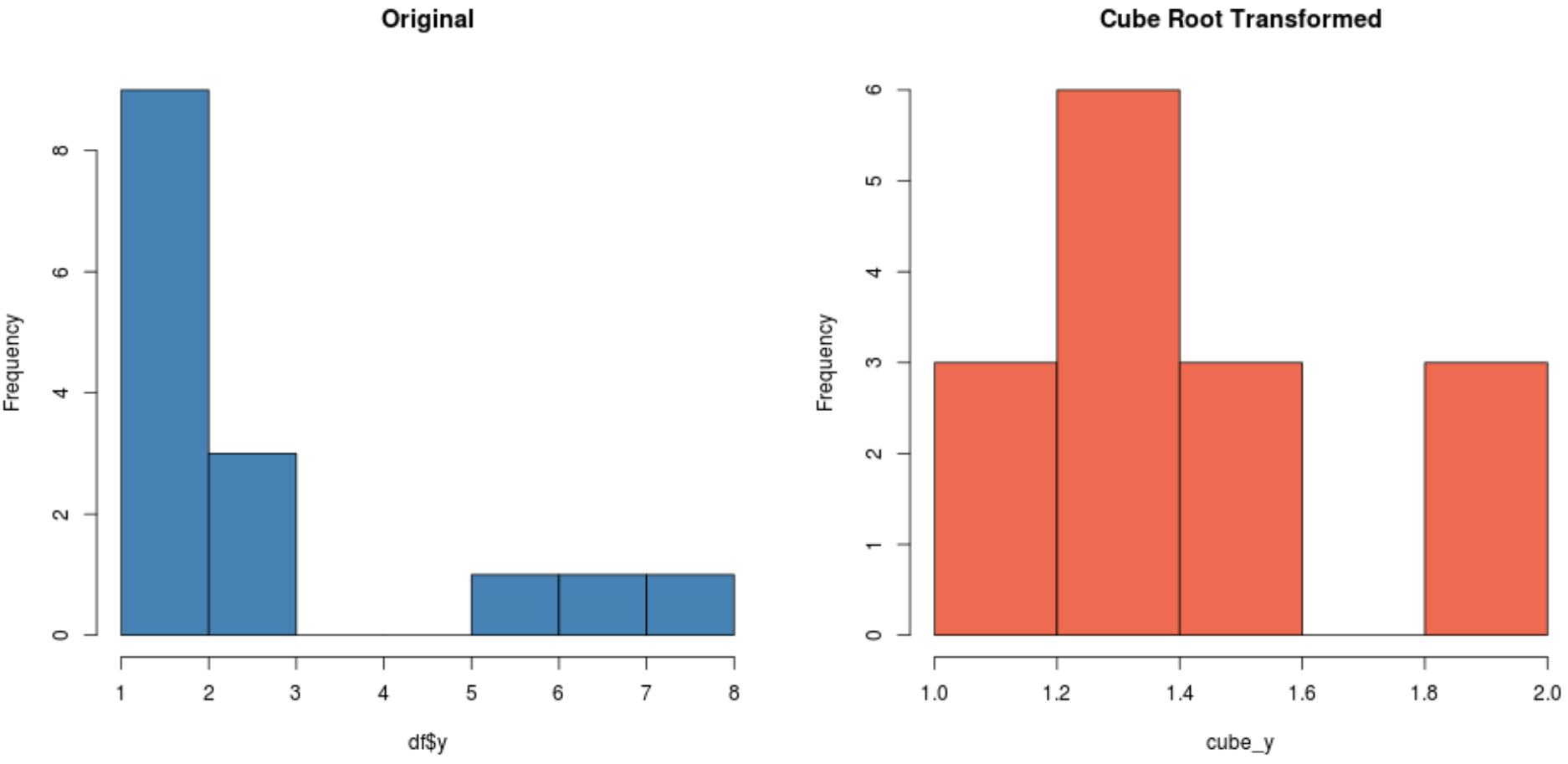
En fonction de votre ensemble de données, l’une de ces transformations peut produire un nouvel ensemble de données plus normalement distribué que les autres.