Comment trouver les scores Z dans une zone donnée (avec des exemples)

Il existe trois façons de trouver le score z qui correspond à une zone donnée sous une courbe de distribution normale

1. Utilisez la table z .

2. Utilisez le calculateur de centile du score Z.

3. Utilisez la fonction invNorm() sur une calculatrice TI-84 .

Les exemples suivants montrent comment utiliser chacune de ces méthodes pour trouver le score z qui correspond à une zone donnée sous une courbe de distribution normale.

Exemple 1 : Trouver la zone donnée du score Z à gauche

Trouvez le score z qui représente 15,62 % de l’aire de distribution à gauche.

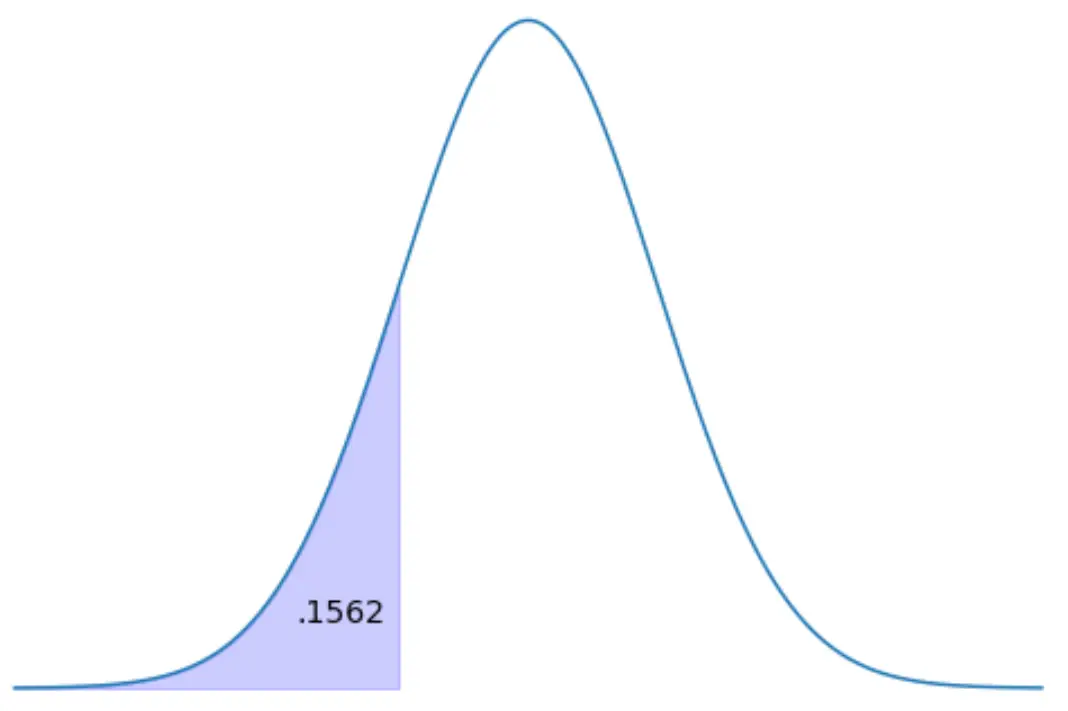
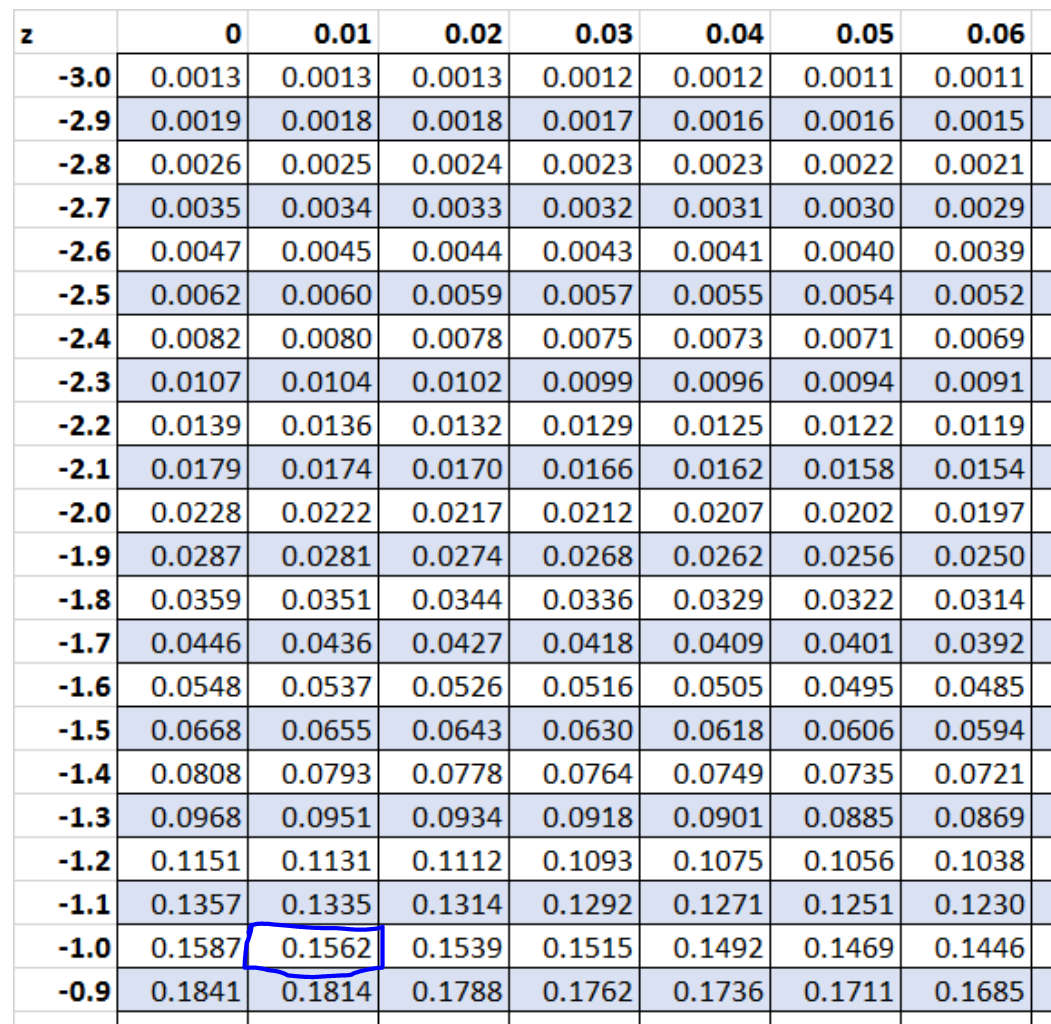
Méthode 1 : utilisez la table z.

Le score z qui correspond à une valeur de 0,1562 dans le tableau z est -1,01 .

2. Utilisez le calculateur de centile du score Z.

Selon le calculateur de centile au score Z , le score z qui correspond à un centile de 0,1562 est de -1,01 .

3. Utilisez la fonction invNorm() sur une calculatrice TI-84.

En utilisant la fonction invNorm() sur une calculatrice TI-84, le z-score qui correspond à une zone de 0,1562 à gauche est -1,01 .

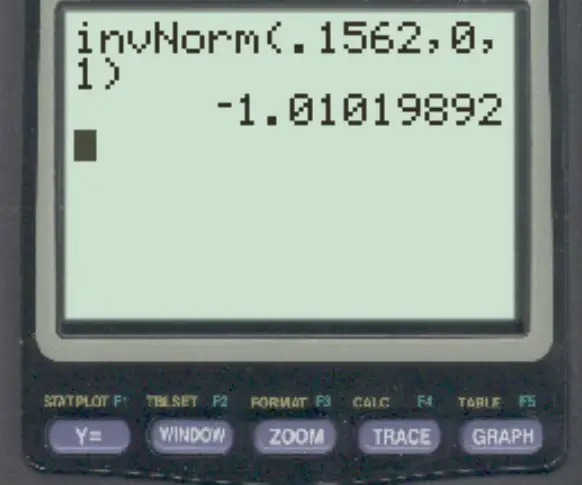
Notez que les trois méthodes conduisent au même résultat.

Exemple 2 : Trouver la zone donnée du score Z à droite

Trouvez le score z qui représente 37,83 % de l’aire de distribution à droite.

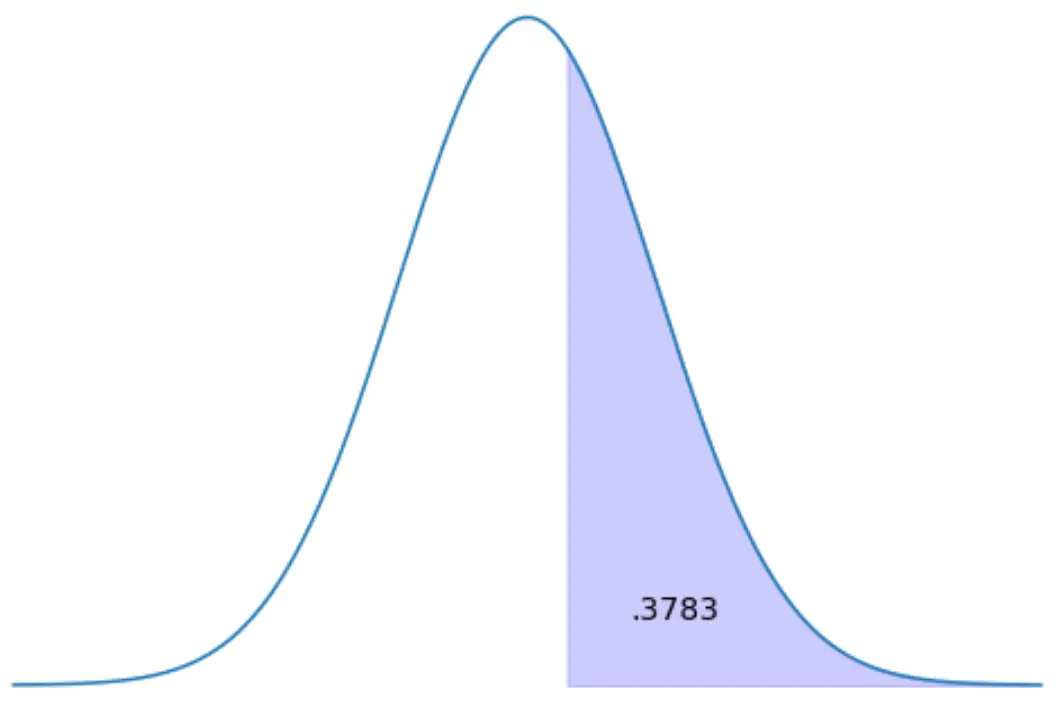
Méthode 1 : utilisez la table z.

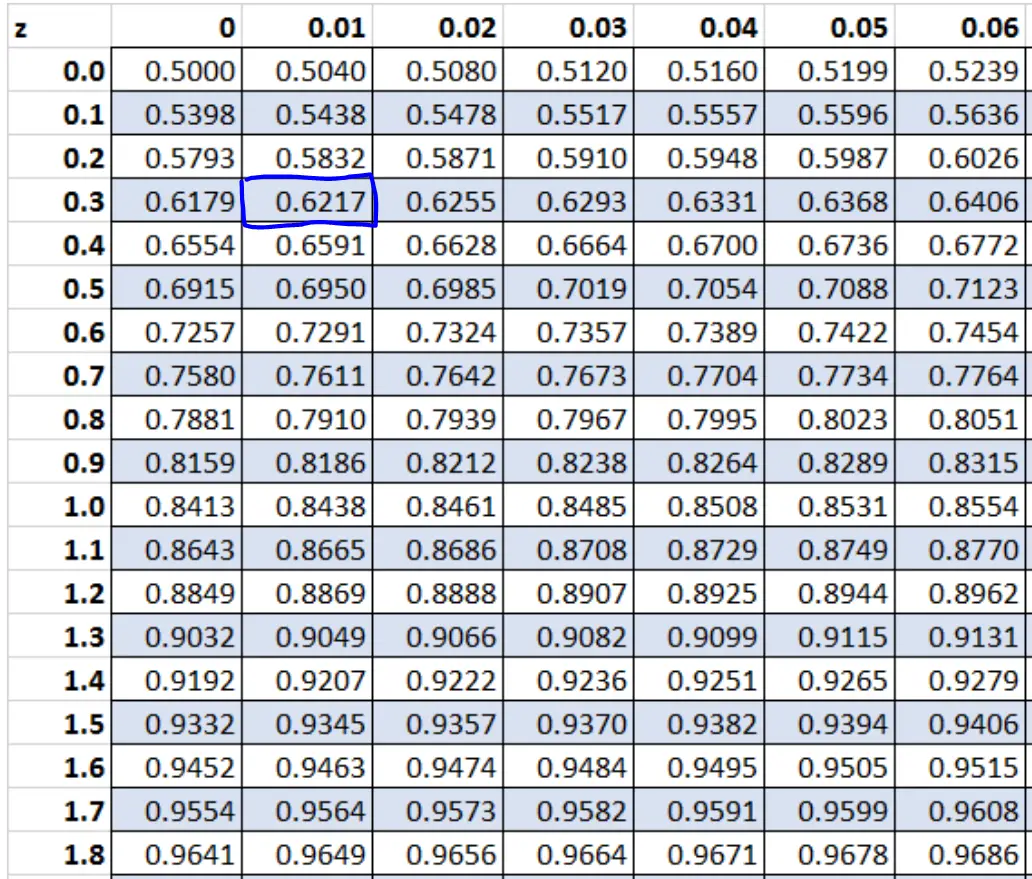
Le tableau z montre la zone à gauche des différents scores z. Ainsi, si nous savons que l’aire à droite est de 0,3783, alors l’aire à gauche est de 1 – 0,3783 = 0,6217.

Le score z qui correspond à une valeur de 0,6217 dans le tableau z est de 0,31.

2. Utilisez le calculateur de centile du score Z.

Selon le calculateur de centile au score Z , le score z qui correspond à un centile de 0,6217 est de . 3099 .

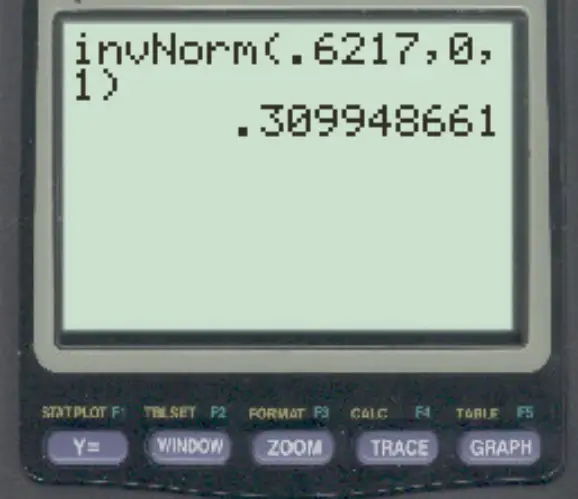
3. Utilisez la fonction invNorm() sur une calculatrice TI-84.

En utilisant la fonction invNorm() sur une calculatrice TI-84, le z-score qui correspond à une zone de .6217 à gauche est .3099 .

Exemple 3 : Trouver des scores Z dans la zone comprise entre deux valeurs

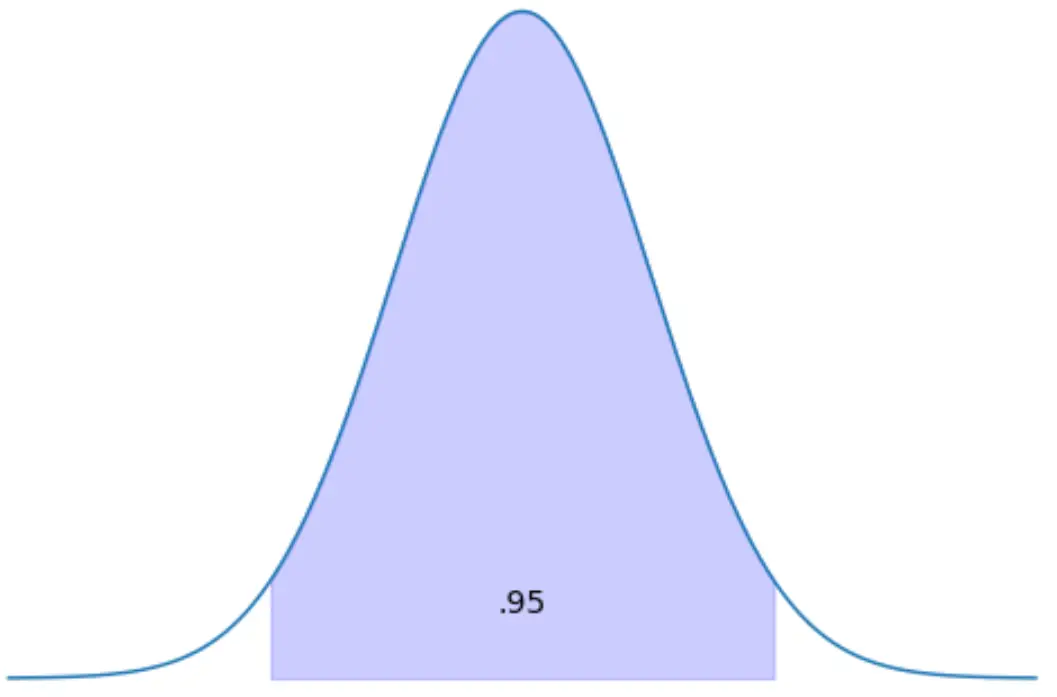
Trouvez les scores z qui ont entre eux 95 % de l’aire de distribution.

Méthode 1 : utilisez la table z.

Si 95 % de la distribution se situe entre deux scores z, cela signifie que 5 % de la distribution se situe en dehors des scores z.

Ainsi, 2,5 % de la distribution est inférieure à l’un des scores z et 2,5 % de la distribution est supérieure à l’autre score z.

Ainsi, nous pouvons rechercher 0,025 dans la table z. Le score z qui correspond à 0,025 dans le tableau z est -1,96 .

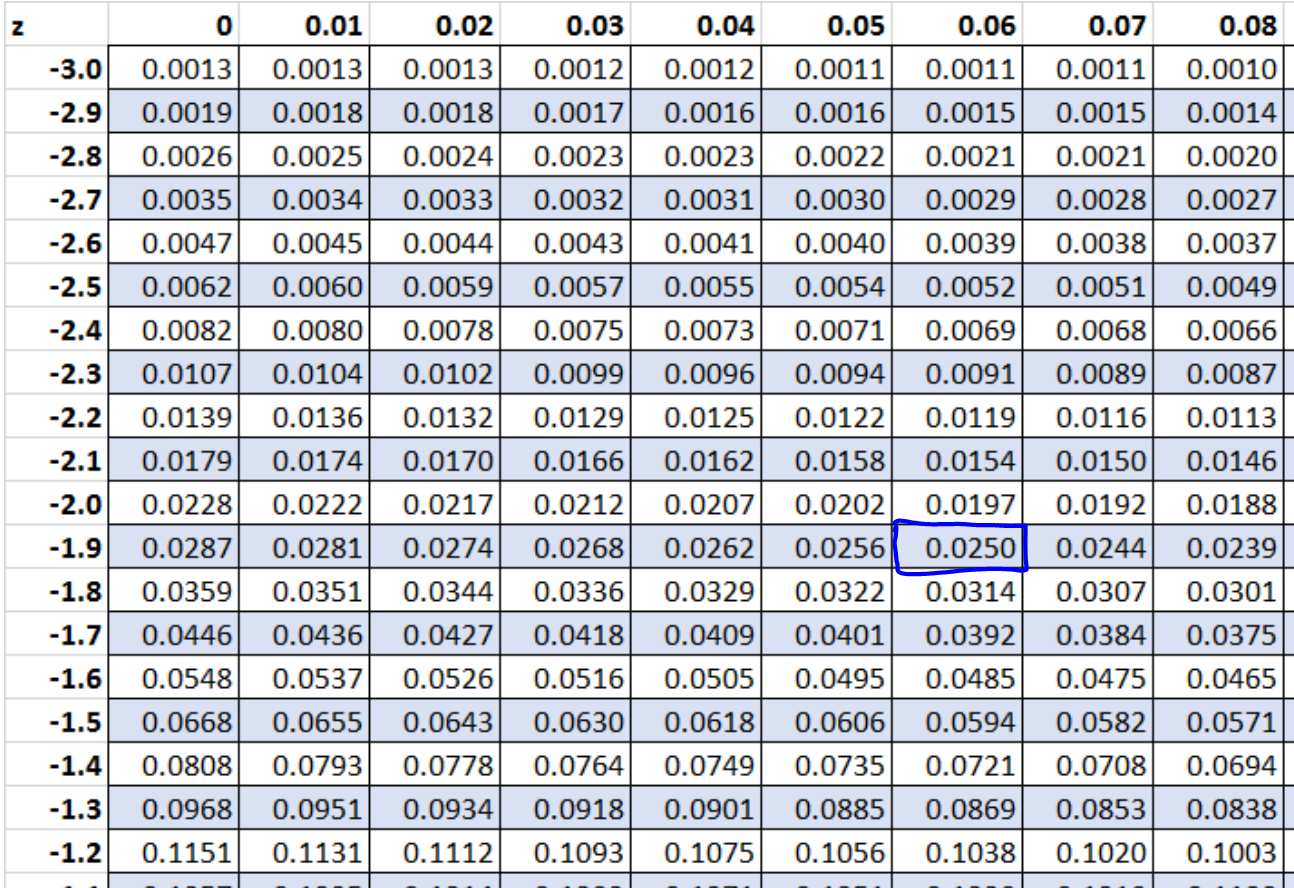
Ainsi, les scores z qui contiennent 95 % de la répartition entre eux sont -1,96 et 1,96 .

2. Utilisez le calculateur de centile du score Z.

Selon le calculateur de centile du score Z , le score z qui correspond à un centile de 0,025 est de -1,96 .

Ainsi, les scores z qui contiennent 95 % de la répartition entre eux sont -1,96 et 1,96 .

3. Utilisez la fonction invNorm() sur une calculatrice TI-84.

En utilisant la fonction invNorm() sur une calculatrice TI-84, le z-score qui correspond à une zone de 0,025 à gauche est -1,96 .

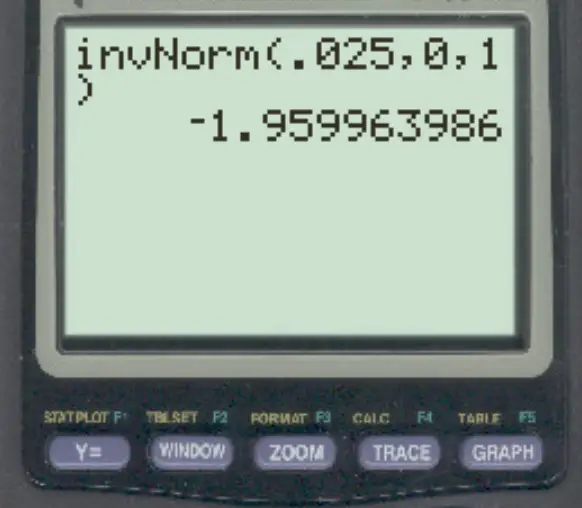
Ainsi, les scores z qui contiennent 95 % de la répartition entre eux sont -1,96 et 1,96 .