Comment trouver l’équation de régression linéaire à partir d’un tableau

Souvent, vous souhaiterez peut-être trouver une équation de régression linéaire à partir d’un tableau de données.

Par exemple, supposons que vous receviez le tableau de données suivant :

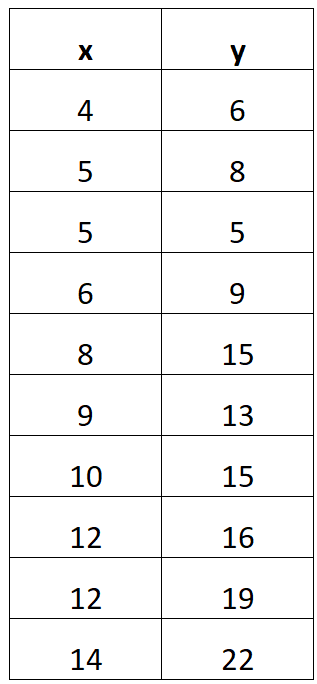
L’exemple suivant, étape par étape, explique comment trouver une équation de régression linéaire à partir de ce tableau de données.

Étape 1 : Calculer X*Y, X ² et Y ²

Tout d’abord, nous allons calculer les métriques suivantes pour chaque ligne :

• x*y
• ^x2
• et ²

La capture d’écran suivante montre comment procéder :

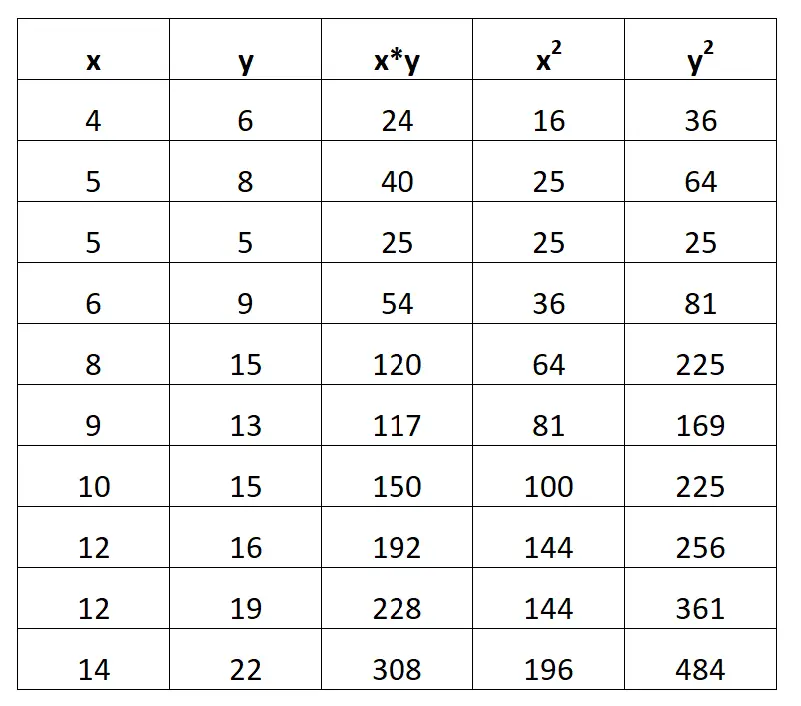
Étape 2 : Calculer ΣX, ΣY, ΣX*Y, ΣX ² et ΣY ²

Ensuite, nous calculerons la somme de chaque colonne :

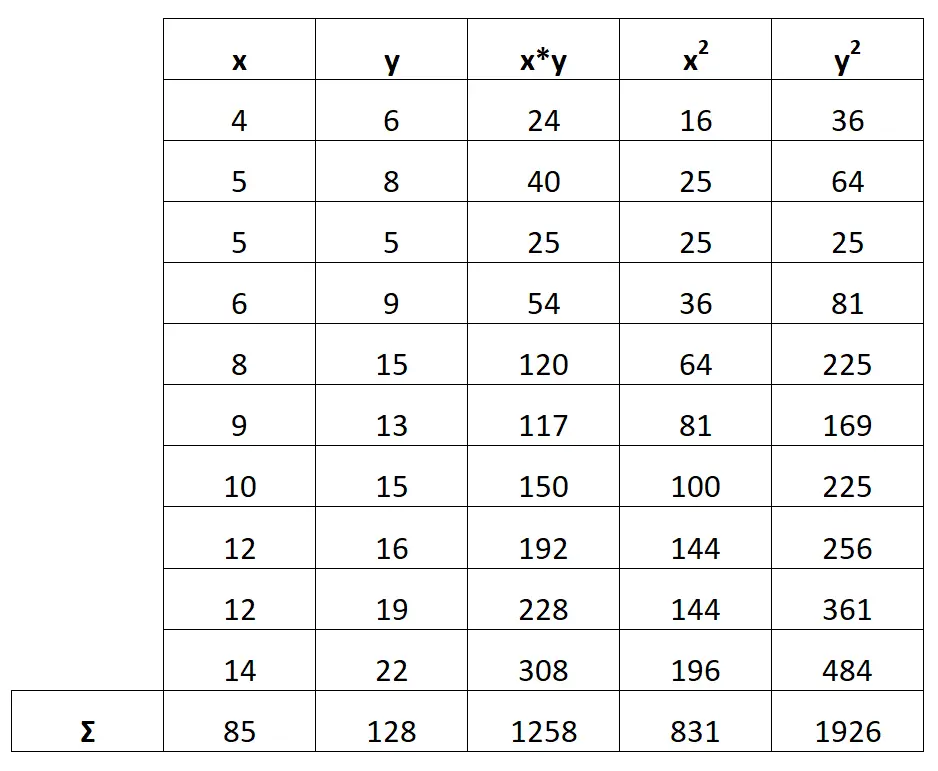
Étape 3 : Calculer b ₀

La formule pour calculer l’ordonnée à l’origine de l’équation de régression, b ₀ , est la suivante :

• b ₀ = ((Σy)(Σx ² ) – (Σx)(Σxy)) / (n(Σx ² ) – (Σx) ² )
• b ₀ = ((128)(831) – (85)(1258)) / (10(831) – (85) ² )
• b ₀ = -0,518

Remarque : Dans la formule, n représente le nombre total d’observations. Dans cet exemple, il y avait 10 observations au total.

Étape 4 : Calculer b ₁

La formule pour calculer la pente de l’équation de régression, b ₁ , est la suivante :

• b ₁ = (n(Σxy) – (Σx)(Σy)) / (n(Σx ² ) – (Σx) ² )
• b ₁ = (10(1258) – (85)(128)) / (10(831) – (85) ² )
• b ₁ = 1,5668

Étape 5 : Écrire l’équation de régression linéaire

L’équation de régression linéaire finale peut s’écrire :

• ŷ = b ₀ + b ₁ x

Ainsi, notre équation de régression linéaire s’écrirait comme suit :

• ŷ = -0,518 + 1,5668x

Nous pouvons vérifier que cette réponse est correcte en insérant les valeurs du tableau dans lecalculateur de régression linéaire simple :

Nous pouvons voir que l’équation de régression linéaire de la calculatrice correspond à celle que nous avons calculée manuellement.

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur la régression linéaire :

Introduction à la régression linéaire simple
Introduction à la régression linéaire multiple
Comment interpréter les coefficients de régression