Comment effectuer le test de Tukey dans R

Une ANOVA unidirectionnelle est utilisée pour déterminer s’il existe ou non une différence statistiquement significative entre les moyennes de trois groupes indépendants ou plus.

Si la valeur p globale du tableau ANOVA est inférieure à un certain niveau de signification, alors nous disposons de preuves suffisantes pour affirmer qu’au moins une des moyennes des groupes est différente des autres.

Cependant, cela ne nous dit pas quels groupes sont différents les uns des autres. Cela nous dit simplement que toutes les moyennes du groupe ne sont pas égales. Afin de savoir exactement quels groupes sont différents les uns des autres, nous devons effectuer un test post hoc .

L’un des tests post hoc les plus couramment utilisés est le test de Tukey , qui nous permet d’effectuer des comparaisons par paires entre les moyennes de chaque groupe tout en contrôlant le taux d’erreur par famille .

Ce tutoriel explique comment effectuer le test de Tukey dans R.

Remarque : Si l’un des groupes de votre étude est considéré comme un groupe témoin, vous devez plutôt utiliser le test de Dunnett comme test post-hoc.

Exemple : test de Tukey dans R

Étape 1 : Ajuster le modèle ANOVA.

Le code suivant montre comment créer un faux ensemble de données avec trois groupes (A, B et C) et ajuster un modèle ANOVA unidirectionnel aux données pour déterminer si les valeurs moyennes de chaque groupe sont égales :

#make this example reproducible
set.seed(0)

#create data
data <- data.frame(group = rep(c("A", "B", "C"), each = 30),
                   values = c(runif(30, 0, 3),
                                   runif(30, 0, 5),
                                   runif(30, 1, 7)))

#view first six rows of data
head(data)

  group     values
1     A  2.6900916
2     A  0.7965260
3     A  1.1163717
4     A  1.7185601
5     A  2.7246234
6     A  0.6050458

#fit one-way ANOVA model
model <- aov(values~group, data=data)

#view the model output
summary(model)

            Df Sum Sq Mean Sq F value   Pr(>F)    
group        2  98.93   49.46   30.83 7.55e-11 ***
Residuals   87 139.57    1.60                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Nous pouvons voir que la valeur p globale du tableau ANOVA est de 7,55e-11 . Puisque ce chiffre est inférieur à 0,05, nous disposons de suffisamment de preuves pour affirmer que les valeurs moyennes dans chaque groupe ne sont pas égales. Ainsi, nous pouvons procéder au test de Tukey pour déterminer exactement quelles moyennes de groupe sont différentes.

Étape 2 : Effectuez le test de Tukey.

Le code suivant montre comment utiliser la fonction TukeyHSD() pour effectuer le test de Tukey :

#perform Tukey's Test
TukeyHSD(model, conf.level=.95) 

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = values ~ group, data = data)

$group
         diff       lwr      upr     p adj
B-A 0.9777414 0.1979466 1.757536 0.0100545
C-A 2.5454024 1.7656076 3.325197 0.0000000
C-B 1.5676610 0.7878662 2.347456 0.0000199

La valeur p indique s’il existe ou non une différence statistiquement significative entre chaque programme. Les résultats montrent qu’il existe une différence statistiquement significative entre la perte de poids moyenne de chaque programme au niveau de signification de 0,05.

En particulier:

• Valeur P pour la différence de moyenne entre B et A : 0,0100545
• Valeur P pour la différence de moyenne entre C et A : 0,0000000
• Valeur P pour la différence de moyennes entre C et B : 0,0000199

Étape 3 : Visualisez les résultats.

Nous pouvons également utiliser la fonction plot(TukeyHSD()) pour visualiser les intervalles de confiance :

#plot confidence intervals
plot(TukeyHSD(model, conf.level=.95), las = 2)

Remarque : L’argument las spécifie que les étiquettes des graduations doivent être perpendiculaires (las=2) à l’axe.

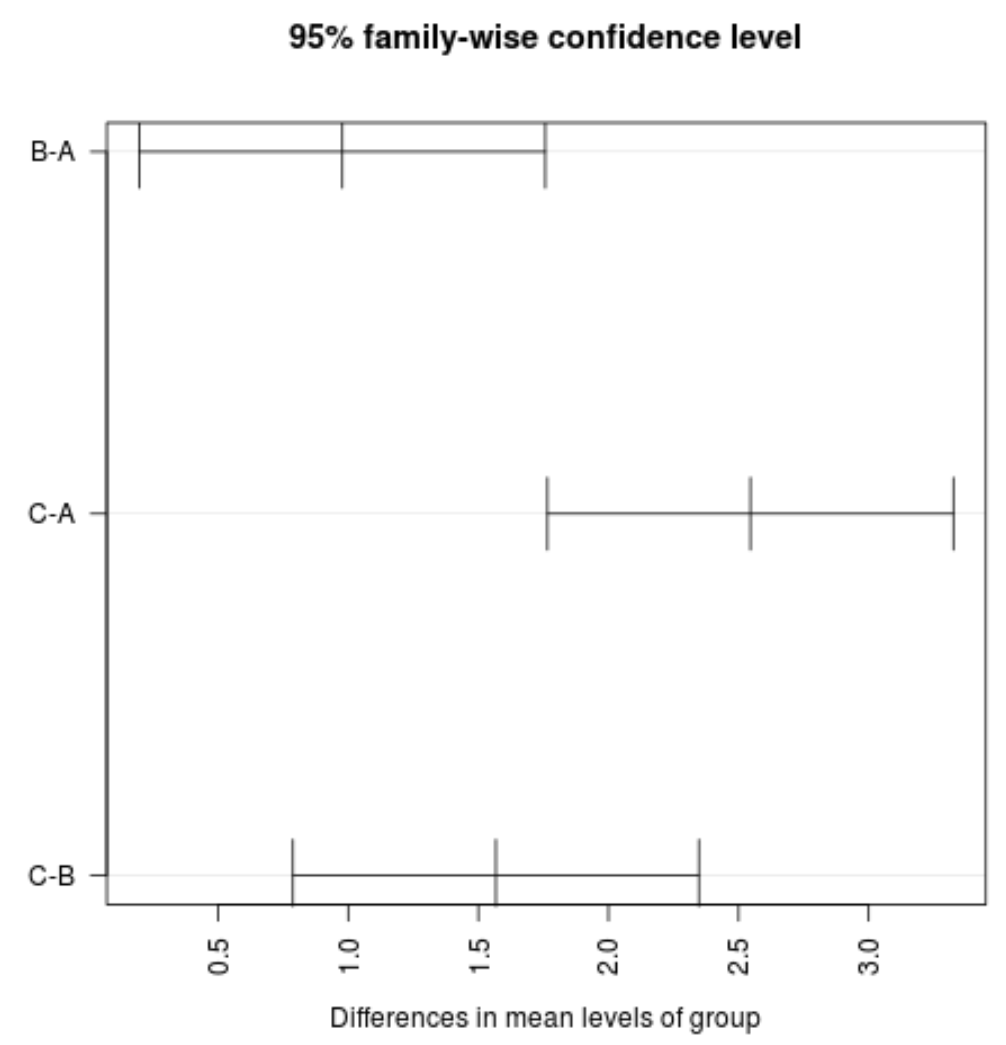
Nous pouvons voir qu’aucun des intervalles de confiance pour la valeur moyenne entre les groupes ne contient la valeur zéro, ce qui indique qu’il existe une différence statistiquement significative dans la perte moyenne entre les trois groupes. Cela concorde avec le fait que toutes les valeurs p de nos tests d’hypothèse sont inférieures à 0,05.

Pour cet exemple particulier, nous pouvons conclure ce qui suit :

• Les valeurs moyennes du groupe C sont nettement supérieures aux valeurs moyennes des groupes A et B.
• Les valeurs moyennes du groupe B sont nettement supérieures aux valeurs moyennes du groupe A.

Ressources additionnelles

Un guide d’utilisation des tests post-hoc avec ANOVA
Comment effectuer une ANOVA unidirectionnelle dans R
Comment effectuer une ANOVA bidirectionnelle dans R