Comment effectuer le test de Tukey dans SAS

Une ANOVA unidirectionnelle est utilisée pour déterminer s’il existe ou non une différence statistiquement significative entre les moyennes de trois groupes indépendants ou plus.

Si la valeur p globale du tableau ANOVA est inférieure à un certain niveau de signification, alors nous disposons de preuves suffisantes pour affirmer qu’au moins une des moyennes des groupes est différente des autres.

Cependant, cela ne nous dit pas quels groupes sont différents les uns des autres. Cela nous dit simplement que toutes les moyennes du groupe ne sont pas égales.

Afin de savoir exactement quels groupes sont différents les uns des autres, nous devons effectuer un test post hoc .

L’un des tests post hoc les plus couramment utilisés est le test de Tukey , qui nous permet d’effectuer des comparaisons par paires entre les moyennes de chaque groupe tout en contrôlant le taux d’erreur par famille .

L’exemple suivant montre comment effectuer le test de Tukey dans R.

Exemple : test de Tukey dans SAS

Supposons qu’un chercheur recrute 30 étudiants pour participer à une étude. Les étudiants sont assignés au hasard à utiliser l’une des trois méthodes d’étude pour se préparer à un examen.

Les résultats des examens pour chaque étudiant sont présentés ci-dessous :

Nous pouvons utiliser le code suivant pour créer cet ensemble de données dans SAS :

/*create dataset*/
data my_data;
    input Method $ Score;
    datalines;
A 78
A 81
A 82
A 82
A 85
A 88
A 88
A 90
B 81
B 83
B 83
B 85
B 86
B 88
B 90
B 91
C 84
C 88
C 88
C 89
C 90
C 93
C 95
C 98
;
run;

Ensuite, nous utiliserons proc ANOVA pour effectuer l’ANOVA unidirectionnelle :

/*perform one-way ANOVA*/
proc ANOVA data=my_data;
class Method;
model Score = Method;
means Method / tukey cldiff;
run;

Remarque : Nous avons utilisé l’énoncé des moyennes ainsi que les options tukey et cldiff pour spécifier qu’un test post-hoc de Tukey doit être effectué (avec des intervalles de confiance) si la valeur p globale de l’ANOVA unidirectionnelle est statistiquement significative.

Tout d’abord, nous analyserons le tableau ANOVA dans le résultat :

De ce tableau nous pouvons voir :

• La valeur F globale : 5,26
• La valeur p correspondante : 0,0140

Rappelons qu’une ANOVA unidirectionnelle utilise les hypothèses nulles et alternatives suivantes :

• H ₀ : Toutes les moyennes de groupe sont égales.
• H _A : Au moins une moyenne de groupe est différente   du reste.

Puisque la valeur p du tableau ANOVA (0,0140) est inférieure à α = 0,05, nous rejetons l’hypothèse nulle.

Cela nous indique que la note moyenne à l’examen n’est pas égale entre les trois méthodes d’étude.

Connexes : Comment interpréter la valeur F et la valeur P dans l’ANOVA

Pour déterminer exactement quelles moyennes de groupe sont différentes, nous devons nous référer au tableau final du résultat qui montre les résultats des tests post-hoc de Tukey :

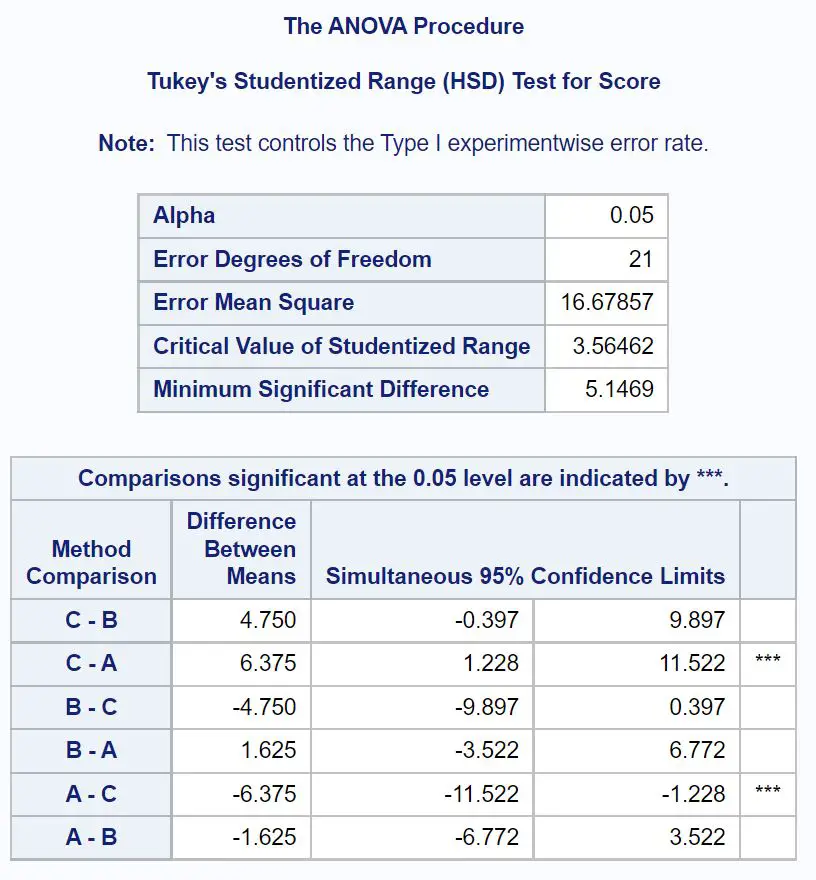
Pour savoir quelles moyennes de groupe sont différentes, nous devons examiner quelles comparaisons par paires ont des étoiles ( *** ) à côté d’elles.

D’après le tableau, nous pouvons voir qu’il existe une différence statistiquement significative dans les résultats moyens aux examens entre le groupe A et le groupe C.

Il n’y a pas de différences statistiquement significatives entre les moyennes des autres groupes.

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur les modèles ANOVA :

Un guide d’utilisation des tests post-hoc avec ANOVA
Comment effectuer une ANOVA unidirectionnelle dans SAS
Comment effectuer une ANOVA bidirectionnelle dans SAS