Tukey contre Bonferroni contre Scheffe : quel test devriez-vous utiliser ?

Une ANOVA unidirectionnelle est utilisée pour déterminer s’il existe ou non une différence statistiquement significative entre les moyennes de trois groupes indépendants ou plus.

Si la valeur p globale du tableau ANOVA est inférieure à un certain niveau de signification, alors nous disposons de preuves suffisantes pour affirmer qu’au moins une des moyennes des groupes est différente des autres.

Cependant, cela ne nous dit pas quels groupes sont différents les uns des autres. Cela nous dit simplement que toutes les moyennes du groupe ne sont pas égales.

Afin de savoir exactement quels groupes sont différents les uns des autres, nous devons effectuer un test post-hoc capable de contrôler le taux d’erreur par famille .

Trois des tests post-hoc les plus couramment utilisés comprennent :

• La méthode Tukey
• La méthode Scheffe
• La méthode Bonferroni

Ce didacticiel fournit un aperçu de chaque méthode ainsi que des instructions sur le test post-hoc à utiliser en fonction de la situation.

La méthode Tukey

Le test post-hoc de Tukey doit être utilisé lorsque vous souhaitez effectuer des comparaisons par paires entre les moyennes des groupes lorsque les tailles d’échantillon de chaque groupe sont égales.

Si les tailles d’échantillon ne sont pas égales, vous pouvez utiliser une version modifiée du test connue sous le nom de test de Tukey-Kramer.

Le terme « par paire » signifie que nous souhaitons comparer uniquement les moyennes de deux groupes à la fois.

Par exemple, supposons que nous ayons trois groupes : A, B, C.

Le test post-hoc de Tukey nous permettrait de faire les comparaisons par paires suivantes :

• _µA = _µB
• _µA = _µC
• _μB = _μC

Notez que pour k groupes, il existe un total de k ( k -1)/2 comparaisons par paires possibles.

La méthode Scheffe

Le test post-hoc de Scheffe est à utiliser lorsque l’on souhaite faire tous les contrastes possibles entre les moyennes des groupes. Ce test permet de comparer plus de deux moyennes à la fois, contrairement au test post-hoc de Tukey.

Par exemple, supposons que nous ayons quatre groupes : A, B, C, D.

Le test post-hoc de Scheffe permettrait de faire des comparaisons complexes telles que :

• _μA – _μB = _μC – _μD
• _μA + _μD = _μB + _μC

Bien que le test post-hoc de Scheffe soit le plus flexible, il est également le plus conservateur et produit les intervalles de confiance les plus larges. Cela signifie qu’il a la puissance statistique la plus faible et la capacité la plus faible à détecter de véritables différences entre les groupes.

Notez que le test post-hoc de Scheffe peut être utilisé que les tailles d’échantillon de groupe soient égales ou non.

La méthode Bonferroni

Le test post-hoc de Bonferroni doit être utilisé lorsque vous souhaitez effectuer au préalable un ensemble de comparaisons planifiées .

Par exemple, supposons que nous ayons trois groupes – A, B, C – et que nous sachions à l’avance que seules les comparaisons suivantes nous intéressent :

• _µA = _µB
• _μB = _μC

Lorsque nous avons un ensemble spécifique de comparaisons planifiées que nous aimerions effectuer à l’avance comme celui-ci, le test post-hoc de Bonferroni produit les intervalles de confiance les plus étroits, ce qui signifie qu’il a la plus grande capacité à détecter la véritable différence entre les groupes d’intérêt. .

Notez que le test post-hoc de Bonferroni peut également être utilisé que les tailles d’échantillon de groupe soient égales ou non.

Quelle méthode devriez-vous utiliser ?

L’arbre de décision suivant vous aide à décider quel test post-hoc vous devez utiliser en fonction de la situation :

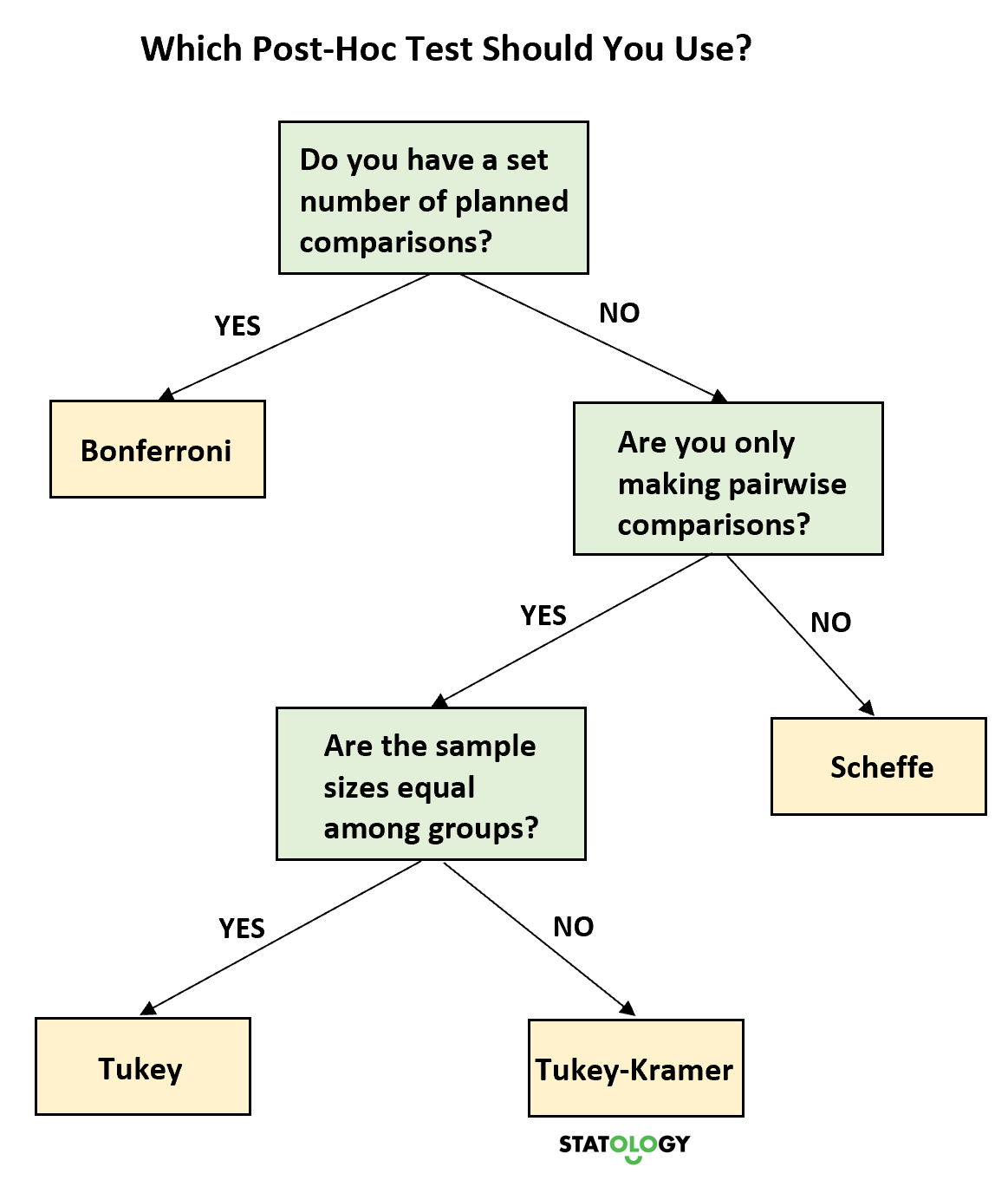
Pensées finales

Quel que soit le test post-hoc que vous choisissez d’utiliser, vous devez en décider avant de mener l’expérience.

Cela vous évite de choisir un test post-hoc après l’expérience qui serait plus susceptible de produire des résultats significatifs, ce qui est considéré comme une pratique malhonnête en recherche.

Quoi qu’il en soit, la plupart des logiciels statistiques sont capables d’effectuer ces tests post-hoc, vous aurez donc rarement besoin de les calculer manuellement.