Types d’asymétrie

Par Pr Amélia Rodriguez août 5, 2023 Statistiques 0 commentaire

Dans cet article, vous découvrirez combien de types d’asymétrie existent dans les statistiques. Ainsi, chaque type d’asymétrie est expliqué avec des exemples et, en plus, vous pourrez voir comment est calculée l’asymétrie d’une distribution.

Quels sont les types d’asymétrie ?

En statistique, il existe trois types d’asymétrie :

Asymétrie positive : La distribution a plus de valeurs différentes à droite de la moyenne qu’à gauche.
Asymétrie négative : La distribution a plus de valeurs différentes à gauche de la moyenne qu’à sa droite.
Symétrie : La distribution a le même nombre de valeurs à gauche et à droite de la moyenne.

Chaque type d’asymétrie est expliqué plus en détail ci-dessous.

asymétrie positive

Lorsqu’une distribution a une asymétrie positive , cela signifie que son graphique a la queue droite plus longue que la queue gauche. C’est-à-dire que la distribution a des valeurs plus différentes à droite de la moyenne.

La courbe de l’exemple précédent est positivement asymétrique car il y a beaucoup plus de valeurs à droite de la moyenne qu’à gauche. Comme vous pouvez le voir sur le graphique, la barre représentée en vert est beaucoup plus grande que la barre orange.

asymétrie négative

En statistiques, on dit qu’une distribution a une asymétrie négative lorsque son graphique a la queue gauche plus longue que la queue droite. Autrement dit, une distribution négativement asymétrique signifie qu’elle a des valeurs plus différentes à gauche de la moyenne.

Si vous regardez le graphique précédent, il y a plus de valeurs à gauche de la moyenne qu’à droite, donc la courbe est négativement asymétrique.

Symétrie

Une distribution est symétrique lorsque le nombre de valeurs à gauche de la moyenne est égal au nombre de valeurs à droite de la moyenne. La moyenne fait donc office d’axe de symétrie.

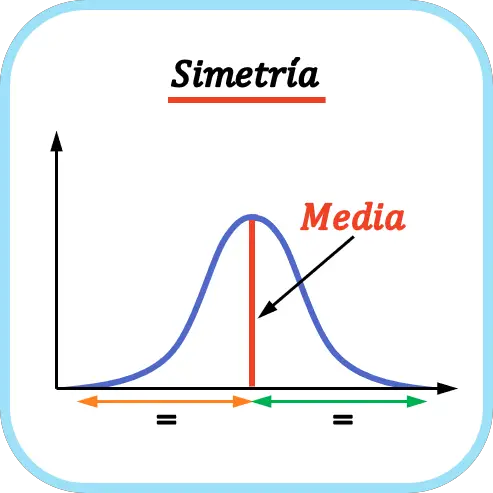
Comme le montre l’exemple ci-dessus, le nombre de valeurs à gauche de la moyenne de la distribution de probabilité représentée coïncide avec le nombre de valeurs à droite de la moyenne, c’est donc une distribution symétrique.

Comment déterminer le type d’asymétrie

Maintenant que nous savons quels sont les différents types d’asymétrie en statistique, voyons comment savoir à quel type d’asymétrie correspond une distribution de probabilité.

Traditionnellement, on explique que l’on peut connaître le type d’asymétrie d’une distribution en fonction de la relation entre sa moyenne et sa médiane (si elle est plus grande, équivalente ou plus petite). Cependant, cette propriété n’est pas toujours satisfaite. Ainsi, pour déterminer l’asymétrie d’une distribution, le coefficient d’asymétrie de Fisher doit être calculé.

Le coefficient d’asymétrie de Fisher est calculé à l’aide de la formule suivante :

$\displaystyle\gamma_1=E\left[\left(\frac{X-\mu}{\sigma}\right)^3 \right]$

Ou équivalent:

$\displaystyle\gamma_1=\frac{\operatorname{E}[X^3] - 3\mu\sigma^2 - \mu^3}{\sigma^3}$

Où

$E$ est l’ espérance mathématique , $\mu$ la moyenne arithmétique et $\sigma$ l’ écart type .

Et une fois le coefficient de Fisher calculé, son signe permet de déterminer quel type d’asymétrie présente la distribution :

Si le coefficient d’asymétrie de Fisher est positif, la distribution est positivement asymétrique.
Si le coefficient d’asymétrie de Fisher est négatif, la distribution est asymétrique négativement.
Si la distribution est symétrique, le coefficient d’asymétrie de Fisher est égal à zéro (l’inverse n’est pas toujours vrai).

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus