Typification

Cet article explique ce que signifie caractériser une distribution dans les statistiques. Ainsi, vous trouverez la définition de la typification, un exemple de typification d’une variable et, en plus, vous pourrez vous entraîner avec un exercice résolu étape par étape.

Qu’est-ce que taper ?

En statistique, la normalisation est un processus dans lequel une transformation linéaire est appliquée à une distribution de sorte que sa moyenne et son écart type soient respectivement égaux à zéro et un.

Plus précisément, le typage consiste à soustraire la moyenne de la variable aléatoire puis à la diviser par l’écart type.

La saisie peut également être appelée normalisation ou standardisation.

Formule de saisie

Pour classer une variable, vous devez soustraire sa moyenne puis la diviser par son écart type. La formule pour saisir une variable est donc la suivante :

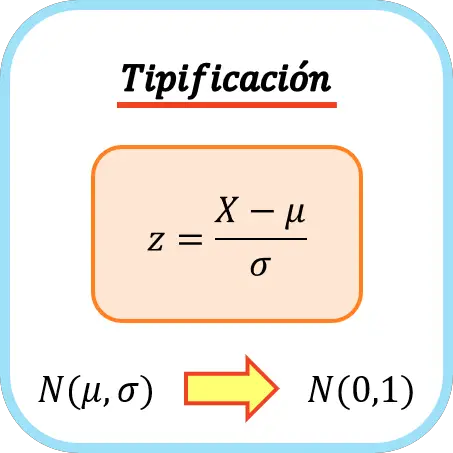
Où

est la moyenne de la variable et son écart type (ou écart type).

Par conséquent, la saisie est en fait un changement de variable, puisqu’une transformation linéaire est appliquée à la variable.

Exemple de saisie

Compte tenu de la définition de la typification et de sa formule, vous trouverez ci-dessous un exemple concret pour bien comprendre le concept.

• Une variable aléatoire continue suit une loi normale de moyenne 45 et d’écart type 10, quelle est la probabilité d’obtenir une valeur inférieure ou égale à 60 ?

Pour trouver la probabilité d’une distribution normale, nous devons utiliser sa table caractéristique, mais pour ce faire, nous devons d’abord effectuer le processus de typage. Nous soustrayons donc la moyenne et divisons par l’écart type à la valeur de probabilité :

Une fois que nous avons standardisé, nous passons au tableau de probabilité de la distribution normale pour voir à quelle probabilité correspond la valeur de 1,5 :

Comme on peut le voir dans le tableau de typification de la distribution normale, la valeur calculée à l’étape précédente correspond à la probabilité suivante :

La probabilité d’obtenir une valeur égale ou inférieure à 60 est donc de 93,32 %.

Exercice de frappe résolu

Calculez les probabilités suivantes d’une distribution normale dont la moyenne et l’écart type sont respectivement de 120 et 50.

• La probabilité d’obtenir une valeur inférieure ou égale à 208.
• La probabilité d’obtenir une valeur supérieure à 137.

Dans les deux sections du problème, nous devons taper la distribution normale pour calculer les probabilités.

On commence par calculer le typage de la probabilité d’une valeur inférieure ou équivalente à 208 :

Et maintenant, regardons le tableau ci-dessus à quelle probabilité correspond la valeur 1,76 :

Dans un deuxième temps, nous allons calculer la probabilité d’obtenir une valeur supérieure à 137. De la même manière, nous commençons par taper la variable :

Cependant, le tableau ci-joint n’a que les probabilités cumulées les plus faibles, donc pour utiliser le tableau, nous devons d’abord transformer la probabilité :

Et, enfin, on retiendra du tableau ci-joint la probabilité correspondant à la valeur calculée de Z :

A quoi sert de taper ?

Pour finir de comprendre le sens de la typification, nous allons voir à quoi elle sert et quand une variable doit être typée.

Principalement, la standardisation est utilisée pour comparer les valeurs de distributions avec des moyennes et des variances différentes. De même, la standardisation est également utilisée pour calculer une probabilité.

En standardisant deux valeurs de distributions ayant des caractéristiques différentes, nous pouvons voir quelle valeur est plus grande ou plus petite par rapport à l’ensemble de la distribution. Ou en d’autres termes, en appliquant le processus de typification, nous pouvons voir quelle valeur est la plus proche ou la plus éloignée de la moyenne de sa distribution.

De plus, comme expliqué ci-dessus, la typification permet également le calcul de probabilités, puisque généralement les tableaux de probabilités sont basés sur une distribution typifiée.