Comment effectuer un test t sur un échantillon dans Excel

Un test t sur un échantillon est utilisé pour tester si la moyenne d’une population est égale ou non à une certaine valeur.

Ce didacticiel explique comment effectuer un test t sur un échantillon dans Excel.

Comment effectuer un test t sur un échantillon dans Excel

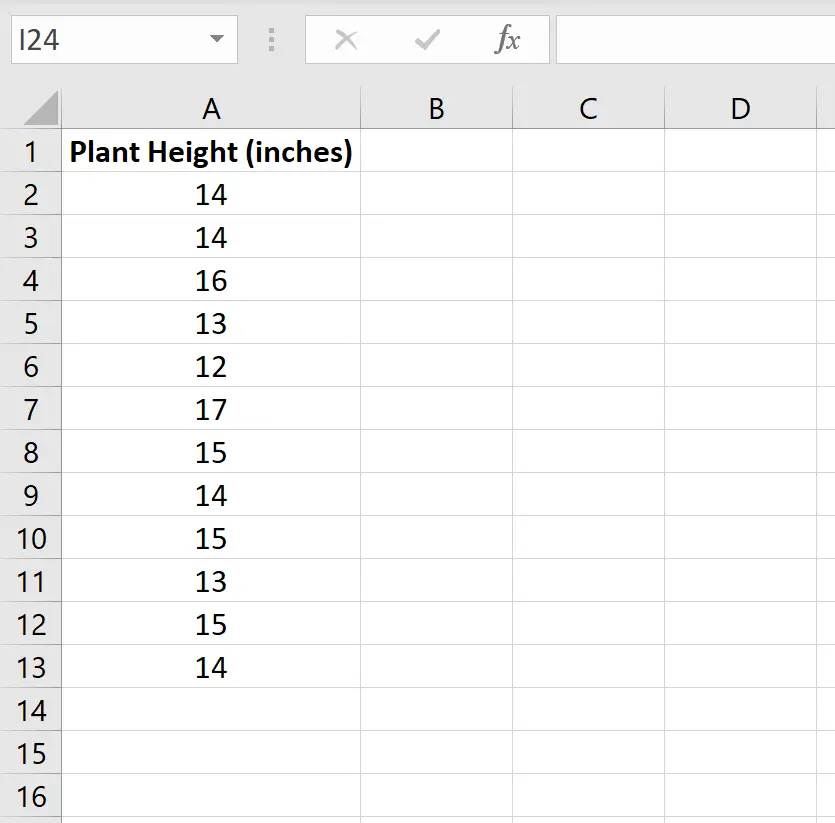
Supposons qu’un botaniste veuille savoir si la hauteur moyenne d’une certaine espèce de plante est égale à 15 pouces. Elle prélève un échantillon aléatoire de 12 plantes et enregistre chacune de leurs hauteurs en pouces.

L’image suivante montre la hauteur (en pouces) de chaque plante de l’échantillon :

Nous pouvons utiliser les étapes suivantes pour effectuer un test t sur un échantillon afin de déterminer si la hauteur moyenne de cette espèce de plante est réellement égale à 15 pouces.

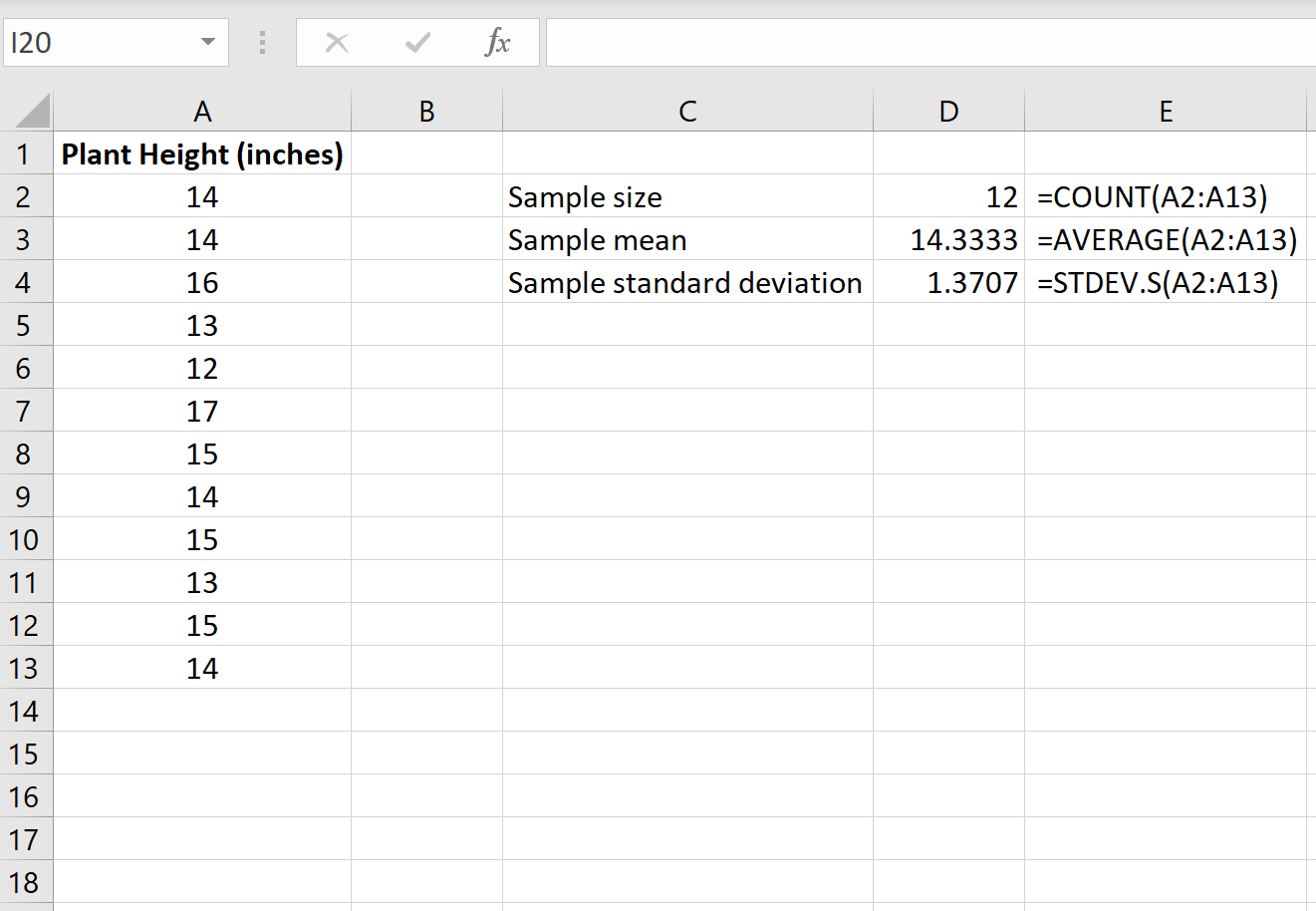
Étape 1 : Recherchez la taille de l’échantillon, la moyenne de l’échantillon et l’écart type de l’échantillon.

Tout d’abord, nous devons trouver la taille de l’échantillon, la moyenne de l’échantillon et l’écart type de l’échantillon, qui seront tous utilisés pour effectuer le test t sur un échantillon.

L’image suivante montre les formules que nous pouvons utiliser pour calculer ces valeurs :

Étape 2 : Calculez la statistique de test t .

Ensuite, nous calculerons la statistique de test t en utilisant la formule suivante :

t = x – µ / (s/√ n )

où:

x = moyenne de l’échantillon

µ = moyenne hypothétique de la population

s = écart type de l’échantillon

n = taille de l’échantillon

L’image suivante montre comment calculer t dans Excel :

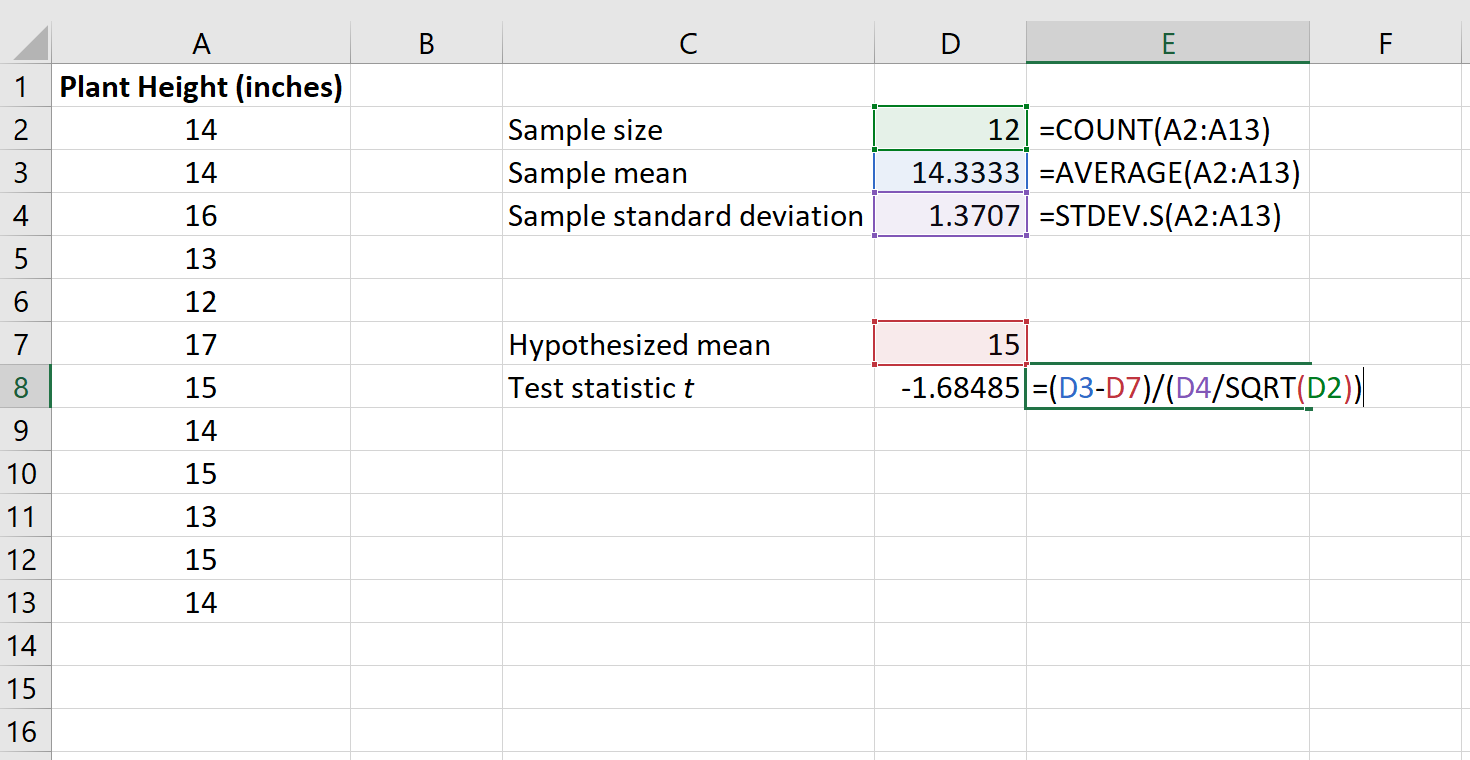
La statistique de test t s’avère être -1,68485 .

Étape 3 : Calculez la valeur p de la statistique de test.

Ensuite, nous devons calculer la valeur p associée à la statistique de test à l’aide de la fonction suivante dans Excel :

=T.DIST.2T(ABS(x), deg_liberté)

où:

x = statistique de test t

deg_freedom = degrés de liberté pour le test, calculés comme n-1

Notes techniques :

La fonction T.DIST.2T() renvoie la valeur p pour un test t bilatéral. Si vous effectuez plutôt un test t gauche ou droit, vous utiliserez plutôt les fonctions T.DIST() ou T.DIST.RT() , respectivement.

L’image suivante montre comment calculer la valeur p pour notre statistique de test :

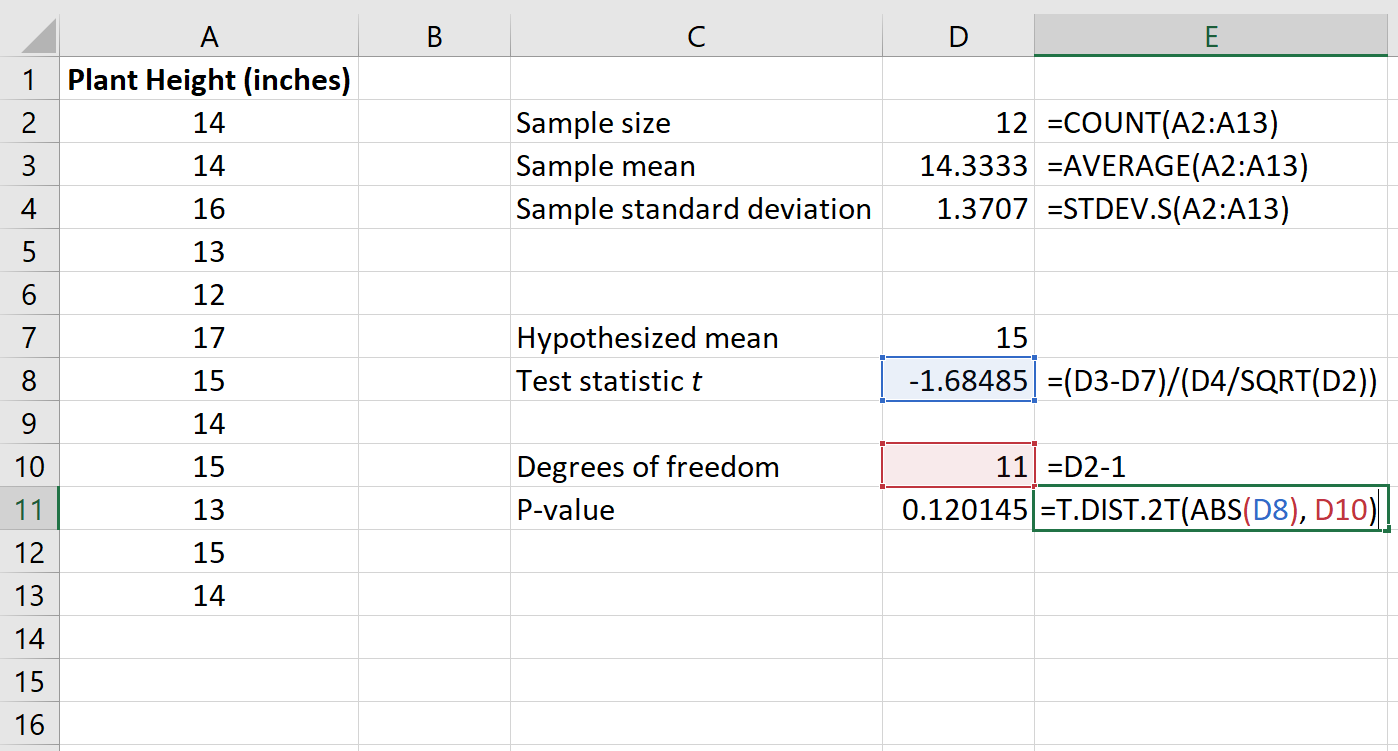
La valeur p s’avère être de 0,120145 .

Étape 4 : Interprétez les résultats.

Les deux hypothèses pour ce test t sur un échantillon particulier sont les suivantes :

H ₀ : µ = 15 (la hauteur moyenne de cette espèce de plante est de 15 pouces)

H _A : µ ≠15 (la hauteur moyenne n’est pas de 15 pouces)

La valeur p de notre test (0,120145) étant supérieure à alpha = 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle du test.

Nous ne disposons pas de preuves suffisantes pour affirmer que la hauteur moyenne de cette espèce particulière de plante est différente de 15 pouces.

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres types courants de tests t dans Excel :

Comment effectuer un test t à deux échantillons dans Excel
Comment effectuer un test t pour échantillons appariés dans Excel