Comment effectuer un test t sur un échantillon dans Stata

Un test t sur un échantillon est utilisé pour tester si la moyenne d’une population est égale ou non à une certaine valeur.

Ce didacticiel explique comment effectuer un test t sur un échantillon dans Stata.

Exemple : test t sur un échantillon dans Stata

Les chercheurs veulent savoir si les automobiles parcourent en moyenne 20 miles par gallon. Ils collectent un échantillon de 74 voitures et souhaitent effectuer un test T sur un échantillon pour déterminer si le véritable mpg moyen est de 20 ou non.

Effectuez les étapes suivantes pour effectuer un test t sur un échantillon.

Étape 1 : Chargez les données.

Tout d’abord, chargez les données en tapant use https://www.stata-press.com/data/r13/auto dans la zone de commande et en cliquant sur Entrée.

Étape 2 : Affichez les données brutes.

Avant d’effectuer un test t sur un échantillon, examinons d’abord les données brutes. Dans la barre de menu supérieure, accédez à Données > Editeur de données > Editeur de données (Parcourir) . Cela nous montrera un tas d’informations sur chacune des 74 voitures, mais gardez à l’esprit que nous ne nous intéressons qu’aux miles par gallon (la colonne mpg ) :

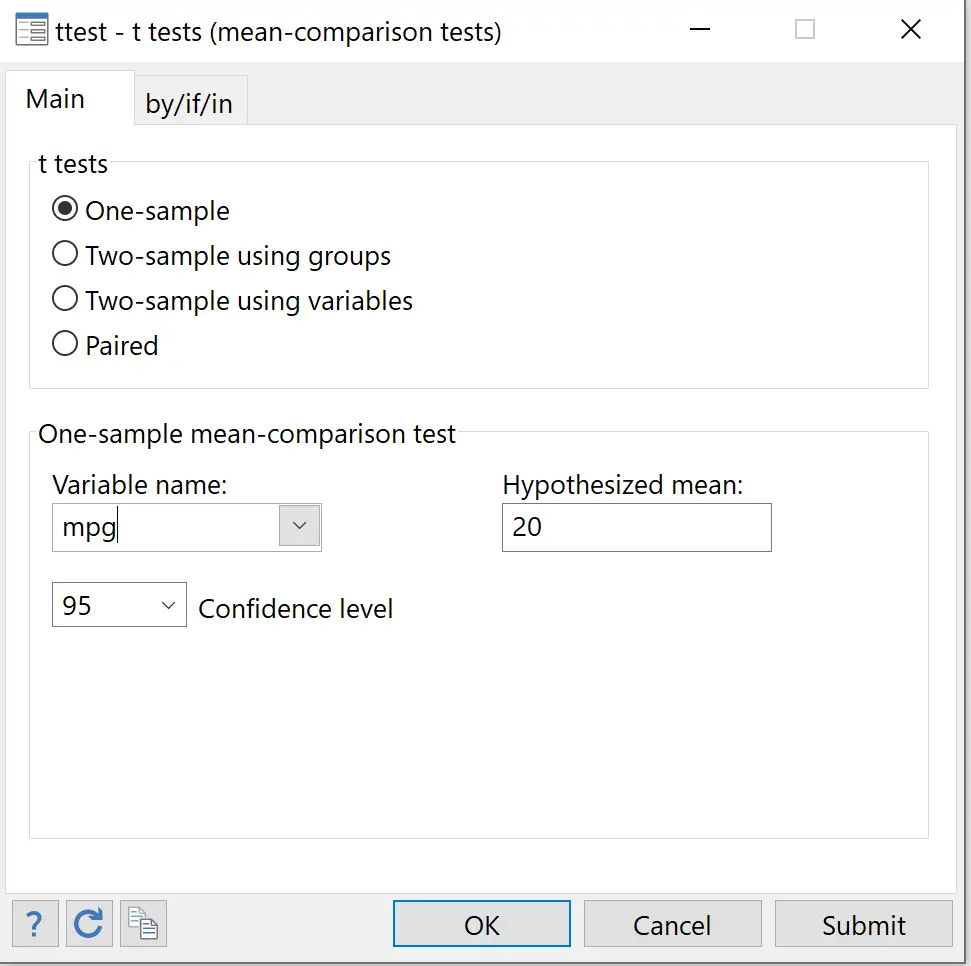
Étape 3 : Effectuez un test t sur un échantillon.

Dans la barre de menu supérieure, accédez à Statistiques > Résumés, tableaux et tests > Tests classiques d’hypothèses > Test t (test de comparaison de moyennes) .

Gardez un échantillon sélectionné. Pour Nom de la variable, choisissez mpg . Pour Moyenne hypothétique, saisissez 20 . Pour Niveau de confiance, choisissez le niveau de votre choix. Une valeur de 95 correspond à un niveau de signification de 0,05. Nous laisserons cela à 95. Enfin, cliquez sur OK .

Les résultats du test t sur un échantillon seront affichés :

Voici comment interpréter les résultats :

Obs : Le nombre d’observations. Dans ce cas, il y a 74 voitures au total.

Moyenne : le mpg moyen de toutes les voitures. Dans ce cas, la moyenne est de 21,2973 milles par gallon.

Norme. Err : calculé comme σ / √ n = 5,785503 / √ 74 = 0,6725511.

Norme. Dev : l’écart type de mpg. Dans ce cas, il s’agit de 5,785503.

95% Conf. Intervalle : intervalle de confiance à 95 % pour la véritable moyenne de la population.

t : La statistique de test, calculée comme (x – u) / (σ / √ n )= (21,2973-20) / 5,785503 / √ 74 = 1,9289.

degrés de liberté : degrés de liberté à utiliser pour le test t, calculés comme n-1 = 74-1 = 73.

Les valeurs p pour trois tests t différents sur un échantillon sont affichées au bas des résultats. Puisque nous souhaitons comprendre si le vrai mpg moyen est de 20 ou non, nous examinerons les résultats du test intermédiaire (dans lequel l’hypothèse alternative est Ha : moyenne !=20) qui a une valeur p de 0,0576 .

Puisque cette valeur n’est pas inférieure à notre seuil de signification de 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle. Nous n’avons pas suffisamment de preuves pour affirmer que le véritable mpg moyen pour cette population de voitures est différent de 20 mpg.

Étape 4 : Rapportez les résultats.

Enfin, nous rapporterons les résultats de notre test t sur un échantillon. Voici un exemple de la façon de procéder :

Un test t sur un échantillon a été effectué sur 74 voitures pour déterminer si le mpg moyen réel de la population était différent de 20 mpg.

Les résultats ont montré que la moyenne réelle de la population n’était pas différente de 20 mpg (t = 1,9289 avec df = 73, p = 0,0576) à un niveau de signification de 0,05.

Un intervalle de confiance de 95 % pour la moyenne réelle de la population a donné l’intervalle de (19,9569, 22,63769).