Un Z-Score peut-il être négatif ?

En statistiques, un score z nous indique à combien d’écarts types une valeur se trouve par rapport à la moyenne . Nous utilisons la formule suivante pour calculer un z-score :

z = (X – μ) / σ

où X est la valeur que nous analysons, μ est la moyenne et σ est l’écart type.

Un score z peut être positif, négatif ou égal à zéro.

Un score z positif indique qu’une valeur particulière est supérieure à la moyenne, un score z négatif indique qu’une valeur particulière est inférieure à la moyenne et un score z de zéro indique qu’une valeur particulière est égale à la moyenne.

Quelques exemples devraient le montrer clairement.

Exemples : Calcul d’un score Z

Supposons que nous ayons l’ensemble de données suivant qui montre la hauteur (en pouces) d’un certain groupe de plantes :

5, 7, 7, 8, 9, 10, 13, 17, 17, 18, 19, 19, 20

La moyenne de l’échantillon de cet ensemble de données est de 13 et l’écart type de l’échantillon est de 5,51 .

1. Recherchez le score z pour la valeur « 8 » dans cet ensemble de données.

Voici comment calculer le z-score :

z = (X – μ) / σ = (8 – 13) / 5,51 = -0,91

Cela signifie que la valeur « 8 » est inférieure de 0,91 écart-type à la moyenne.

2. Recherchez le score z pour la valeur « 13 » dans cet ensemble de données.

Voici comment calculer le z-score :

z = (X – μ) / σ = (13 – 13) / 5,46 = 0

Cela signifie que la valeur « 13 » est exactement égale à la moyenne.

3. Recherchez le score z pour la valeur « 20 » dans cet ensemble de données.

Voici comment calculer le z-score :

z = (X – μ) / σ = (20 – 13) / 5,46 = 1,28

Cela signifie que la valeur « 20 » est 1,28 écart-type au-dessus de la moyenne.

Comment interpréter les scores Z

Un tableau Z nous indique quel pourcentage de valeurs tombent en dessous de certains scores Z. Quelques exemples devraient le montrer clairement.

Exemple 1 : scores Z négatifs

Plus tôt, nous avons constaté que la valeur brute « 8 » dans notre ensemble de données avait un score z de -0,91 . Selon la table Z, 18,14 % des valeurs sont inférieures à cette valeur.

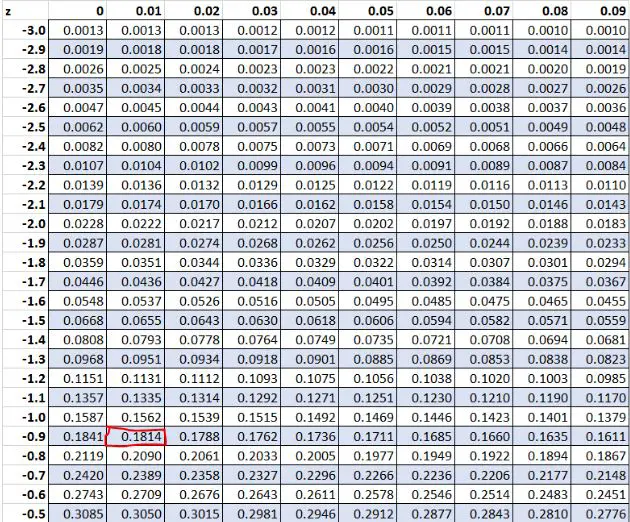
Exemple 2 : Z-Scores égaux à zéro

Plus tôt, nous avons constaté que la valeur brute « 13 » dans notre ensemble de données avait un score z de 0 . Selon la table Z, 50,00 % des valeurs sont inférieures à cette valeur.

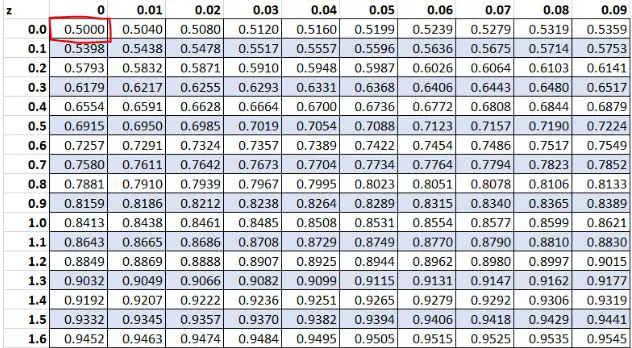
Exemple 3 : scores Z positifs

Plus tôt, nous avons constaté que la valeur brute « 20 » dans notre ensemble de données avait un score z de 1,28 . Selon la table Z, 89,97 % des valeurs sont inférieures à cette valeur.

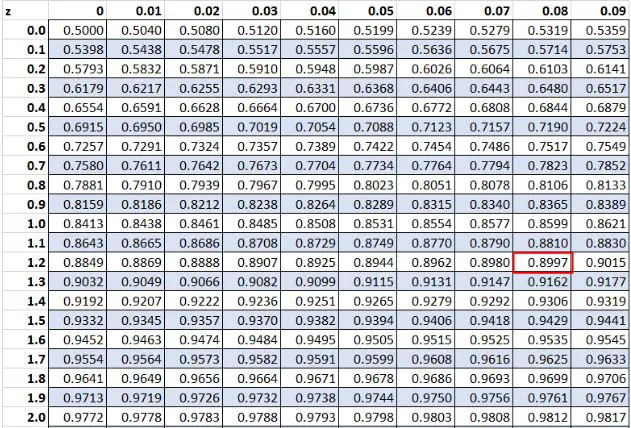
Conclusion

Les scores Z peuvent prendre n’importe quelle valeur comprise entre l’infini négatif et l’infini positif, mais la plupart des scores z se situent à moins de 2 écarts types de la moyenne. Il existe en fait une règle dans les statistiques connue sous le nom de règle empirique , qui stipule que pour un ensemble de données donné avec une distribution normale :

• 68 % des valeurs des données se situent dans un écart type de la moyenne.
• 95 % des valeurs des données se situent à moins de deux écarts types de la moyenne.
• 99,7 % des valeurs des données se situent dans trois écarts types de la moyenne.

Plus la valeur absolue d’un score z est élevée, plus une valeur brute est éloignée de la moyenne de l’ensemble de données. Plus la valeur absolue d’un score z est faible, plus une valeur brute est proche de la moyenne de l’ensemble de données.

Rubriques connexes:

Calculateur de règles empiriques
Comment appliquer la règle empirique dans Excel