Valeur critique

Par Pr Amélia Rodriguez août 3, 2023 Statistiques 0 commentaire

Cet article explique quelle est la valeur critique en statistique et comment elle doit être interprétée dans un test d’hypothèse. De même, vous pourrez voir comment la valeur critique est calculée ainsi que plusieurs exemples concrets.

Qu’est-ce que la valeur critique ?

La valeur critique est le point de la distribution de la statistique de test qui sépare la région de rejet de l’hypothèse nulle de sa région d’acceptation. Autrement dit, la valeur critique est la valeur de la distribution du test statistique qui marque la limite de la région de rejet (ou région critique).

Normalement, la valeur critique est représentée par le symbole Z _α/2 , puisque la distribution de référence la plus courante est généralement la distribution normale standard .

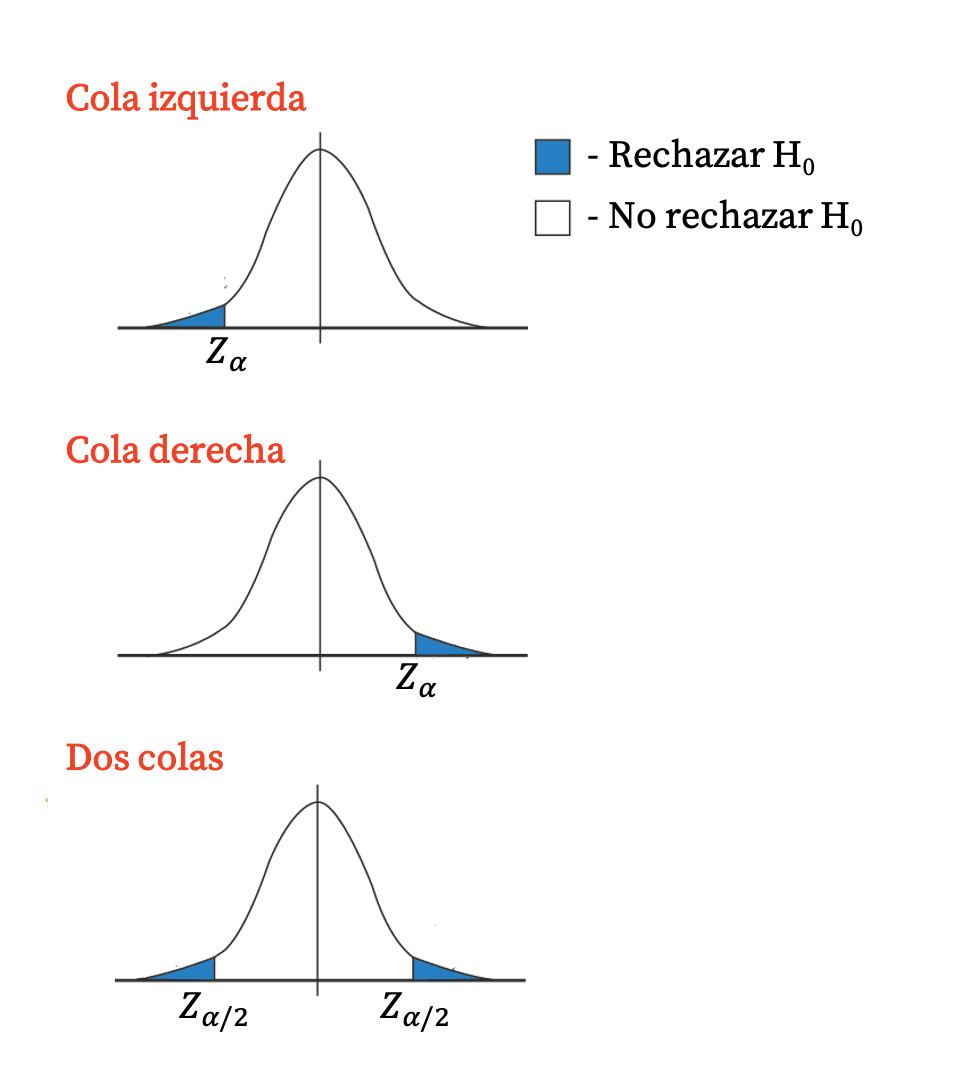
En général, les tests unilatéraux ont une valeur critique, puisque la région de rejet constitue une seule queue de la distribution. D’un autre côté, les tests bilatéraux ont deux valeurs critiques, car la région de rejet correspond aux deux queues de la distribution.

Dans les intervalles de confiance , les valeurs critiques sont les points de la distribution de référence qui marquent les limites de l’intervalle de confiance.

Comment calculer la valeur critique

Nous verrons ensuite comment sont calculées les valeurs critiques les plus courantes. La valeur critique de Z et la valeur critique de t sont calculées pour l’intervalle de confiance de la moyenne, la seule différence est que la valeur critique de Z est calculée lorsque l’écart type de la population est connu, et à la place la valeur critique de t est utilisé lorsque seules les données d’un échantillon sont connues.

Valeur critique de Z

La valeur critique de Z est utilisée pour déterminer les limites de l’intervalle de confiance pour la moyenne. Plus précisément, il n’est utilisé que si vous connaissez l’écart type de la population.

Pour calculer la valeur critique de Z, la valeur correspondant à la probabilité de la moitié du niveau de signification doit être trouvée dans le tableau de la distribution normale standard .

Par exemple, si l’on veut déterminer un intervalle de confiance pour la moyenne avec un niveau de confiance de 95 %, cela implique que le niveau de signification est de 5 %. Par conséquent, il faut voir dans le tableau de la distribution normale standard quelle valeur correspond à une probabilité de 2,5%, puisque l’intervalle de confiance pour la moyenne est bilatéral.

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}$

Ci-dessous vous pouvez voir un tableau avec les valeurs critiques de Z les plus utilisées :

Niveau de confiance (1-α)	Niveau de signification (α)	Valeur critique (Z _α/2 )
0,80	0,20	1 282
0,85	0,15	1 440
0,90	0,10	1 645
0,95	0,05	1960
0,99	0,01	2 576
0,995	0,005	2 807
0,999	0,001	3 291

Valeur critique de t

La valeur t critique est utilisée pour trouver les limites de l’intervalle de confiance pour la moyenne lorsque l’écart type de la population est inconnu.

Pour calculer la valeur critique de t, la valeur correspondant à la probabilité de la moitié du niveau de signification doit être trouvée dans la table de distribution t de Student , en tenant compte du fait que les degrés de liberté de la distribution t de Student sont d’une unité. que la taille de l’échantillon.

Par exemple, si nous voulons trouver l’intervalle de confiance avec un niveau de confiance de 95 % et que la taille de l’échantillon est de 8, nous devons accéder à la table de distribution t de Student et voir quelle valeur correspond à t _0,025|7 .

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 7}=2,365\end{array}$

➤ Voir : Comment calculer l’intervalle de confiance de la moyenne

La valeur critique dans les tests d’hypothèses

La valeur critique peut également être utilisée dans les tests d’hypothèse pour rejeter l’hypothèse nulle (et accepter l’hypothèse alternative) ou rejeter l’hypothèse alternative (et accepter l’hypothèse nulle).

Si la valeur de la distribution de la statistique de test correspondant à la valeur p se situe dans l’intervalle marqué par les valeurs critiques, l’hypothèse nulle n’est pas rejetée (l’hypothèse alternative est rejetée).
Si la valeur de la distribution de la statistique de test correspondant à la p-value est en dehors de l’intervalle marqué par les valeurs critiques, l’hypothèse nulle est rejetée (l’hypothèse alternative est acceptée).

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus