La différence entre les valeurs Z et les valeurs P dans les statistiques

Deux termes que les étudiants confondent souvent dans les statistiques sont les valeurs z et les valeurs p .

Pour comprendre la différence entre ces termes, il est utile de comprendre les tests z .

Il existe deux types courants de tests z :

• Test z à un échantillon : utilisé pour tester si une moyenne de population est égale à une certaine valeur.
• Test z à deux échantillons : utilisé pour tester si deux moyennes de population sont égales.

Nous utilisons les étapes suivantes pour effectuer chaque test :

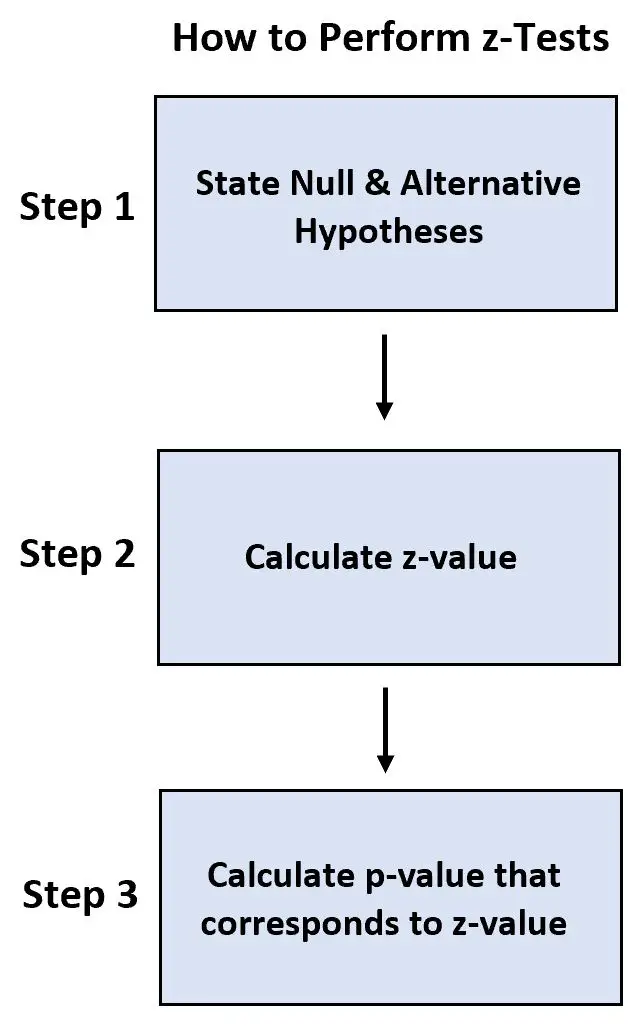
• Étape 1 : Énoncez l’hypothèse nulle et alternative.
• Étape 2 : Calculez la valeur z.
• Étape 3 : Calculez la valeur p qui correspond à la valeur z.

Pour chaque test, la valeur z est un moyen de quantifier la différence entre les moyennes de la population et la valeur p est la probabilité d’obtenir une valeur z avec une valeur absolue au moins aussi grande que celle que nous avons réellement observée dans l’échantillon. données si l’hypothèse nulle est réellement vraie.

Si la valeur p est inférieure à une certaine valeur (par exemple 0,05), alors nous rejetons l’hypothèse nulle du test.

Pour chaque type de test z, nous nous intéressons à la valeur p et nous utilisons simplement la valeur z comme étape intermédiaire pour calculer la valeur p.

L’exemple suivant montre comment calculer et interpréter une valeur z et la valeur p correspondante pour un test z à deux échantillons.

Exemple : calculer et interpréter les valeurs Z et les valeurs P

Supposons que les niveaux de QI des individus de deux villes différentes soient normalement distribués, chacun avec des écarts types de population de 15.

Une scientifique veut savoir si le niveau de QI moyen entre les individus de la ville A et de la ville B est différent. Elle sélectionne donc un échantillon aléatoire simple de 20 individus de chaque ville et enregistre leurs niveaux de QI :

Ville A : 82, 84, 85, 89, 91, 91, 92, 94, 99, 99, 105, 109, 109, 109, 110, 112, 112, 113, 114, 114

Ville B : 90, 91, 91, 91, 95, 95, 99, 99, 108, 109, 109, 114, 115, 116, 117, 117, 128, 129, 130, 133

Voici comment effectuer un test z sur deux échantillons en utilisant ces données :

Étape 1 : Énoncez l’hypothèse nulle et alternative.

Tout d’abord, nous énoncerons les hypothèses nulles et alternatives :

• H ₀ : μ ₁ = μ ₂ (les deux moyennes de population sont égales)
• H ₁ : μ ₁ ≠ μ ₂ (les deux moyennes de population ne sont pas égales)

Étape 2 : Calculez la valeur z.

Ensuite, nous effectuerons un test z sur deux échantillons dans Excel en utilisant ces données et constaterons que la valeur z est -1.71817 .

Étape 3 : Calculez la valeur p.

Nous pouvons utiliser lecalculateur de score Z vers valeur P pour constater que la valeur p qui correspond à une valeur z de -1,71817 est de 0,08577.

Puisque cette valeur p n’est pas inférieure à 0,05, nous ne disposons pas de preuves suffisantes pour rejeter l’hypothèse nulle.

Ainsi, nous concluons que le niveau de QI moyen n’est pas significativement différent entre les deux villes.

Notez que nous avons simplement utilisé la valeur z comme étape intermédiaire pour calculer la valeur p.

La valeur p est la vraie valeur qui nous intéressait, mais nous avons dû d’abord calculer la valeur z.

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer des tests z à l’aide de divers logiciels statistiques :

Comment effectuer des tests Z dans Excel
Comment effectuer des tests Z dans R
Comment effectuer des tests Z en Python