Valeurs atypiques (valeurs aberrantes)

Cet article explique ce que sont les valeurs aberrantes et comment elles sont calculées. De plus, vous pouvez calculer les valeurs aberrantes pour n’importe quel échantillon de données avec une calculatrice en ligne.

Que sont les valeurs aberrantes ?

En statistiques, les valeurs aberrantes , également appelées valeurs aberrantes ou valeurs aberrantes , sont des valeurs très différentes du reste de l’ensemble de données. Autrement dit, une valeur aberrante est une valeur anormale extrêmement différente du reste des valeurs de l’échantillon.

Il est important d’identifier les valeurs aberrantes dans un échantillon, car elles peuvent affecter considérablement le calcul des mesures statistiques.

Par exemple, si nous avons la série de données [1, 3, 5, 2, 79, 4, 8, 6], le nombre 79 est clairement une valeur aberrante. Parce que sa valeur est extrêmement supérieure au reste des données. Dans ce cas, la moyenne incluant la valeur aberrante est de 13,5, tandis que la moyenne sans la valeur aberrante serait de 4,14. Comme vous pouvez le constater, une seule valeur aberrante influence déjà de manière significative le résultat d’une mesure statistique.

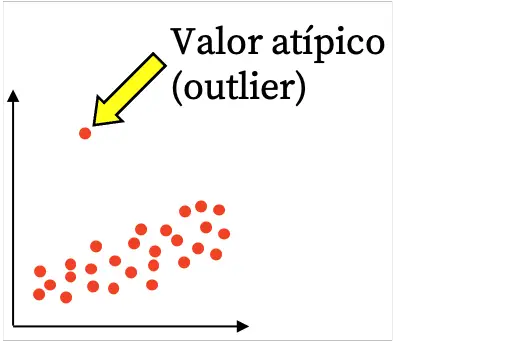
En règle générale, les valeurs aberrantes se distinguent facilement dans les nuages de points car elles sont isolées du reste des données. Regardez le nuage de points suivant, la valeur aberrante est très séparée du reste des valeurs :

👉 Vous pouvez utiliser la calculatrice ci-dessous pour trouver les valeurs aberrantes pour n’importe quel ensemble de données.

Comment calculer les valeurs aberrantes

Pour calculer les valeurs aberrantes d’un échantillon de données, les étapes suivantes doivent être suivies :

1. Calculez les quartiles de l’ensemble de données.
2. Calculez l’intervalle interquartile des données.
3. Les valeurs atypiques (valeurs aberrantes) seront considérées comme les valeurs qui remplissent l’une des conditions suivantes :
   • La valeur est inférieure au premier quartile moins 1,5 fois l’intervalle interquartile.

   

Par conséquent, afin de supprimer les valeurs aberrantes d’une distribution de probabilité, vous devez savoir comment les quartiles et l’intervalle interquartile d’un échantillon sont calculés. Si vous avez des questions, voici deux liens qui expliquent en détail comment procéder :

Dans le boxplot suivant, vous pouvez voir deux valeurs aberrantes selon ce critère représenté graphiquement :

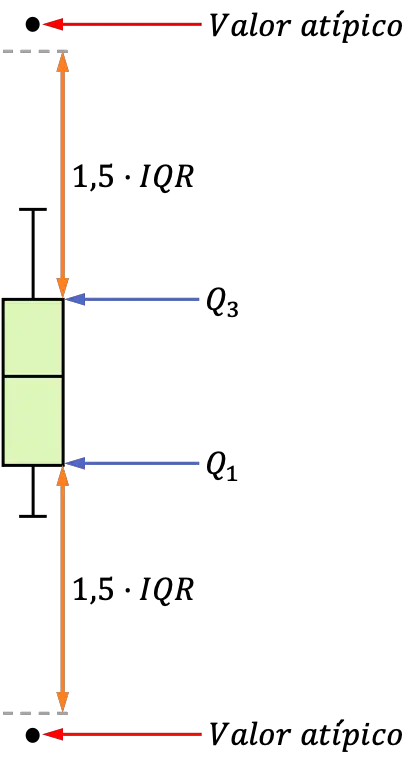
Remarque : Gardez à l’esprit qu’il existe plusieurs critères pour déterminer les limites au-delà desquelles les données sont considérées comme aberrantes. Dans cet article, le critère du test de Tukey a été pris comme référence, car il est le plus utilisé.

Exemple de valeurs aberrantes

Compte tenu de la définition d’une valeur aberrante, dans cette section, nous verrons un exemple pratique de la façon d’identifier les valeurs aberrantes dans une série de données.

• Calculez les valeurs atypiques ou aberrantes de l’ensemble de données statistiques suivant.

Tout d’abord, nous calculons les trois quartiles de l’ensemble de données :

Une fois que nous avons trouvé les trois quartiles, nous trouvons l’écart interquartile en soustrayant le quartile 3 moins le quartile 1 :

Et maintenant, nous calculons les limites fixées par les valeurs aberrantes. Pour ce faire, nous utilisons les formules expliquées dans la section ci-dessus :

Donc, si l’une des valeurs est inférieure à 3,16, il s’agit d’une valeur aberrante. De même, si une valeur est supérieure à 5,56, il s’agit également d’une valeur aberrante.

En conclusion, dans ce cas nous avons deux valeurs extrêmes, car 3,02 est inférieur à 3,16 et 5,71 est supérieur à 5,56.

Calculateur de valeurs aberrantes

Entrez un ensemble de données statistiques dans la calculatrice suivante pour calculer ses valeurs aberrantes, le cas échéant. Les données doivent être séparées par un espace et saisies en utilisant le point comme séparateur décimal.

Causes des valeurs aberrantes

Il existe plusieurs causes possibles aux valeurs aberrantes, dont les plus courantes sont :

• L’appareil utilisé pour effectuer les mesures est en panne ou a subi un accident.
• La pièce mesurée présentait un défaut dû à une cause anormale.
• Une erreur s’est produite dans la transmission ou la transcription des données.
• Il y a eu une erreur humaine. Quelles que soient les précautions prises, les erreurs humaines ne sont pas totalement inévitables et des valeurs anormales peuvent donc toujours exister.

Ce sont les causes les plus courantes, mais la raison peut évidemment être n’importe quoi. De même, il faut tenir compte du fait que lorsqu’une étude statistique est réalisée avec de nombreuses observations, il est normal que certaines valeurs aberrantes apparaissent.

Que faire des valeurs aberrantes

Une question courante lorsque nous rencontrons une valeur aberrante est de savoir que devons-nous en faire. Les valeurs aberrantes doivent-elles être supprimées de l’échantillon ?

On pense que les valeurs aberrantes devraient toujours être éliminées, car ce sont des données qui ne ressemblent pas au reste de l’ensemble. Cependant, même si les valeurs aberrantes affectent grandement les résultats de certaines mesures statistiques, cela ne signifie pas qu’elles doivent toujours être éliminées.

En général, les valeurs aberrantes ne doivent être supprimées que si nous savons que la cause de l’anomalie est véritablement justifiée et, par conséquent, ces valeurs aberrantes sont des observations qui ne correspondent pas à ce qui est étudié.

Ceci est particulièrement important dans les échantillons dont la taille est petite, car les valeurs extrêmes affectent alors davantage les métriques statistiques.

Par exemple, si la longueur d’une partie d’un produit est mesurée pour effectuer un contrôle qualité, logiquement si un autre type de produit apparaît soudainement et que la même partie est mesurée, la valeur mesurée sera très différente des précédentes et sera probablement être une valeur aberrante. Dans ce cas, la valeur aberrante pourrait être écartée car sa cause est connue et on sait que les données mesurées ne font pas partie de la population destinée à être analysée.