L’intervalle interquartile (IQR) est-il affecté par les valeurs aberrantes ?

En statistiques, nous souhaitons souvent savoir dans quelle mesure les valeurs sont « réparties » dans une distribution.

Un moyen populaire de mesurer la propagation est l’intervalle interquartile , qui est calculé comme la différence entre le premier quartile et le troisième quartile d’un ensemble de données. Les quartiles sont simplement des valeurs qui divisent un ensemble de données en quatre parties égales.

Exemple : Calcul de l’intervalle interquartile

L’exemple suivant montre comment calculer l’intervalle interquartile pour un ensemble de données donné :

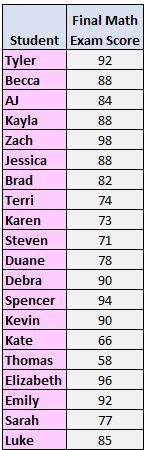
Étape 1 : Organisez les valeurs de la plus petite à la plus grande.

58, 66, 71, 73, 74, 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

2. Trouvez la médiane.

58, 66, 71, 73, 74, 77, 78, 82, 84, 85 , 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

Dans ce cas, la médiane se situe entre 85 et 88.

3. La médiane divise l’ensemble de données en deux moitiés. La médiane de la moitié inférieure est le quartile inférieur et la médiane de la moitié supérieure est le quartile supérieur :

58, 66, 71, 73 , 74 , 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94 , 96, 98

4. Calculez l’intervalle interquartile.

Dans ce cas, le premier quartile est la moyenne des deux valeurs du milieu dans la moitié inférieure de l’ensemble de données (75,5) et le troisième quartile est la moyenne des deux valeurs du milieu dans la moitié supérieure de l’ensemble de données (91).

Ainsi, l’intervalle interquartile est de 91 – 75,5 = 15,5

L’intervalle interquartile n’est pas affecté par les valeurs aberrantes

L’une des raisons pour lesquelles les gens préfèrent utiliser l’intervalle interquartile (IQR) lors du calcul de la « propagation » d’un ensemble de données est qu’il résiste aux valeurs aberrantes. Étant donné que l’IQR correspond simplement à la plage des 50 % moyens des valeurs des données, il n’est pas affecté par les valeurs aberrantes extrêmes .

Pour démontrer cela, considérons l’ensemble de données suivant :

[1, 4, 8, 11, 13, 17, 17, 20]

Voici les différentes mesures de propagation pour cet ensemble de données :

• Écart interquartile : 11
• Portée : 19
• Écart type : 6,26
• Écart : 39,23

Considérons maintenant le même ensemble de données mais avec une valeur aberrante extrême ajoutée :

[1, 4, 8, 11, 13, 17, 17, 20, 150 ]

Voici les différentes mesures de propagation pour cet ensemble de données :

• Écart interquartile : 12,5
• Portée : 149
• Écart type : 43,96
• Écart : 1 932,84

Remarquez comment l’écart interquartile ne change que légèrement, de 11 à 12,5. Cependant, toutes les autres mesures de dispersion changent radicalement.

Cela démontre que l’écart interquartile n’est pas affecté par les valeurs aberrantes comme les autres mesures de dispersion. Pour cette raison, il s’agit d’un moyen fiable de mesurer la répartition des 50 % moyens des valeurs dans n’importe quelle distribution.

Lectures complémentaires :

Mesures de dispersion
Calculateur d’intervalle interquartile