Comment identifier les valeurs aberrantes dans SAS (avec exemple)

Une valeur aberrante est une observation anormalement éloignée des autres valeurs d’un ensemble de données. Les valeurs aberrantes peuvent poser problème car elles peuvent affecter les résultats d’une analyse.

La manière la plus courante d’identifier les valeurs aberrantes dans un ensemble de données consiste à utiliser l’intervalle interquartile.

L’intervalle interquartile (IQR) est la différence entre le 75e centile (Q3) et le 25e centile (Q1) dans un ensemble de données. Il mesure la répartition des 50 % moyens des valeurs.

Nous définissons généralement une observation comme étant aberrante si elle est 1,5 fois l’intervalle interquartile supérieur au troisième quartile (Q3) ou 1,5 fois l’intervalle interquartile inférieur au premier quartile (Q1).

Valeurs aberrantes = Observations > Q3 + 1,5*IQR ou < Q1 – 1,5*IQR

L’exemple suivant montre comment utiliser cette formule pour identifier les valeurs aberrantes dans un ensemble de données dans SAS.

Exemple : identification des valeurs aberrantes dans SAS

Supposons que nous ayons l’ensemble de données suivant dans SAS :

/*create dataset*/
data original_data;
    input team $ points;
    datalines;
A 18
B 24
C 26
D 34
E 38
F 45
G 48
H 54
I 60
J 73
K 79
L 85
M 94
N 98
O 221
P 223
;
run;

/*view dataset*/
proc print data=original_data;

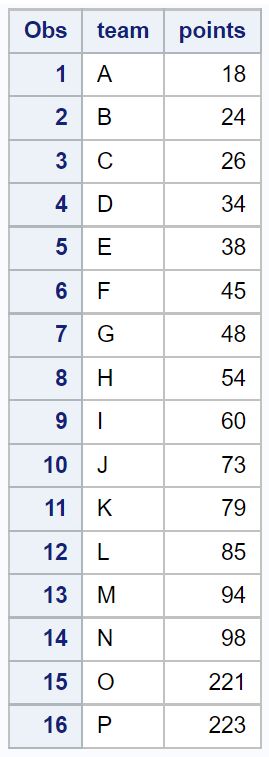
Le moyen le plus simple d’identifier les valeurs aberrantes dans SAS consiste à créer un boxplot, qui utilise automatiquement la formule mentionnée précédemment pour identifier et afficher les valeurs aberrantes dans l’ensemble de données sous forme de petits cercles :

/*create boxplot to visualize distribution of points*/
ods output sgplot=boxplot_data;
proc sgplot data=original_data;
    vbox points;
run;

/*view summary of boxplot descriptive statistics*/
proc print data=boxplot_data;

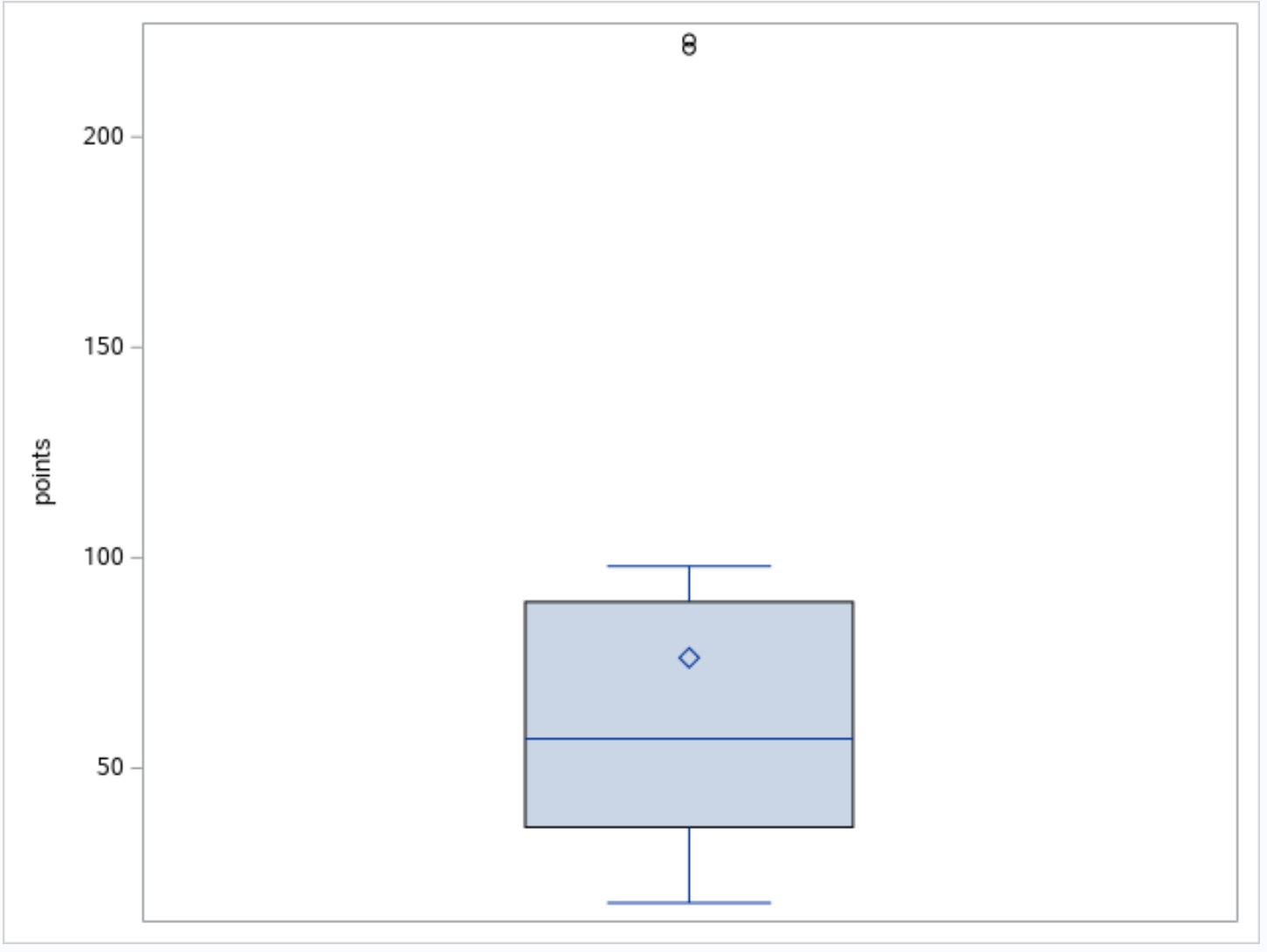
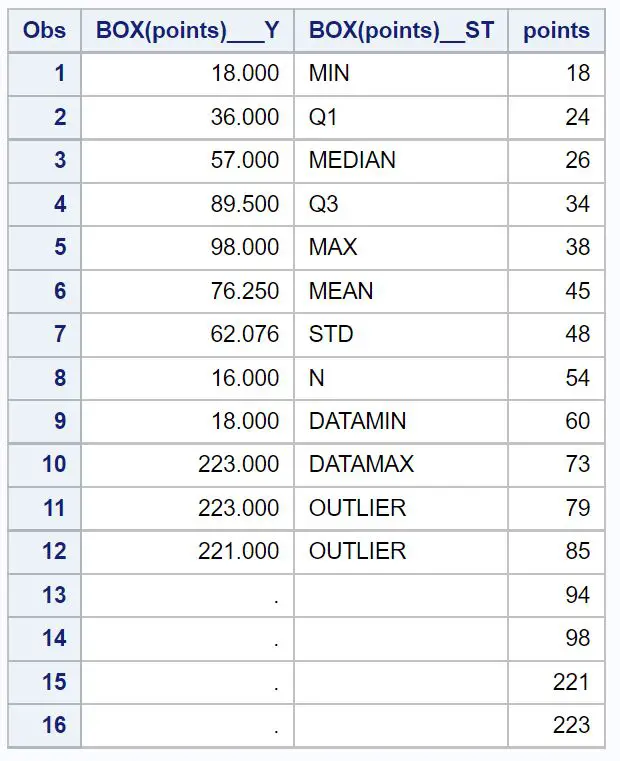
D’après le boxplot, nous pouvons voir qu’il y a deux petits cercles près du haut du tracé. Cela indique qu’il existe deux valeurs aberrantes.

Dans le tableau sous le boxplot, nous pouvons voir les valeurs exactes des deux valeurs aberrantes : 221 et 223 .

Nous pouvons vérifier manuellement que ces deux valeurs sont aberrantes en utilisant la formule précédente :

Valeurs aberrantes = Observations > Q3 + 1,5*IQR ou < Q1 – 1,5*IQR

L’intervalle interquartile est le suivant : Q3 – Q1 = 89,5 – 36 = 53,5.

La limite supérieure pour les valeurs aberrantes serait : Q3 + 1,5*IQR = 89,5 + 1,5*53,5 = 169,75.

Puisque 221 et 223 sont tous deux supérieurs à cette valeur, ils sont classés comme valeurs aberrantes.

Nous pourrions ensuite utiliser le code suivant pour supprimer ces deux valeurs aberrantes de l’ensemble de données si nous le souhaitons :

/*create new dataset with outliers removed*/
data new_data;
    set original_data;
    if points >= 221 then delete;
run;

/*view new dataset*/
proc print data=new_data;

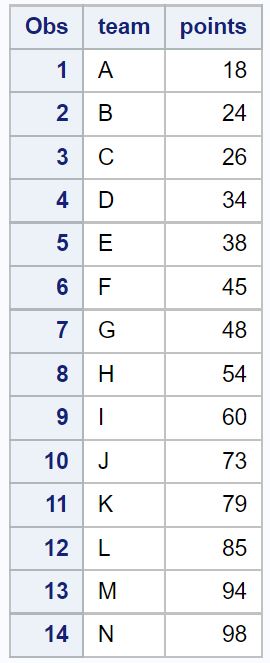
Notez que les deux valeurs aberrantes ont été supprimées.

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans SAS :

Comment utiliser le résumé de procédure dans SAS
Comment utiliser Proc Tabulate dans SAS
Comment calculer la corrélation dans SAS
Comment créer des tableaux de fréquences dans SAS
Comment remplacer les valeurs manquantes par zéro dans SAS