Variable dépendante et indépendante

Cet article explique ce que sont les variables dépendantes et indépendantes. Ainsi, vous découvrirez quelle est la différence entre une variable dépendante et une variable indépendante, comment savoir quelle est la variable dépendante et laquelle est indépendante et, en plus, plusieurs exemples de ce type de variable sont présentés.

Quelle est la variable dépendante et indépendante ?

La variable dépendante est la variable dont la valeur dépend d’une autre variable, qui est la variable indépendante . Par conséquent, la différence entre une variable dépendante et une variable indépendante est que la variable indépendante ne dépend d’aucune autre variable, mais que la variable dépendante dépend de la valeur de la variable indépendante.

Sur un graphique, la variable indépendante est représentée par la lettre x en abscisse (axe horizontal), tandis que la variable dépendante est représentée par la lettre y en ordonnée (axe vertical).

Par exemple, si dans une étude statistique on analyse la relation entre la note obtenue et les heures d’étude consacrées, les heures d’étude consacrées sont la variable indépendante et la note obtenue est la variable dépendante. Puisque la note obtenue dépend des heures étudiées, et non l’inverse.

Exemples de variables dépendantes et indépendantes

Dans la section précédente, nous avons vu la définition des variables dépendantes et indépendantes, nous allons donc maintenant voir dix exemples de ce type de variable pour mieux comprendre sa signification.

1. Le temps passé à étudier (variable indépendante) affecte les notes obtenues (variable dépendante).
2. Le prix d’un produit (variable indépendante) modifie le nombre de personnes prêtes à acheter le produit (variable dépendante).
3. La santé d’une personne (variable dépendante) dépend de son alimentation (variable indépendante).
4. La fréquence cardiaque d’une personne (variable dépendante) est affectée par la hauteur à laquelle elle se trouve (variable indépendante).
5. La température ambiante (variable indépendante) influence le nombre d’incendies de forêt (variable dépendante).
6. Le niveau de satisfaction client (variable dépendante) évolue en fonction de la qualité du service rendu (variable indépendante).
7. La publicité d’un produit (variable indépendante) a un impact sur le nombre de ventes dudit produit (variable dépendante).
8. La quantité de substances polluantes émises par un pays (variable dépendante) dépend de la production industrielle de ce pays (variable indépendante).
9. Le salaire d’un chauffeur de taxi (variable dépendante) varie en fonction du nombre de déplacements qu’il effectue (variable indépendante).
10. Le nombre d’habitants d’une ville (variable indépendante) est lié au nombre de taxis dans la ville (variable dépendante).

Gardez à l’esprit qu’une variable est dépendante ou indépendante selon le contexte, car selon l’enquête elle agira comme cause ou comme effet de la relation.

Exercices de variables dépendantes et indépendantes

Dans les cas suivants, quelle est la variable dépendante et quelle est la variable indépendante ?

1. Nombre d’habitants d’une ville – Nombre de bus publics
2. Âge d’un véhicule – État du véhicule
3. Nombre de moustiques – Température ambiante
4. Nombre de jours de pluie par mois – Demande de parapluies

1. Variable dépendante : Nombre de bus publics – Variable indépendante : Nombre d’habitants d’une ville
2. Variable dépendante : Etat du véhicule – Variable indépendante : Âge d’un véhicule
3. Variable dépendante : Nombre de moustiques – Variable indépendante : Température ambiante
4. Variable dépendante : Demande de parapluies – Variable indépendante : Nombre de jours de pluie par mois

Variable dépendante et indépendante en mathématiques

En mathématiques, une relation de cause à effet est généralement modélisée à l’aide d’une variable indépendante et d’une variable dépendante. Ainsi, une fonction définit la relation mathématique qui existe entre la variable dépendante et la variable indépendante.

Les variables dépendantes sont généralement représentées par la lettre y , par contre, la lettre x est généralement utilisée pour indiquer les variables indépendantes.

Par exemple, la fonction y=2x indique que lorsque la variable indépendante x augmente d’une unité, la variable dépendante y augmente deux fois plus.

Pour en savoir plus sur les fonctions mathématiques, vous pouvez consulter notre site Web partenaire, function.xyz .

Variable dépendante et indépendante dans les statistiques

Cependant, en réalité, il est très difficile de trouver une relation entre deux variables pouvant être définie par une fonction mathématique exacte, car parfois la même valeur de la variable indépendante entraîne une valeur différente de la variable dépendante.

Par exemple, parfois, en étudiant davantage, nous obtenons une moins bonne note ou, à l’inverse, en étudiant moins, nous obtenons une meilleure note. Par conséquent, le nombre d’heures que nous consacrons à l’étude n’est pas le seul facteur qui influence la note obtenue, il peut également varier en fonction de la difficulté de l’examen ou de la difficulté de la matière étudiée.

Pour cette raison, en statistique, de nombreuses expériences sont généralement réalisées pour déterminer s’il existe une relation entre deux variables, dont l’une sera la variable indépendante et l’autre la variable dépendante. Ensuite, les résultats obtenus peuvent être représentés graphiquement pour vérifier si les variables sont liées et, si oui, voir quel type de relation elles entretiennent (positive, négative, linéaire, exponentielle…).

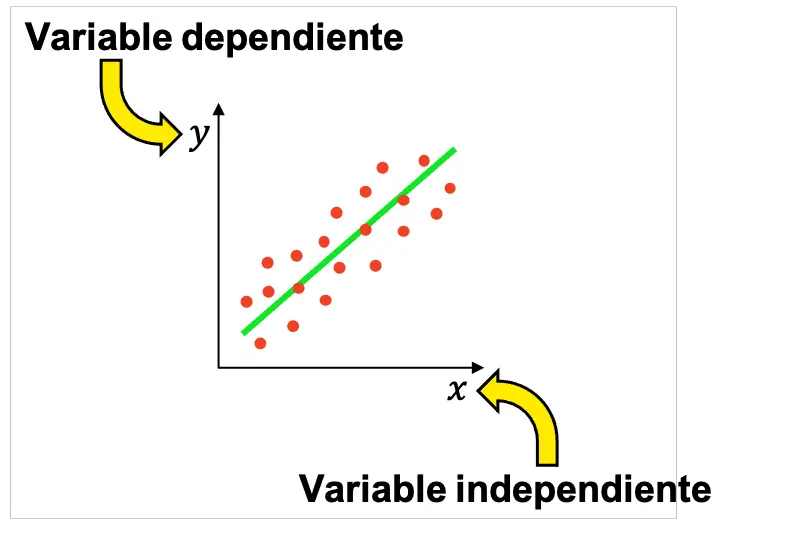
Gardez à l’esprit que dans une enquête, il peut y avoir plus d’une variable indépendante, bien que les études statistiques les plus élémentaires soient réalisées avec une variable indépendante et une variable dépendante.

Une fois l’étude statistique réalisée, une fonction mathématique peut être calculée pour faire une approximation et ainsi modéliser la relation entre les variables. Donc, normalement, un modèle statistique est réalisé en premier, puis un modèle mathématique est réalisé.