Variance
Dans cet article, nous expliquons ce qu’est la variance, également appelée variance, et comment elle est calculée. Vous trouverez la formule de variance, un exemple concret de calcul de variance et, en outre, vous pourrez calculer la variance de n’importe quel ensemble de données avec une calculatrice en ligne.
Nous vous montrons également comment trouver la variance de données groupées, car cela se fait d’une manière différente. Enfin, nous vous apprenons la différence entre la variance de la population et la variance de l’échantillon, la différence entre la variance et l’écart type et les propriétés de cette mesure statistique.
Qu’est-ce que la variance ?
En statistique, la variance est une mesure de dispersion qui indique la variabilité d’une variable aléatoire. La variance est égale à la somme des carrés des résidus divisée par le nombre total d’observations.
Gardez à l’esprit que le résidu s’entend comme la différence entre la valeur d’une donnée statistique et la moyenne de l’ensemble de données.
En théorie des probabilités, le symbole de la variance est la lettre grecque sigma au carré (σ 2 ). Bien qu’il soit également généralement représenté par Var(X) , X étant la variable aléatoire à partir de laquelle la variance est calculée.
En général, l’interprétation de la valeur de variance d’une variable aléatoire est simple. Plus la valeur de la variance est grande, plus les données sont dispersées. Et vice versa, plus la valeur de la variance est petite, moins il y aura de dispersion dans la série de données. Cependant, lors de l’interprétation de la variance, il faut faire attention aux valeurs aberrantes , car elles peuvent fausser la valeur de la variance.
Outre la variance, les autres mesures considérées comme de la dispersion sont l’étendue, l’écart type, l’écart moyen et le coefficient de variation.
Comment calculer l’écart
Pour calculer la variance, les étapes suivantes doivent être effectuées :
- Trouvez la moyenne arithmétique de l’ensemble de données.
- Calculez les résidus, définis comme la différence entre les valeurs et la moyenne de l’ensemble de données.
- Mettez au carré chaque reste.
- Ajoutez tous les résultats calculés à l’étape précédente.
- Divisez par le nombre total de données. Le résultat obtenu est la variance de la série de données.
En conclusion, la formule pour calculer la variance d’un ensemble de données est la suivante :

Où:
 est la variable aléatoire pour laquelle vous souhaitez calculer la variance.
est la variable aléatoire pour laquelle vous souhaitez calculer la variance. est la valeur des données
est la valeur des données .
. est le nombre total d’observations.
est le nombre total d’observations. est la moyenne de la variable aléatoire
est la moyenne de la variable aléatoire .
.
👉 Vous pouvez utiliser la calculatrice ci-dessous pour calculer la variance de n’importe quel ensemble de données.
Par conséquent, pour extraire la variance d’une série de données, il est essentiel que vous sachiez comment la moyenne arithmétique est calculée. Si vous ne vous souvenez pas comment procéder, vous pouvez le consulter dans l’article lié ci-dessus.
Exemple d’écart
Maintenant que nous connaissons la définition de la variance, nous allons résoudre un exercice étape par étape afin que vous puissiez voir comment est obtenue la variance d’une série de données.
- D’une entreprise multinationale, le résultat économique qu’elle a eu au cours des cinq dernières années est connu, dans la plupart elle a obtenu des bénéfices mais une année elle a présenté des pertes considérables : 11,5, 2, -9, 7 millions d’euros. Calculez la variance de cet ensemble de données.
Comme nous l’avons vu dans l’explication ci-dessus, la première chose que nous devons faire pour trouver la variance d’une série de données est de calculer sa moyenne arithmétique :
![]()
Et une fois que nous connaissons la valeur moyenne des données, nous pouvons utiliser la formule de variance :

Nous substituons les données fournies par la déclaration d’exercice dans la formule :
![]()
Finalement, il ne reste plus qu’à résoudre les opérations pour calculer la variance :
![Rendered by QuickLaTeX.com \begin{aligned}Var(X)&=\cfrac{7,8^2+1,8^2+(-1,2)^2+(-12,2)^2+3,8^2}{5}\\[2ex]&=\cfrac{60,84+3,24+1,44+148,84+14,44}{5}\\[2ex]&= \cfrac{228,8}{5} \\[2ex]&=45,76 \ \text{millones de euros}^2\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c2cbee60d77f19e88117e1bcf28d9cb2_l3.png)
Notez que les unités de variance sont les mêmes unités des données statistiques mais élevées au carré, pour cette raison la variance de ce groupe de données est de 45,76 millions d’euros 2 .
Calculateur d’écart
Entrez un ensemble de données statistiques dans la calculatrice suivante pour calculer sa variance. Les données doivent être séparées par un espace et saisies en utilisant le point comme séparateur décimal.
Variance pour les données groupées
Pour calculer la variance des données regroupées en intervalles , les étapes suivantes doivent être suivies :
- Trouvez la moyenne des données groupées.
- Calculez les résidus des données groupées.
- Mettez au carré chaque reste.
- Multipliez chaque résultat précédent par la fréquence de son intervalle.
- Additionnez la somme de toutes les valeurs obtenues à l’étape précédente.
- Divisez par le nombre total d’observations. Le nombre obtenu est la variance des données groupées.
Autrement dit, la formule pour calculer la variance des données regroupées en intervalles est la suivante :
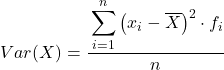
Bien que la formule ci-dessus soit normalement utilisée, l’expression algébrique ci-dessous peut également être utilisée car elle est équivalente :
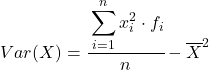
A titre d’exemple, nous allons trouver la variance des séries de données groupées suivantes :
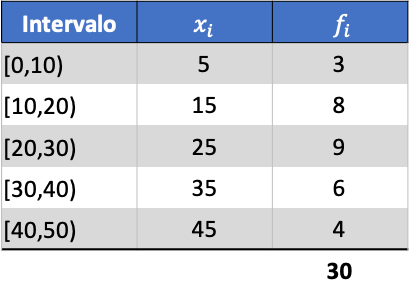
Tout d’abord, nous devons déterminer la moyenne des données groupées. Pour ce faire, on ajoute une colonne dans le tableau des fréquences avec le produit de la note de classe et de la fréquence :
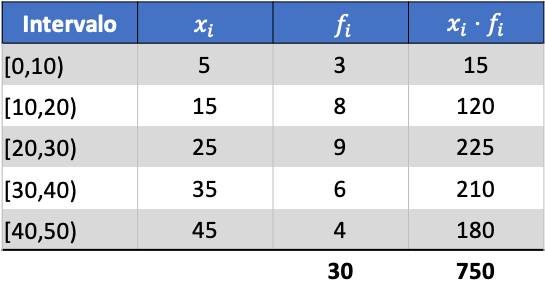
Nous calculons maintenant la moyenne des données regroupées en divisant la somme de la colonne ajoutée par le nombre total de données :
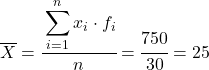
Et à partir de la moyenne des données calculées, nous pouvons ajouter les trois colonnes suivantes :
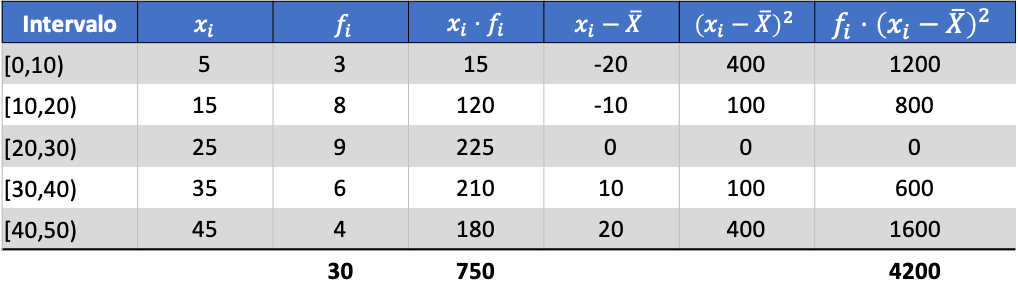
Ainsi, la variance de l’ensemble de données regroupées est la somme de la dernière colonne divisée par le nombre total de données observées :
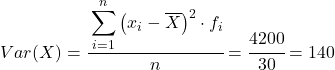
Variance et écart type
La variance et l’écart type (ou écart type) sont deux mesures de dispersion et indiquent donc toutes deux le degré de dispersion de l’ensemble de données. Cependant, la différence entre la variance et l’écart type est qu’en général la variance a des valeurs plus grandes, puisqu’il s’agit du carré de l’écart type.
L’écart type est généralement représenté par la lettre grecque sigma (σ), et pour cette raison la variance est représentée par la lettre sigma élevée au carré (σ 2 ), puisqu’il s’agit de la relation mathématique qui existe entre ces deux métriques de dispersion.
![]()
Ainsi, une fois que vous avez calculé la valeur de la variance d’un ensemble de données, vous pouvez facilement trouver la valeur de l’écart type de ce même ensemble en prenant simplement la racine carrée de la variance.
![]()
Variance de la population et variance de l’échantillon
Logiquement, la variance de la population fait référence au calcul de la variance d’une population statistique et, à la place, la variance de l’échantillon est appliquée au calcul de la variance d’un échantillon. Cependant, il s’agit de deux concepts différents puisque la formule de variance de la population est différente de la formule de variance de l’échantillon.
Normalement, dans les exercices de variance, s’ils ne nous disent pas le contraire, pour trouver la variance de l’ensemble de données fourni, nous devons utiliser la formule de variance de la population , qui est celle que nous avons expliquée au début de l’article :
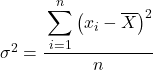
Mais peut-être que dans certains problèmes, on vous demande de traiter les données statistiques comme un échantillon, auquel cas nous devons utiliser la formule de variance de l’échantillon :
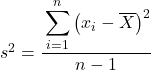
Notez que pour indiquer que la variance d’une population est en cours de calcul, elle est indiquée par la lettre grecque σ, mais lorsque la variance d’un échantillon est calculée, la lettre s est utilisée.
Comme vous pouvez le voir, la seule différence entre les deux formules est que dans la variance d’un échantillon, nous devons diviser par le nombre total d’observations moins 1, par exemple, s’il y a 30 éléments de données au total, nous diviserons par 29. Mais le calcul du numérateur se fait exactement de la même manière.
Propriétés de variance
La variance a les propriétés suivantes :
- La variance de toute variable aléatoire sera toujours supérieure ou égale à zéro. De même, si la variance est égale à zéro, cela signifie que toutes les données statistiques sont identiques.
![]()
- Évidemment, la variance d’une seule valeur est nulle.
![]()
- La variance du produit d’un scalaire par une variable est équivalente à ce scalaire au carré multiplié par la variance de la variable.
![]()
- La variance de la somme de deux variables dépendantes est équivalente à la somme de la variance de chaque variable séparément plus deux fois la covariance entre les deux variables.
![]()
- Par conséquent, si les deux variables sont indépendantes, pour déterminer la variance de leur somme il suffit d’additionner leurs variances :
![]()
- L’écart peut également être défini avec l’espérance mathématique à l’aide de la formule suivante :
![]()
