Comment trouver la variance d’un échantillon sur une calculatrice TI-84
La variance de l’échantillon nous indique dans quelle mesure les valeurs sont réparties dans un échantillon donné.
Généralement noté s 2 , il est calculé comme suit :
s 2 = Σ (x je – x ) 2 / (n-1)
où:
- x : moyenne de l’échantillon
- x i : la ième valeur de l’échantillon
- n : la taille de l’échantillon
L’exemple étape par étape suivant montre comment calculer la variance de l’échantillon pour l’échantillon suivant :
Échantillon : 2, 4, 4, 7, 8, 12, 14, 15, 19, 22
Étape 1 : Saisissez les données
Tout d’abord, nous entrerons les valeurs des données.
Appuyez sur Stat , puis appuyez sur EDIT . Saisissez ensuite les valeurs de l’échantillon dans la colonne L1 :
Étape 2 : Trouver la variance de l’échantillon
Ensuite, appuyez sur Stat , puis faites défiler vers la droite et appuyez sur CALC .
Appuyez ensuite sur 1-Var Stats .
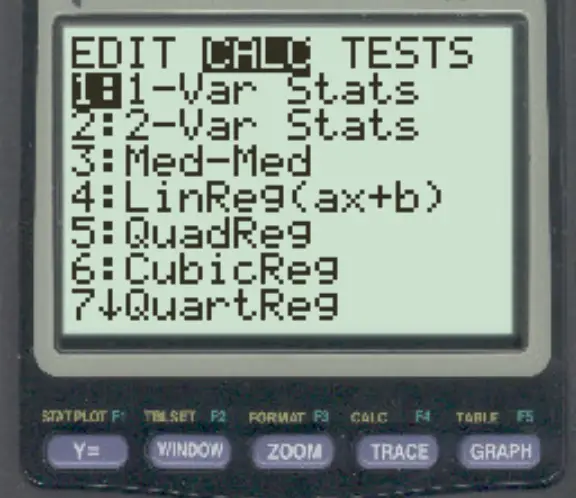
Dans le nouvel écran qui apparaît, appuyez sur Entrée .
Une fois que vous appuyez sur Entrée , une liste de statistiques récapitulatives apparaîtra.
L’écart type de l’échantillon est Sx = 6,783149056 .
Pour trouver la variance de l’échantillon, nous devons mettre cette valeur au carré. Pour cela, appuyez sur VARS puis appuyez sur 5 :
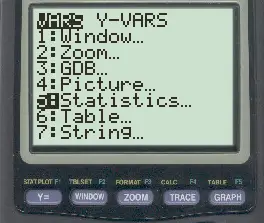
Dans la nouvelle fenêtre qui apparaît, appuyez sur 3 pour sélectionner l’écart type de l’échantillon :
Enfin, appuyez sur le bouton x 2 pour mettre au carré l’écart type de l’échantillon :
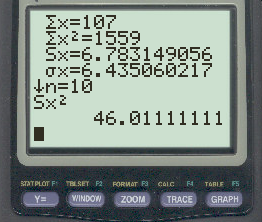
La variance de l’échantillon s’avère être 46,0111 .
Ressources additionnelles
Comment trouver un résumé de cinq chiffres sur une calculatrice TI-84
Comment trouver l’intervalle interquartile sur une calculatrice TI-84
Comment trouver le coefficient de variation sur une calculatrice TI-84
à propos de l'auteur
Dr. Benjamin Anderson
Il est un professeur de statistiques à la retraite devenu éducateur dévoué sur Statorials. Avec une vaste expérience et une expertise dans le domaine des statistiques, je m'engage à partager mes connaissances pour responsabiliser les étudiants grâce à Statorials. Lire plus