Comment trouver la variance des données groupées (avec exemple)

Nous souhaitons souvent calculer la variance d’une distribution de fréquences groupée.

Par exemple, supposons que nous ayons la distribution de fréquence groupée suivante :

Bien qu’il ne soit pas possible de calculer la variance exacte puisque nous ne connaissons pas les valeurs des données brutes , il est possible d’estimer la variance à l’aide de la formule suivante :

Variance : Σn _i (m _i -μ) ² / (N-1)

où:

• n _i : La fréquence du i ^ème groupe
• m _i : Le milieu du i ^ème groupe
• μ : La moyenne
• N : La taille totale de l’échantillon

Remarque : Le point médian de chaque groupe peut être trouvé en prenant la moyenne des valeurs inférieure et supérieure de la plage. Par exemple, le point médian du premier groupe est calculé comme suit : (1+10) / 2 = 5,5.

L’exemple suivant montre comment utiliser cette formule dans la pratique.

Exemple : calculer la variance des données groupées

Supposons que nous ayons les données groupées suivantes :

Voici comment nous utiliserions la formule mentionnée précédemment pour calculer la variance de ces données groupées :

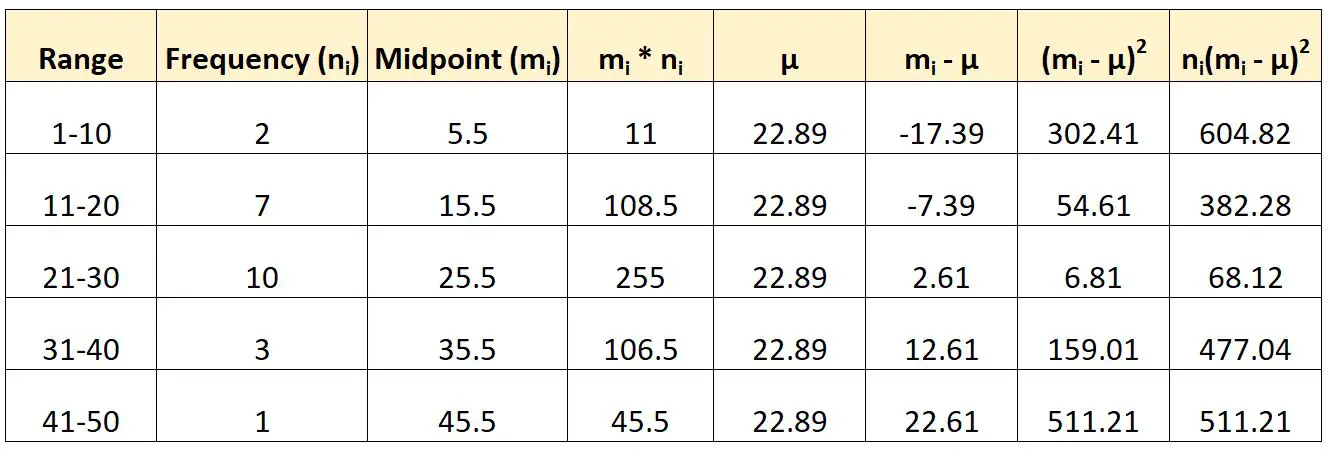
Nous calculerions alors la variance comme suit :

• Variance : Σn _i (m _i -μ) ² / (N-1)
• Écart : (604,82 + 382,28 + 68,12 + 477,04 + 511,21) / (23-1)
• Écart : 92.885

La variance de l’ensemble de données s’avère être de 92,885 .

Ressources additionnelles

Les didacticiels suivants expliquent comment calculer d’autres métriques pour les données groupées :

Comment trouver la moyenne et l’écart type des données groupées
Comment calculer le classement centile pour les données groupées
Comment trouver la médiane des données groupées
Comment trouver le mode des données groupées