Comment effectuer le test t de Welch dans Excel
La manière la plus courante de comparer les moyennes entre deux groupes indépendants consiste à utiliser un test t à deux échantillons . Cependant, ce test suppose que les variances entre les deux groupes sont égales.
Si vous pensez que la variance entre les deux groupes n’est pas égale, vous pouvez utiliser le test t de Welch , qui est l’équivalent non paramétrique du test t à deux échantillons.
Ce didacticiel explique comment effectuer le test t de Welch dans Excel.
Exemple : le test t de Welch dans Excel
Pour cet exemple, nous comparerons les résultats de 12 étudiants qui ont utilisé un livret de préparation à l’examen pour se préparer à l’examen par rapport à 12 étudiants qui ne l’ont pas fait.
Suivez les étapes suivantes pour effectuer un test T de Welch’t afin de déterminer s’il existe une différence dans les résultats moyens à l’examen entre les deux groupes.
Étape 1 : Saisissez les données.
Tout d’abord, saisissez les résultats de l’examen dans deux colonnes :
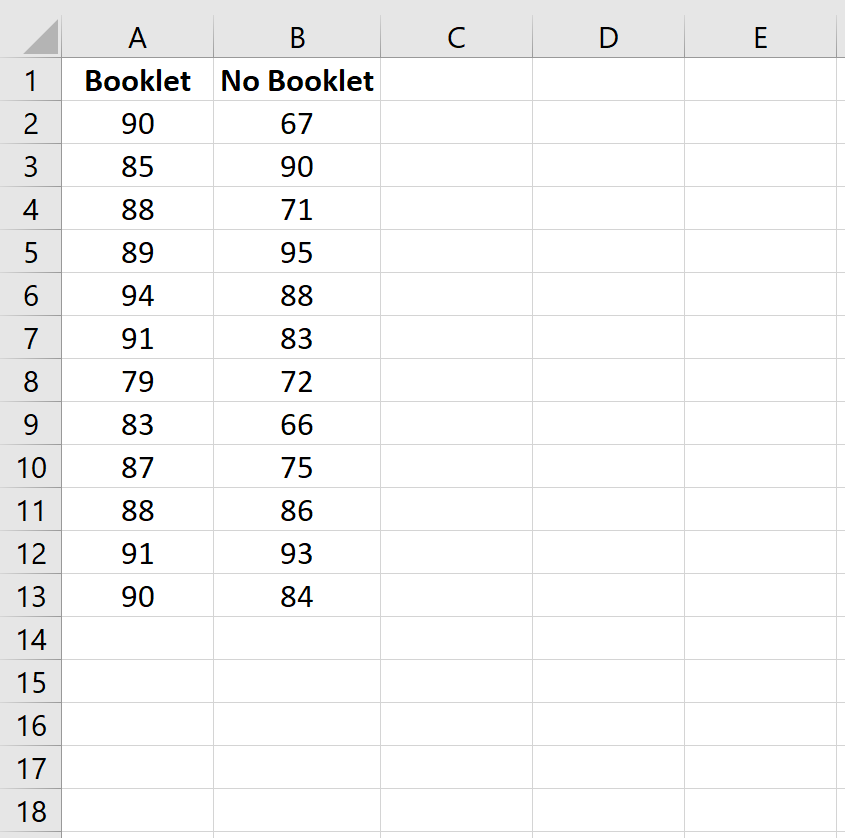
Étape 2 : Effectuez le test t de Welch.
Dans le ruban supérieur d’Excel, accédez à l’onglet Données et cliquez sur Analyse des données . Si vous ne voyez pas cette option, vous devez d’abord installer le logiciel gratuit Analysis ToolPak .

Une fois que vous avez cliqué sur Analyse des données, une nouvelle fenêtre apparaîtra. Sélectionnez Test t : deux échantillons en supposant des variances inégales et cliquez sur OK .
Dans la nouvelle fenêtre, saisissez la plage de valeurs de données pour la Variable 1 et la Variable 2 , y compris leurs étiquettes de groupe. Pour Différence moyenne hypothétique , tapez 0. Cochez la case en regard de Étiquettes . Laissez Alpha réglé sur 0,05. Pour Output Range , choisissez une cellule dans laquelle vous souhaitez que les résultats du test apparaissent. Cliquez ensuite sur OK .
La sortie suivante apparaît automatiquement :
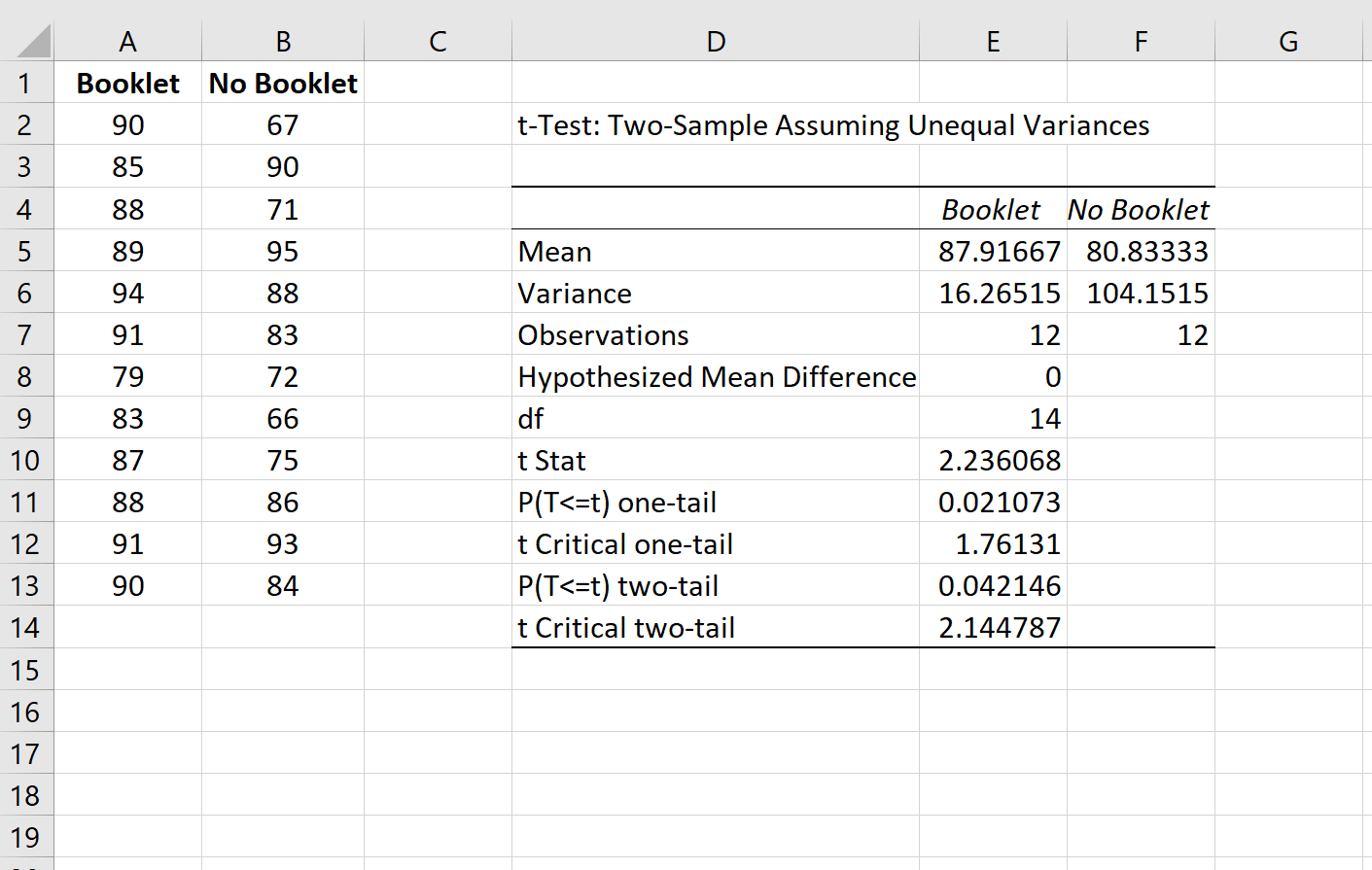
Voici comment interpréter le résultat :
- Moyenne : la note moyenne à l’examen pour chaque groupe.
- Variance : la variance des résultats aux examens pour chaque groupe.
- Observations : la taille de l’échantillon pour chaque groupe.
- Différence moyenne hypothétique : différence moyenne à utiliser dans l’hypothèse nulle du test.
- df : Les degrés de liberté à utiliser avec la statistique de test, calculés comme n 1 + n 2 – 2.
- t Stat : La statistique de test pour le test.
- P(T<=t) unilatéral : la valeur p associée à la statistique de test pour un test unilatéral. Ignorez cela puisque nous effectuons un test bilatéral.
- P(T<=t) bilatéral : valeur p associée à la statistique de test pour un test bilatéral. Puisque celui-ci est inférieur à 0,05, nous rejetterions l’hypothèse nulle et conclurions que la note moyenne à l’examen entre les deux groupes est statistiquement significativement différente au niveau α = 0,05.
Étape 3 : Rapportez les résultats.
Enfin, nous souhaitons rapporter les résultats de notre test t de Welch. Voici un exemple de la façon de procéder :
Un test t de Welch a été effectué pour déterminer s’il y avait une différence statistiquement significative dans les résultats des examens entre un groupe d’étudiants qui utilisaient un livret de préparation à l’examen pour se préparer à l’examen et un groupe qui ne l’utilisait pas. La taille de l’échantillon pour les deux groupes était de 12 étudiants.
Le test t de Welch a révélé qu’il y avait une différence statistiquement significative dans les résultats moyens aux examens (t = 2,236, p = 0,0421) entre les deux groupes.
