Comment effectuer un test de classement signé Wilcoxon dans SAS

Le test de Wilcoxon Signed-Rank est la version non paramétrique du test t pour échantillons appariés .

Il est utilisé pour tester s’il existe ou non une différence significative entre les moyennes de deux populations lorsque la distribution des différences entre les deux échantillons ne peut pas être considérée comme normale.

L’exemple suivant montre comment effectuer un test Wilcoxon Signed-Rank dans SAS.

Exemple : test de classement signé de Wilcoxon dans SAS

Supposons qu’un ingénieur veuille savoir si un nouveau traitement du carburant entraîne une modification du kilométrage moyen par gallon d’une certaine voiture. Pour tester cela, il mesure le mpg de 12 voitures avec et sans traitement du carburant.

Les résultats sont présentés dans le tableau ci-dessous :

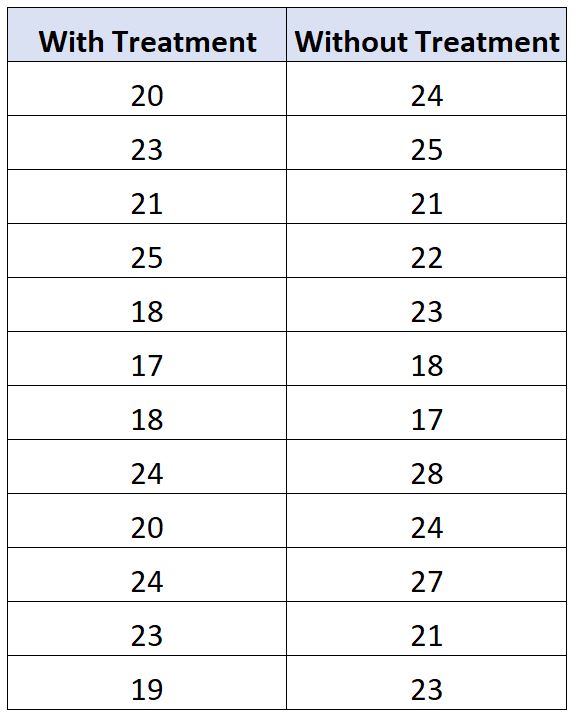
Nous pouvons utiliser le code suivant pour effectuer un test Wilcoxon Signed-Rank dans SAS afin de déterminer s’il existe une différence significative dans le mpg moyen entre les deux groupes :

/*create dataset*/
data my_data;
    input car with_fuel without_fuel;
    datalines;
1 20 24
2 23 25
3 21 21
4 25 22
5 18 23
6 17 18
7 18 17
8 24 28
9 20 24
10 24 27
11 23 21
12 19 23
;
run;

/*create new dataset with difference between two fuel treatments*/
data my_data2;
    set my_data;
    diff=with_fuel-without_fuel;
run;

/*perform Wilcoxon Signed Rank Test*/
proc univariate data=my_data2;
    var diff;
run;

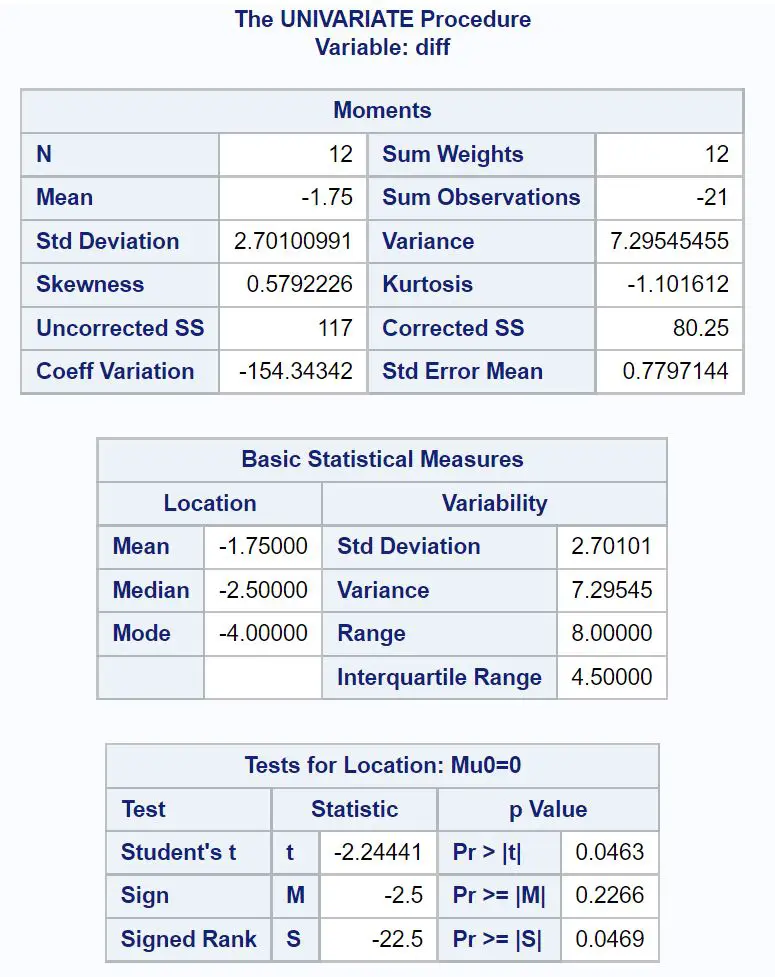
D’après les résultats, nous pouvons voir que la différence moyenne en mpg entre les voitures qui ont reçu le traitement et celles qui ne l’ont pas reçu est de -1,75 .

Dans le tableau intitulé Tests de localisation, nous pouvons observer ce qui suit :

• Statistique du test de classement signé de Wilcoxon : -22,5
• La valeur p correspondante : 0,0469

Rappelons que le test de Wilcoxon Signed-Rank utilise les hypothèses nulles et alternatives suivantes :

• H ₀ : Le mpg est égal entre les deux groupes
• H _A : Le mpg n’est pas égal entre les deux groupes

Puisque la valeur p du test (0,0469) est inférieure à 0,05, nous rejetons l’hypothèse nulle.

Cela signifie que nous avons suffisamment de preuves pour affirmer que le mpg moyen n’est pas égal entre les deux groupes.