Comment effectuer le test de rang signé de Wilcoxon dans R

Le test de Wilcoxon Signed-Rank est la version non paramétrique du test t apparié . Il est utilisé pour tester s’il existe ou non une différence significative entre les moyennes de deux populations lorsque la distribution des différences entre les deux échantillons ne peut pas être considérée comme normale.

Ce didacticiel explique comment effectuer un test de rang signé de Wilcoxon dans R.

Exemple : test de rang signé de Wilcoxon dans R

Supposons qu’un entraîneur de basket-ball veuille savoir si un certain programme d’entraînement augmente le nombre de lancers francs effectués par ses joueurs. Pour tester cela, il demande à 15 joueurs de réaliser 20 lancers francs chacun avant et après le programme d’entraînement.

Puisque chaque joueur peut être « jumelé » avec lui-même, l’entraîneur avait prévu d’utiliser un test t jumelé pour déterminer s’il y avait une différence significative entre le nombre moyen de lancers francs effectués avant et après le programme d’entraînement. Cependant, la répartition des différences s’avère non normale, c’est pourquoi l’entraîneur utilise plutôt un test de Wilcoxon Signed-Rank.

Le tableau suivant présente le nombre de lancers francs réalisés (sur 20 tentatives) par chacun des 15 joueurs, avant et après le programme d’entraînement :

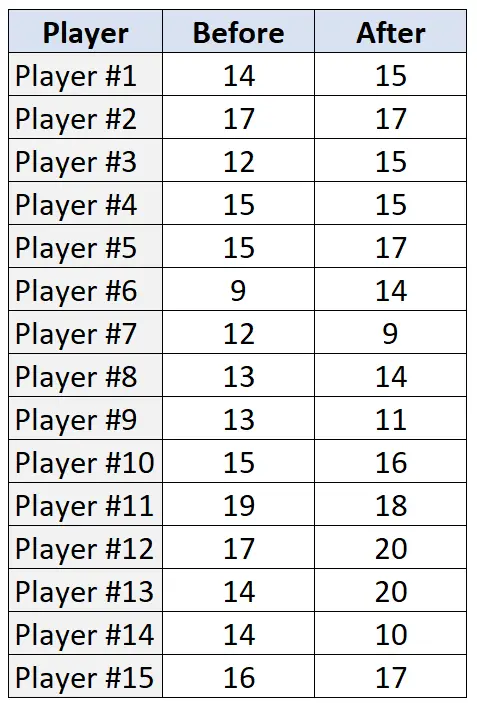
Pour effectuer le Wilcoxon Signed-Rank Test sur ces données dans R, nous pouvons utiliser la fonction wilcox.test() , qui utilise la syntaxe suivante :

wilcox.test (x, y, paire = VRAI)

où:

• x, y : deux vecteurs de valeurs de données
• paired : définir ceci sur TRUE indique à R que nos deux vecteurs contenaient des données appariées

Le code suivant illustre comment utiliser cette fonction pour effectuer le test de Wilcoxon Signed-Rank sur ces données :

#create the two vectors of data
before <- c(14, 17, 12, 15, 15, 9, 12, 13, 13, 15, 19, 17, 14, 14, 16)
after <- c(15, 17, 15, 15, 17, 14, 9, 14, 11, 16, 18, 20, 20, 10, 17)

#perform Wilcoxon Signed-Rank Test
wilcox.test(before, after, paired=TRUE)

	Wilcoxon signed rank test with continuity correction

data:  before and after
V = 29.5, p-value = 0.275
alternative hypothesis: true location shift is not equal to 0

La statistique du test est de 29,5 et la valeur p correspondante est de 0,275 . Puisque cette valeur p n’est pas inférieure à 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle. Il n’y a pas de différence statistiquement significative dans le nombre de lancers francs avant et après la participation des joueurs au programme d’entraînement.

Par défaut, cette fonction effectue un test de Wilcoxon Signed-Rank bilatéral, mais vous pouvez spécifier un test de gauche ou un test de droite en utilisant l’argument alternatif :

#perform left-tailed Wilcoxon Signed-Rank Test
wilcox.test(before, after, paired=TRUE, alternative="less")

	Wilcoxon signed rank test with continuity correction

data:  before and after
V = 29.5, p-value = 0.1375
alternative hypothesis: true location shift is less than 0

#perform right-tailed Wilcoxon Signed-Rank Test
wilcox.test(before, after, paired=TRUE, alternative="greater")

	Wilcoxon signed rank test with continuity correction

data:  before and after
V = 29.5, p-value = 0.8774
alternative hypothesis: true location shift is greater than 0

Ressources additionnelles

Une introduction au test de classement signé de Wilcoxon
Calculateur de test de classement signé Wilcoxon