Correction de continuité de Yate : définition & Exemple

Un test d’indépendance du chi carré est utilisé pour déterminer s’il existe ou non une association significative entre deux variables catégorielles.

Ce test utilise les hypothèses nulles et alternatives suivantes :

• H ₀ : (hypothèse nulle) Les deux variables sont indépendantes.
• H ₁ : (hypothèse alternative) Les deux variables ne sont pas indépendantes. (c’est-à-dire qu’ils sont associés)

Nous utilisons la formule suivante pour calculer la statistique du test du Chi carré X ² pour ce test :

X ² = Σ(O _je -E _je ) ² / E _je

où:

• Σ : est un symbole fantaisiste qui signifie « somme »
• O : valeur observée
• E : valeur attendue

Ce test suppose que les probabilités discrètes des fréquences dans un tableau de contingence peuvent être approximées par la distribution du Chi carré, qui est une distribution continue.

Cependant, cette hypothèse tend à être légèrement incorrecte et les statistiques de test qui en résultent tendent à être biaisées à la hausse.

Pour corriger ce biais, nous pouvons appliquer la correction de continuité de Yate , qui applique la correction suivante à la formule X ² :

X ² = Σ(|O _je -E _je | – 0,5) ² / E _je

Nous n’utilisons généralement cette correction que lorsqu’au moins une cellule du tableau de contingence a une fréquence attendue inférieure à 5.

Exemple : application de la correction de continuité de Yate

Supposons que nous voulions savoir si le genre est associé ou non à la préférence pour un parti politique. Nous prenons un échantillon aléatoire simple de 40 électeurs et les interrogeons sur leur préférence en matière de parti politique. Le tableau suivant présente les résultats de l’enquête :

Voici comment effectuer un test d’indépendance du chi carré avec la correction de continuité de Yate :

Valeurs observées :

Valeurs attendues :

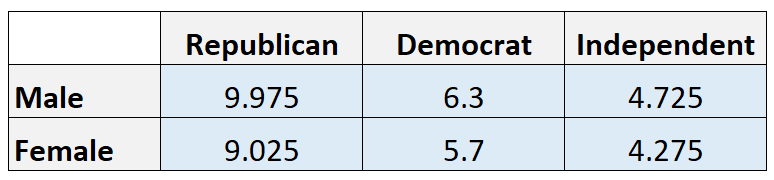
Remarque : Nous calculons la valeur attendue dans chaque cellule en multipliant le total de la ligne par le total de la colonne, puis en divisant par le total général. Par exemple, le nombre attendu d’hommes républicains est de (21*19)/40 = 9,975.

Statistique du test du chi carré : X ² = Σ(|O _i -E _i | – 0,5) ² / E _i

• (|8-9,975| – 0,5) ² / 9,975 = 0,218
• (|9-6,3| – 0,5) ² / 6,3 = 0,768
• (|4-4,725| – 0,5) ² / 4,725 = 0,011
• (|11-9,025| – 0,5) ² / 9,025 = 0,241
• (|3-5,7| – 0,5) ² / 5,7 = 0,849
• (|5-4,275| – 0,5) ² / 4,275 = 0,012

Ainsi, X ² = 0,218 + 0,768 + 0,011 + 0,241 + 0,849 + 0,012 = 2,099

Valeur P : selon le calculateur du chi carré à la valeur P , la valeur p qui correspond à une statistique de test du chi carré avec 2 degrés de liberté est de 0,3501 .

Puisque cette valeur p n’est pas inférieure à 0,05, nous ne parviendrons pas à rejeter l’hypothèse nulle. Cela signifie que nous ne disposons pas de preuves suffisantes pour affirmer qu’il existe une association entre le sexe et les préférences en matière de parti politique.