Comment calculer les scores Z dans Excel
En statistiques, un score z nous indique à combien d’écarts types une valeur se trouve par rapport à la moyenne . Nous utilisons la formule suivante pour calculer un z-score :
z = (X – μ) / σ
où:
- X est une valeur de données brutes unique
- μ est la moyenne de l’ensemble de données
- σ est l’écart type de l’ensemble de données
Ce didacticiel explique comment calculer les scores z pour les valeurs de données brutes dans Excel.
Comment calculer les scores Z dans Excel
Supposons que nous disposions de l’ensemble de données suivant et que nous souhaitions trouver le score z pour chaque valeur de données brutes :
Nous pouvons effectuer les étapes suivantes pour ce faire.
Étape 1 : Trouvez la moyenne et l’écart type de l’ensemble de données.
Tout d’abord, nous devons trouver la moyenne et l’écart type de l’ensemble de données. Les formules suivantes montrent comment procéder :
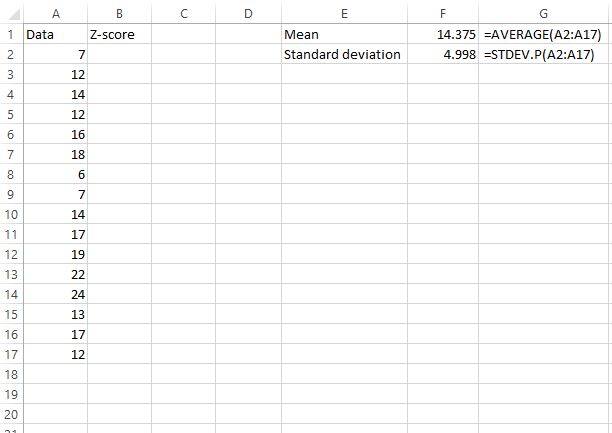
La moyenne s’avère être de 14,375 et l’écart type est de 4,998 .
Étape 2 : Recherchez le score z pour la première valeur de données brutes.
Ensuite, nous trouverons le score z pour la première valeur de données brutes en utilisant la formule z = (X – μ) / σ.
La cellule C2 montre la formule que nous avons utilisée pour calculer la valeur z dans la cellule B2.
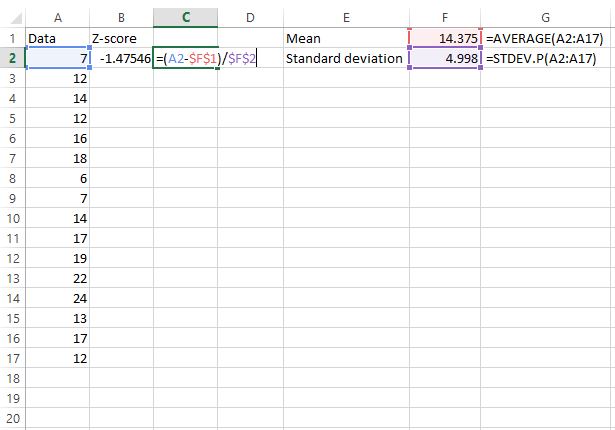
Étape 3 : Recherchez les scores z pour toutes les valeurs restantes.
Maintenant que nous avons trouvé le score z pour la première valeur de l’ensemble de données, nous pouvons simplement copier la formule que nous avons utilisée dans la cellule B2 dans le reste des valeurs de données. Nous pouvons le faire en mettant en surbrillance toute la colonne du score z, en commençant par le premier score z que nous avons déjà calculé :
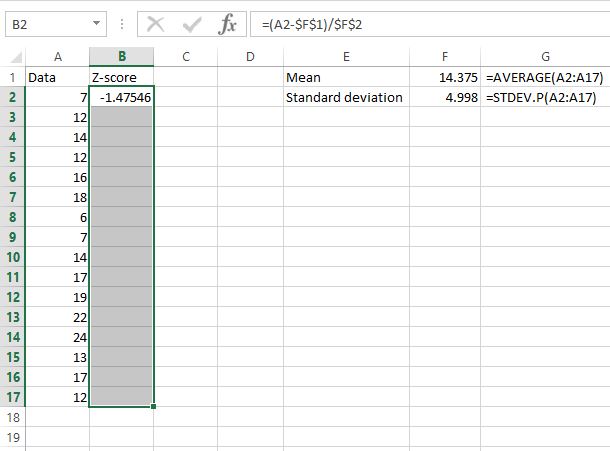
Ensuite, appuyez sur Ctrl+D . Cela copie la formule de la première cellule dans toutes les cellules situées en dessous.
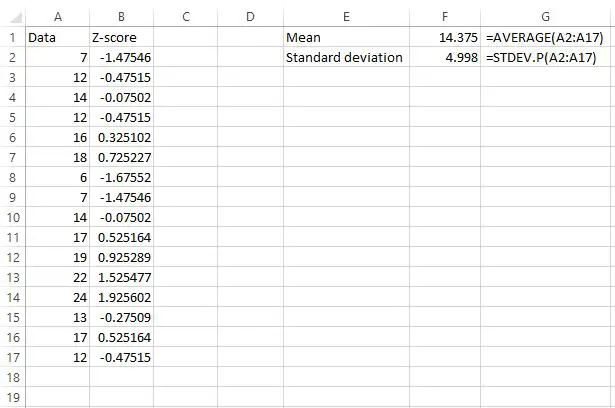
Nous avons maintenant trouvé le score z pour chaque valeur de données brutes.
Comment interpréter les scores Z dans Excel
Rappelez-vous qu’un score z nous indique simplement à combien d’écarts types une valeur se trouve par rapport à la moyenne.
Un score z peut être positif, négatif ou égal à zéro.
Un score z positif indique qu’une valeur particulière est supérieure à la moyenne, un score z négatif indique qu’une valeur particulière est inférieure à la moyenne et un score z de zéro indique qu’une valeur particulière est égale à la moyenne.
Dans notre exemple, nous avons constaté que la moyenne était de 14,375 et l’écart type de 4,998 .
Ainsi, la première valeur de notre ensemble de données était 7, qui avait un score z de (7-14,375) / 4,998 = -1,47546 . Cela signifie que la valeur « 7 » est inférieure de -1,47545 écarts types à la moyenne.
La valeur suivante dans nos données, 12, avait un score z de (12-14,375) / 4,998 = -0,47515 . Cela signifie que la valeur « 12 » est inférieure de -0,47515 écart-type à la moyenne.

Plus une valeur est éloignée de la moyenne, plus la valeur absolue du score z sera élevée pour cette valeur.
Par exemple, la valeur 7 est plus éloignée de la moyenne (14,375) que la valeur 12, ce qui explique pourquoi 7 avait un z-score avec une valeur absolue plus grande.
Ressources additionnelles
Les articles suivants fournissent des informations supplémentaires sur la façon de travailler avec les scores z dans Excel :
Comment trouver une valeur P à partir d’un score Z dans Excel
Comment convertir entre les scores Z et les centiles dans Excel
