Normalisation du score Z : définition & Exemples

La normalisation du score Z fait référence au processus de normalisation de chaque valeur d’un ensemble de données de telle sorte que la moyenne de toutes les valeurs soit de 0 et l’écart type soit de 1.

Nous utilisons la formule suivante pour effectuer une normalisation du score z sur chaque valeur d’un ensemble de données :

Nouvelle valeur = (x – μ) / σ

où:

• x : Valeur d’origine
• μ : Moyenne des données
• σ : Écart type des données

L’exemple suivant montre comment effectuer une normalisation du score z sur un ensemble de données dans la pratique.

Exemple : exécution de la normalisation du score Z

Supposons que nous ayons l’ensemble de données suivant :

À l’aide d’une calculatrice, nous pouvons constater que la moyenne de l’ensemble de données est de 21,2 et l’écart type est de 29,8 .

Pour effectuer une normalisation du z-score sur la première valeur de l’ensemble de données, nous pouvons utiliser la formule suivante :

• Nouvelle valeur = (x – μ) / σ
• Nouvelle valeur = (3 – 21,2) / 29,8
• Nouvelle valeur = -0,61

Nous pouvons utiliser cette formule pour effectuer une normalisation du score z sur chaque valeur de l’ensemble de données :

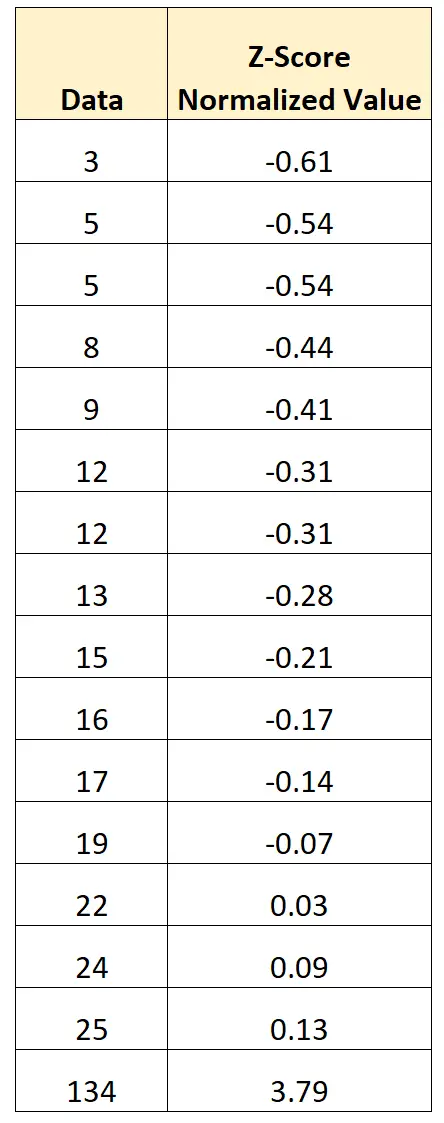
La moyenne des valeurs normalisées est 0 et l’écart type des valeurs normalisées est 1 .

Les valeurs normalisées représentent le nombre d’écarts types entre la valeur d’origine et la moyenne.

Par exemple:

• La première valeur de l’ensemble de données est de 0,61 écart-type en dessous de la moyenne.
• La deuxième valeur de l’ensemble de données est de 0,54 écart-type en dessous de la moyenne.
• …
• La dernière valeur de l’ensemble de données est de 3,79 écarts types au-dessus de la moyenne.

L’avantage d’effectuer ce type de normalisation est que la valeur aberrante évidente dans l’ensemble de données (134) a été transformée de telle manière qu’elle n’est plus une valeur aberrante massive.

Si nous utilisons ensuite cet ensemble de données pour ajuster un certain type de modèle d’apprentissage automatique , la valeur aberrante n’aura plus autant d’influence qu’elle pourrait avoir sur l’ajustement du modèle.

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur différentes techniques de normalisation :

Standardisation ou normalisation : quelle est la différence ?
Comment normaliser les données entre 0 et 1
Comment normaliser les données entre 0 et 100