Comment calculer les scores Z dans SAS

En statistiques, un score z nous indique à combien d’écarts types une valeur se trouve par rapport à la moyenne .

Nous utilisons la formule suivante pour calculer un z-score :

z = (X – μ) / σ

où:

• X est une valeur de données brutes unique
• μ est la moyenne de l’ensemble de données
• σ est l’écart type de l’ensemble de données

L’exemple suivant montre comment calculer les scores z pour les valeurs de données brutes dans SAS.

Exemple : calculer les scores Z dans SAS

Supposons que nous créions l’ensemble de données suivant dans SAS :

/*create dataset*/
data original_data;
    input values;
    datalines;
7
12
14
12
16
18
6
7
14
17
19
22
24
13
17
12
;
run;

/*view dataset*/
proc print data=original_data;

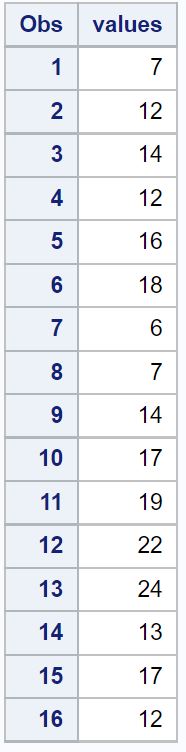
Supposons maintenant que nous souhaitions calculer le score z pour chaque valeur de l’ensemble de données.

Nous pouvons utiliser proc sql pour ce faire :

/*create new variable that shows z-scores for each raw data value*/
proc sql;
    select values, (values - mean(values)) / std(values) as z_scores
    from original_data;
quit;

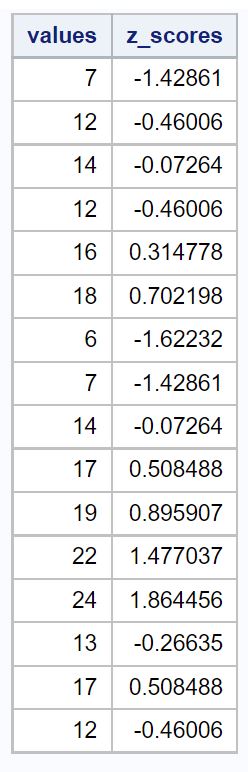
La colonne valeurs affiche les valeurs des données d’origine et la colonne z_scores affiche le score z pour chaque valeur.

Comment interpréter les scores Z dans SAS

Un score z nous indique à combien d’écarts types une valeur se trouve par rapport à la moyenne.

Un score z peut être positif, négatif ou égal à zéro.

Un score z positif indique qu’une valeur particulière est supérieure à la moyenne, un score z négatif indique qu’une valeur particulière est inférieure à la moyenne et un score z de zéro indique qu’une valeur particulière est égale à la moyenne.

Si nous calculions la moyenne et l’écart type de notre ensemble de données, nous constaterions que la moyenne est de 14,375 et l’écart type est de 5,162 .

Ainsi, la première valeur de notre ensemble de données était 7, qui avait un score z de (7-14,375) / 5,162 = -1,428 . Cela signifie que la valeur « 7 » est inférieure de 1,428 écart-type à la moyenne.

La valeur suivante dans nos données, 12, avait un score z de (12-14,375) / 5,162 = -0,46 . Cela signifie que la valeur « 12 » est inférieure de 0,46 écart-type à la moyenne.

Plus une valeur est éloignée de la moyenne, plus la valeur absolue du score z sera élevée pour cette valeur.

Par exemple, la valeur 7 est plus éloignée de la moyenne (14,375) que la valeur 12, ce qui explique pourquoi 7 avait un z-score avec une valeur absolue plus grande.

Ressources additionnelles

Les articles suivants expliquent comment effectuer d’autres tâches courantes dans SAS :

Comment identifier les valeurs aberrantes dans SAS
Comment calculer les centiles dans SAS
Comment calculer la moyenne, la médiane et le mode dans SAS