Comment effectuer une régression cubique en Python

La régression cubique est un type de régression que nous pouvons utiliser pour quantifier la relation entre une variable prédictive et une variable de réponse lorsque la relation entre les variables est non linéaire.

Ce tutoriel explique comment effectuer une régression cubique en Python.

Exemple : régression cubique en Python

Supposons que nous ayons le DataFrame pandas suivant qui contient deux variables (x et y) :

import pandas as pd

#create DataFrame
df = pd.DataFrame({'x': [6, 9, 12, 16, 22, 28, 33, 40, 47, 51, 55, 60],
                   'y': [14, 28, 50, 64, 67, 57, 55, 57, 68, 74, 88, 110]})

#view DataFrame
print(df)

     x    y
0    6   14
1    9   28
2   12   50
3   16   64
4   22   67
5   28   57
6   33   55
7   40   57
8   47   68
9   51   74
10  55   88
11  60  110

Si nous faisons un simple nuage de points de ces données, nous pouvons voir que la relation entre les deux variables est non linéaire :

import matplotlib.pyplot as plt

#create scatterplot
plt.scatter(df.x, df.y)

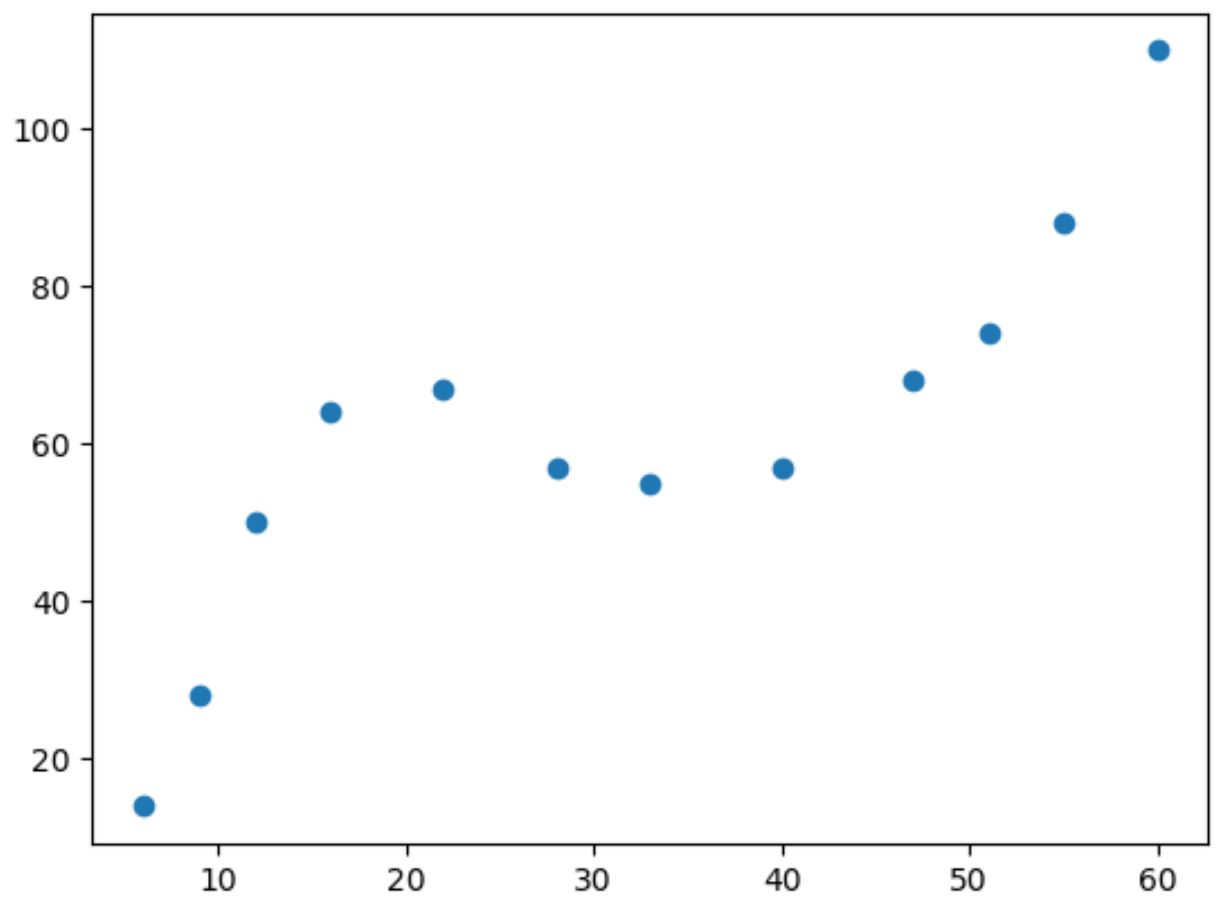
À mesure que la valeur de x augmente, y augmente jusqu’à un certain point, puis diminue, puis augmente à nouveau.

Ce modèle avec deux « courbes » dans le tracé est une indication d’une relation cubique entre les deux variables.

Cela signifie qu’un modèle de régression cubique est un bon candidat pour quantifier la relation entre les deux variables.

Pour effectuer une régression cubique, nous pouvons ajuster un modèle de régression polynomiale avec un degré de 3 à l’aide de la fonction numpy.polyfit() :

import numpy as np

#fit cubic regression model
model = np.poly1d(np.polyfit(df.x, df.y, 3))

#add fitted cubic regression line to scatterplot
polyline = np.linspace(1, 60, 50)
plt.scatter(df.x, df.y)
plt.plot(polyline, model(polyline))

#add axis labels
plt.xlabel('x')
plt.ylabel('y')

#display plot
plt.show()

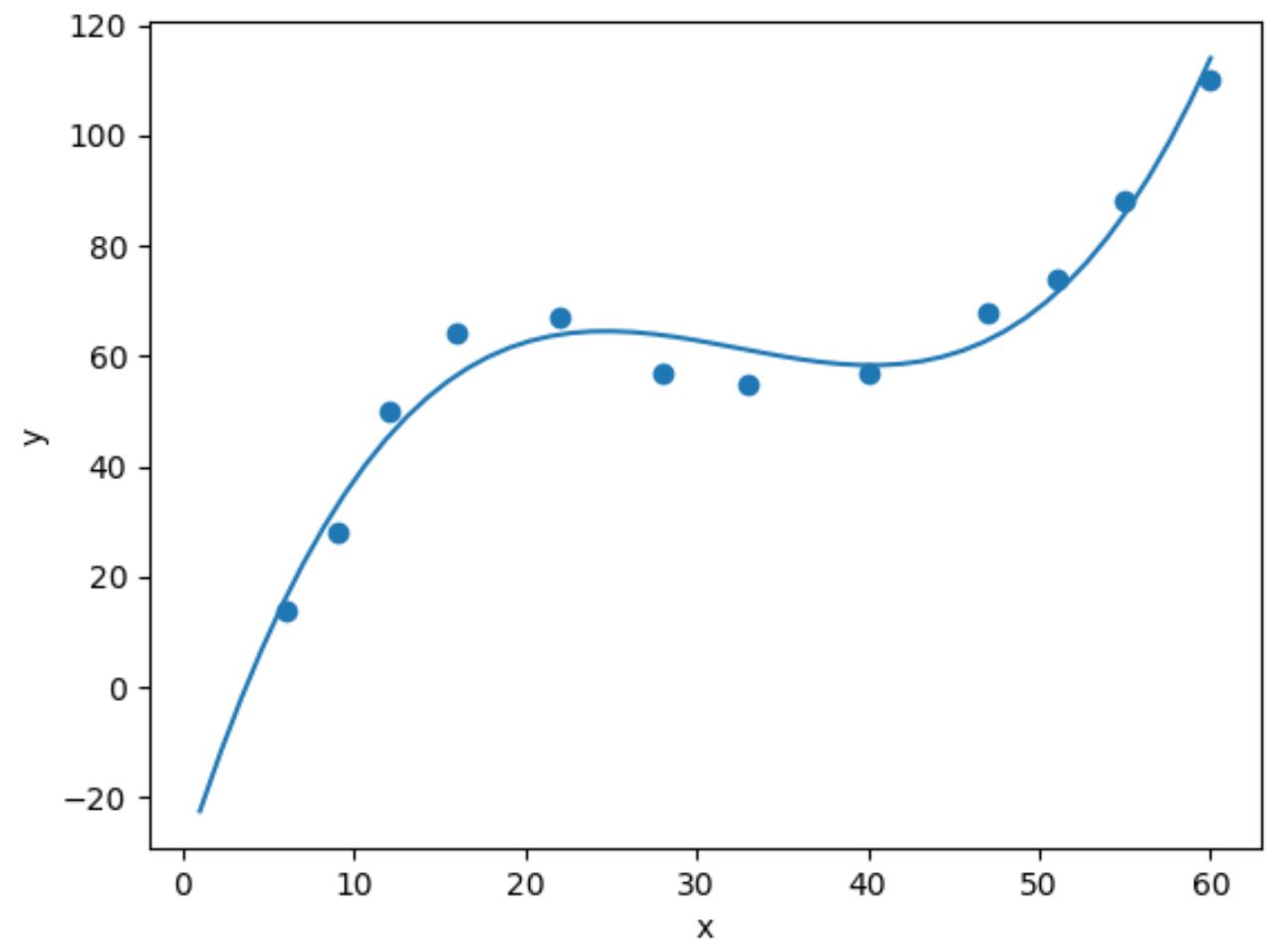
Nous pouvons obtenir l’équation de régression cubique ajustée en imprimant les coefficients du modèle :

print(model)

          3          2
0.003302 x - 0.3214 x + 9.832 x - 32.01

L’équation de régression cubique ajustée est la suivante :

y = 0,003302(x) ³ – 0,3214(x) ² + 9,832x – 30,01

Nous pouvons utiliser cette équation pour calculer la valeur attendue de y en fonction de la valeur de x.

Par exemple, si x est égal à 30, alors la valeur attendue pour y est 64,844 :

y = 0,003302(30) ³ – 0,3214(30) ² + 9,832(30) – 30,01 = 64,844

Nous pouvons également écrire une courte fonction pour obtenir le R au carré du modèle, qui est la proportion de la variance de la variable de réponse qui peut être expliquée par les variables prédictives.

#define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = np.polyfit(x, y, degree)
    p = np.poly1d(coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = np.sum(y)/len(y)
    ssreg = np.sum((yhat-ybar)**2)
    sstot = np.sum((y - ybar)**2)
    results['r_squared'] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(df.x, df.y, 3)

{'r_squared': 0.9632469890057967}

Dans cet exemple, le R carré du modèle est 0,9632 .

Cela signifie que 96,32 % de la variation de la variable de réponse peut être expliquée par la variable prédictive.

Étant donné que cette valeur est si élevée, cela nous indique que le modèle de régression cubique quantifie bien la relation entre les deux variables.

Connexes : Qu’est-ce qu’une bonne valeur R au carré ?

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes en Python :

Comment effectuer une régression linéaire simple en Python
Comment effectuer une régression quadratique en Python
Comment effectuer une régression polynomiale en Python