Comment trouver la probabilité à partir d’un score Z : avec des exemples
Le moyen le plus simple de trouver la probabilité à partir d’un score z consiste simplement à rechercher la probabilité qui correspond au score z dans le tableau z .
Ce didacticiel explique comment utiliser la table z pour trouver les probabilités suivantes :
- La probabilité qu’une valeur soit inférieure à un certain score z.
- La probabilité qu’une valeur soit supérieure à un certain score z.
- La probabilité qu’une valeur soit comprise entre deux certains scores z.
Allons-y !
Exemple 1 : Probabilité inférieure à un certain score Z
Supposons que nous souhaitions trouver la probabilité qu’une valeur dans une distribution donnée ait un score z inférieur à z = 0,25 .
Pour trouver cette probabilité, nous devons rechercher 0,25 dans la table z :
La probabilité qu’une valeur dans une distribution donnée ait un score z inférieur à z = 0,25 est d’environ 0,5987 .
Remarque : Cela pourrait également s’écrire 59,87 % en termes de pourcentage.
Exemple 2 : Probabilité supérieure à un certain score Z
Supposons que nous souhaitions trouver la probabilité qu’une valeur dans une distribution donnée ait un score z supérieur à z = -0,5 .
Pour trouver cette probabilité, nous devons rechercher -0,5 dans la table z :
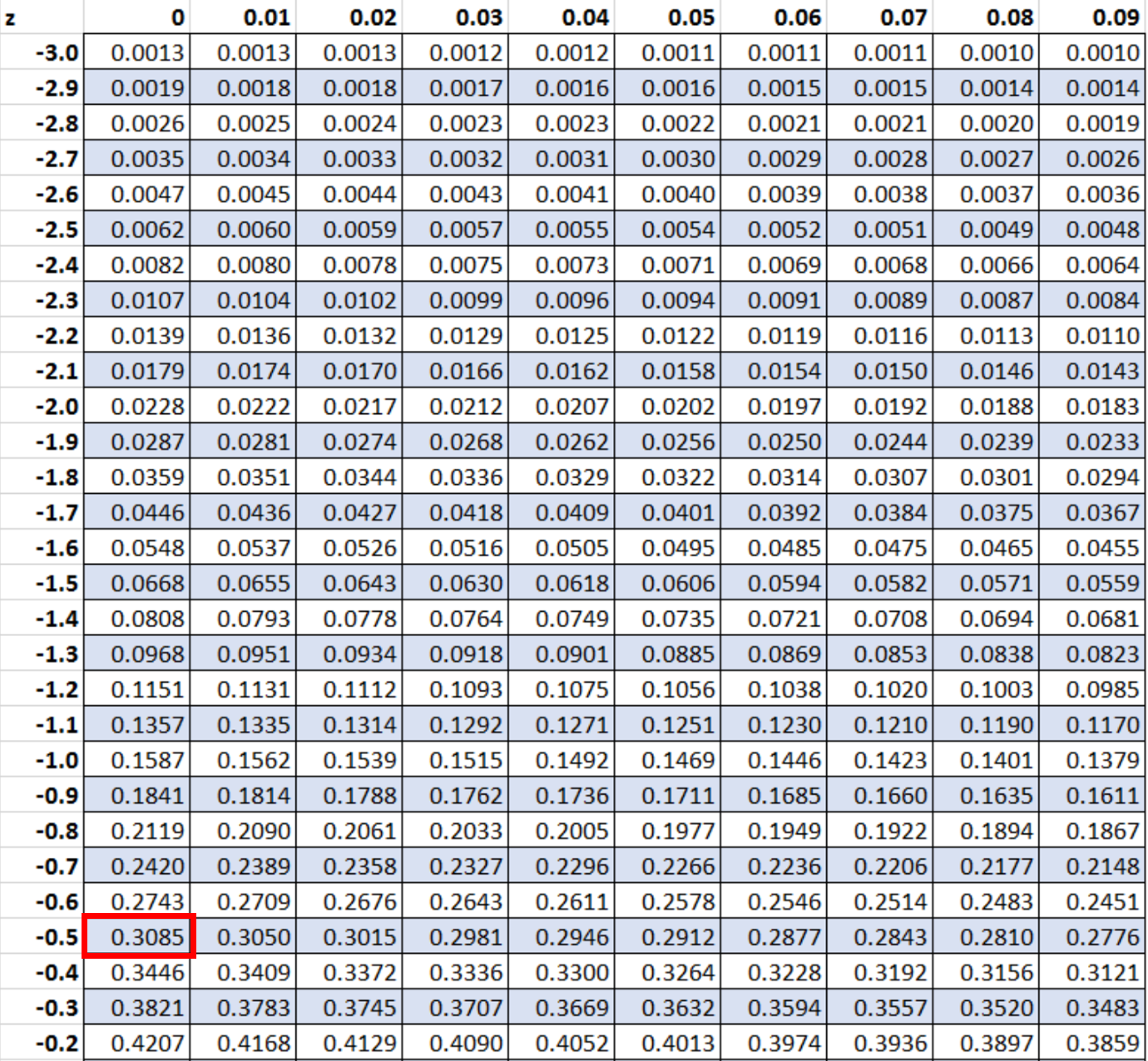
La probabilité qui correspond à un score z de -0,5 est de 0,3085.
Cependant, puisque nous voulons connaître la probabilité qu’une valeur dans une distribution donnée ait un score z supérieur à -0,5, nous devons soustraire cette probabilité de 1.
Ainsi, la probabilité qu’une valeur dans une distribution donnée ait un score z supérieur à -0,5 est : 1 – 0,3085 = 0,6915 .
Exemple 3 : Probabilité entre deux scores Z
Supposons que nous souhaitions trouver la probabilité qu’une valeur dans une distribution donnée ait un score z compris entre z = 0,4 et z = 1 .
Tout d’abord, nous rechercherons la valeur 0,4 dans la table z :
Ensuite, nous rechercherons la valeur 1 dans la table z :
Ensuite, nous soustrairons la plus petite valeur de la plus grande valeur : 0,8413 – 0,6554 = 0,1859 .
Ainsi, la probabilité qu’une valeur dans une distribution donnée ait un score z compris entre z = 0,4 et z = 1 est d’environ 0,1859 .
Ressources additionnelles
Les didacticiels suivants fournissent des informations supplémentaires sur les scores z :
5 exemples d’utilisation des Z-Scores dans la vie réelle
Comment convertir les scores Z en scores bruts
Comment trouver les scores Z dans une zone donnée
à propos de l'auteur
Dr. Benjamin Anderson
Il est un professeur de statistiques à la retraite devenu éducateur dévoué sur Statorials. Avec une vaste expérience et une expertise dans le domaine des statistiques, je m'engage à partager mes connaissances pour responsabiliser les étudiants grâce à Statorials. Lire plus