Comment simuler & Tracer une distribution normale bivariée dans R

En statistique, deux variables suivent une distribution normale bivariée si elles ont une distribution normale lorsqu’elles sont additionnées.

Ce didacticiel explique comment effectuer les tâches suivantes dans R :

• Simuler une distribution normale bivariée
• Tracer une distribution normale bivariée à l’aide d’un tracé de contour (tracé 2D)
• Tracer une distribution normale bivariée à l’aide d’un tracé de surface (tracé 3D)

Allons-y !

Exemple 1 : Simuler une distribution normale bivariée dans R

Le moyen le plus simple de simuler une distribution normale bivariée dans R consiste à utiliser la fonction mvrnorm() du package MASS .

Le code suivant montre comment utiliser cette fonction pour simuler une distribution normale bivariée en pratique :

library(MASS)

#make this example reproducible
set.seed(0)

#simulate bivariate normal distribution
bivariate_data <- as.data.frame(mvrnorm(n=100,
                                        mu=c(0, 0),
                                        Sigma=matrix(c(5, 3, 4, 4), ncol=2)))

#view first six rows of bivariate dataset
head(bivariate_data)

           V1         V2
1 -2.03600343 -2.9623059
2  0.07719131  1.2948982
3 -3.26729701 -1.7928069
4 -2.62985132 -2.3015471
5 -1.75126215  0.3056698
6  3.67698436  2.2020238

Voici ce que fait chaque argument de la fonction mvrnorm() :

• n : Définit la taille de l’échantillon
• mu : Définit la moyenne de chaque variable
• Sigma : Définit la matrice de covariance des deux variables

Le résultat final est un bloc de données avec deux variables qui suivent une distribution normale une fois additionnées.

Exemple 2 : tracer une distribution normale bivariée

Le moyen le plus simple de tracer une distribution normale bivariée dans R consiste à utiliser les fonctions du package mnormt() .

Par exemple, nous pouvons utiliser la fonction contour() de ce package pour créer un tracé de contour, qui offre une visualisation 2D de la distribution normale bivariée :

library(mnormt)

#make this example reproducible
set.seed(0)

#create bivariate normal distribution
x     <- seq(-3, 3, 0.1) 
y     <- seq(-3, 3, 0.1)
mu    <- c(0, 0)
sigma <- matrix(c(2, -1, -1, 2), nrow=2)
f     <- function(x, y) dmnorm(cbind(x, y), mu, sigma)
z     <- outer(x, y, f)

#create contour plot
contour(x, y, z)

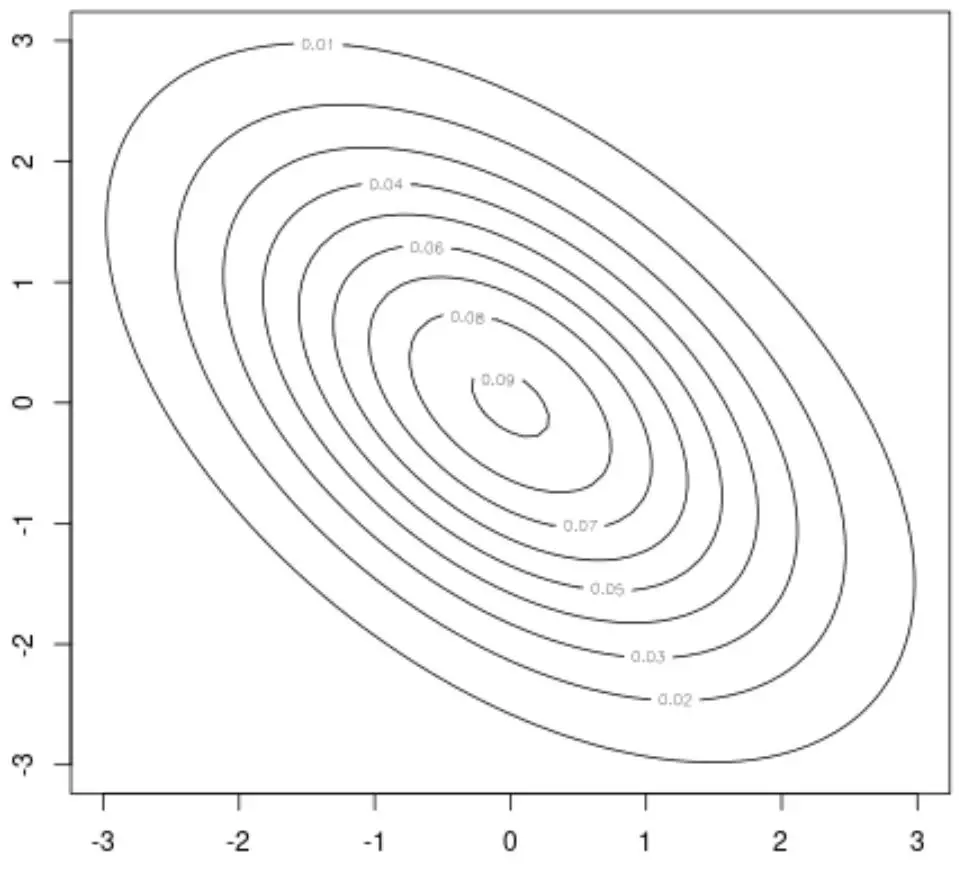
Nous pouvons également utiliser la fonction persp() de pour créer un tracé de surface, qui offre une visualisation 3D de la distribution normale bivariée :

library(mnormt)

#make this example reproducible
set.seed(0)

#create bivariate normal distribution
x     <- seq(-3, 3, 0.1) 
y     <- seq(-3, 3, 0.1)
mu    <- c(0, 0)
sigma <- matrix(c(2, -1, -1, 2), nrow=2)
f     <- function(x, y) dmnorm(cbind(x, y), mu, sigma)
z     <- outer(x, y, f)

#create surface plot
persp(x, y, z, theta=-30, phi=25, expand=0.6, ticktype='detailed')

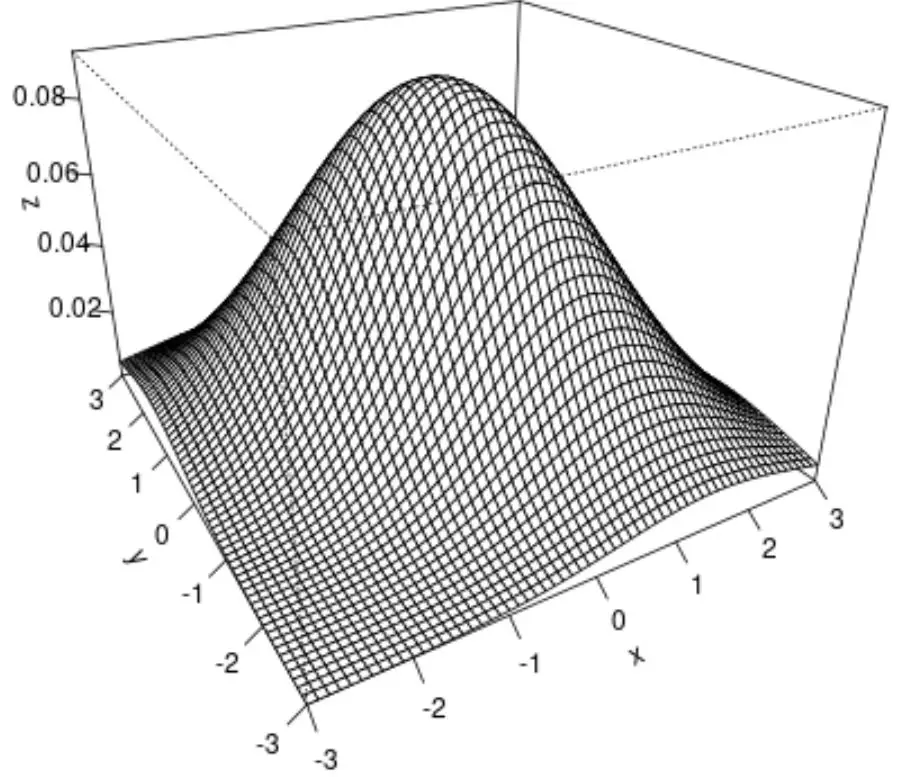
Voici ce que fait chaque argument de la fonction persp() :

• theta, phi : Définit les angles de la direction de visualisation.
• expand : Contrôle la taille de l’axe z.
• ticktype : Contrôle l’apparence des ticks sur les axes.

Le résultat final est un tracé de surface 3D de la distribution normale bivariée.

Ressources additionnelles

Les didacticiels suivants expliquent comment utiliser d’autres distributions de probabilité dans R :

Comment utiliser la distribution normale dans R
Comment utiliser la distribution binomiale dans R
Comment utiliser la distribution de Poisson dans R
Comment utiliser la distribution multinomiale dans R