Comment effectuer une analyse bivariée en Python : avec des exemples

Le terme analyse bivariée fait référence à l’analyse de deux variables. Vous pouvez vous en souvenir car le préfixe « bi » signifie « deux ».

Le but de l’analyse bivariée est de comprendre la relation entre deux variables

Il existe trois manières courantes d’effectuer une analyse bivariée :

1. Nuages de points

2. Coefficients de corrélation

3. Régression linéaire simple

L’exemple suivant montre comment effectuer chacun de ces types d’analyse bivariée en Python à l’aide du DataFrame pandas suivant qui contient des informations sur deux variables : (1) Heures passées à étudier et (2) Score d’examen obtenu par 20 étudiants différents :

import pandas as pd

#create DataFrame
df = pd.DataFrame({'hours': [1, 1, 1, 2, 2, 2, 3, 3, 3, 3,
                             3, 4, 4, 5, 5, 6, 6, 6, 7, 8],
                   'score': [75, 66, 68, 74, 78, 72, 85, 82, 90, 82,
                             80, 88, 85, 90, 92, 94, 94, 88, 91, 96]})

#view first five rows of DataFrame
df.head()

	hours	score
0	1	75
1	1	66
2	1	68
3	2	74
4	2	78

1. Nuages de points

Nous pouvons utiliser la syntaxe suivante pour créer un nuage de points des heures étudiées par rapport aux résultats de l’examen :

import matplotlib.pyplot as plt

#create scatterplot of hours vs. score
plt.scatter(df.hours, df.score)
plt.title('Hours Studied vs. Exam Score')
plt.xlabel('Hours Studied')
plt.ylabel('Exam Score')

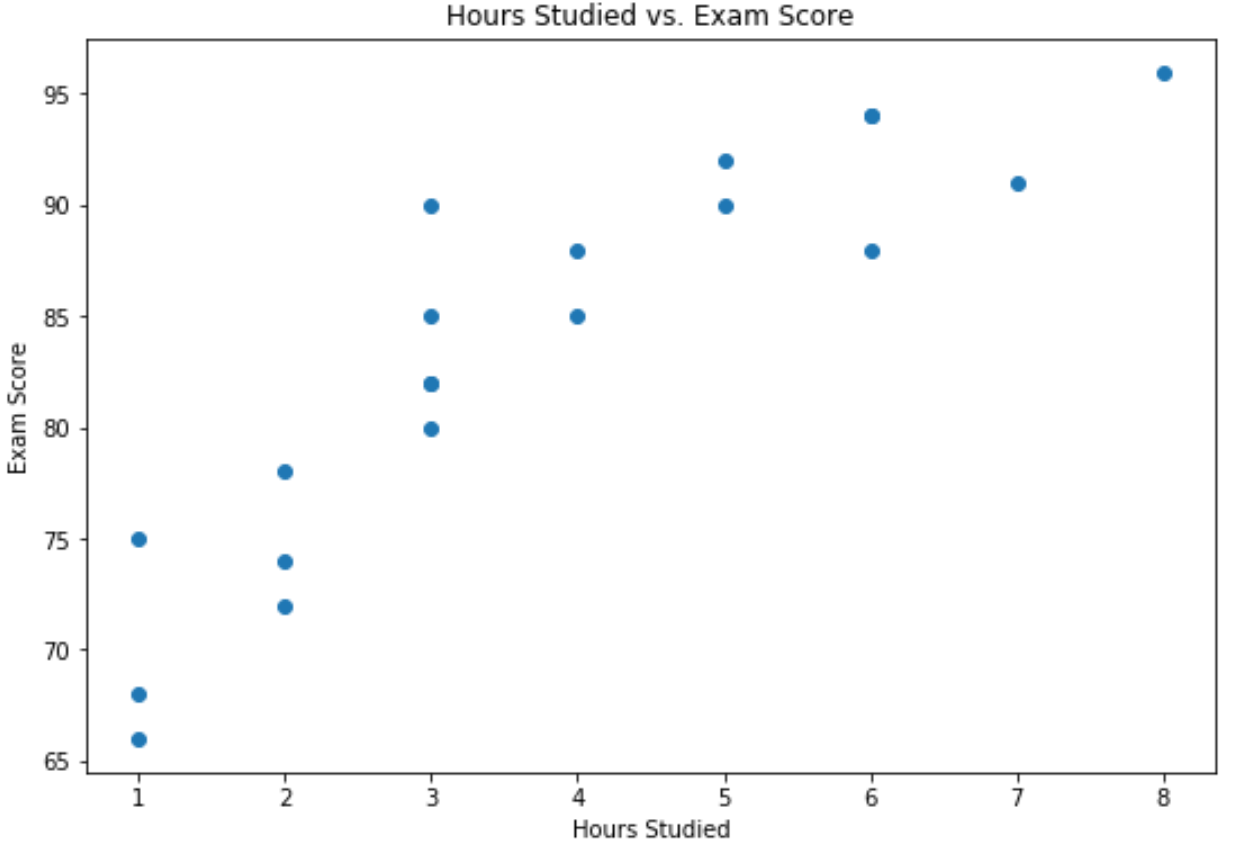
L’axe des x montre les heures étudiées et l’axe des y montre la note obtenue à l’examen.

Le graphique montre qu’il existe une relation positive entre les deux variables : à mesure que le nombre d’heures d’études augmente, les résultats aux examens ont également tendance à augmenter.

2. Coefficients de corrélation

Un coefficient de corrélation de Pearson est un moyen de quantifier la relation linéaire entre deux variables.

Nous pouvons utiliser la fonction corr() dans pandas pour créer une matrice de corrélation :

#create correlation matrix
df.corr()

	hours	score
hours	1.000000	0.891306
score	0.891306	1.000000

Le coefficient de corrélation s’avère être de 0,891 . Cela indique une forte corrélation positive entre les heures étudiées et la note obtenue à l’examen.

3. Régression linéaire simple

La régression linéaire simple est une méthode statistique que nous pouvons utiliser pour quantifier la relation entre deux variables.

Nous pouvons utiliser la fonction OLS() du package statsmodels pour ajuster rapidement un modèle de régression linéaire simple pour les heures étudiées et les résultats d’examen reçus :

import statsmodels.api as sm

#define response variable
y = df['score']

#define explanatory variable
x = df[['hours']]

#add constant to predictor variables
x = sm.add_constant(x)

#fit linear regression model
model = sm.OLS(y, x).fit()

#view model summary
print(model.summary())

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                  score   R-squared:                       0.794
Model:                            OLS   Adj. R-squared:                  0.783
Method:                 Least Squares   F-statistic:                     69.56
Date:                Mon, 22 Nov 2021   Prob (F-statistic):           1.35e-07
Time:                        16:15:52   Log-Likelihood:                -55.886
No. Observations:                  20   AIC:                             115.8
Df Residuals:                      18   BIC:                             117.8
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const         69.0734      1.965     35.149      0.000      64.945      73.202
hours          3.8471      0.461      8.340      0.000       2.878       4.816
==============================================================================
Omnibus:                        0.171   Durbin-Watson:                   1.404
Prob(Omnibus):                  0.918   Jarque-Bera (JB):                0.177
Skew:                           0.165   Prob(JB):                        0.915
Kurtosis:                       2.679   Cond. No.                         9.37
==============================================================================

L’équation de régression ajustée s’avère être :

Score d’examen = 69,0734 + 3,8471*(heures étudiées)

Cela nous indique que chaque heure supplémentaire étudiée est associée à une augmentation moyenne de 3,8471 de la note à l’examen.

Nous pouvons également utiliser l’équation de régression ajustée pour prédire le score qu’un étudiant recevra en fonction du nombre total d’heures étudiées.

Par exemple, un étudiant qui étudie pendant 3 heures devrait obtenir un score de 81,6147 :

• Score d’examen = 69,0734 + 3,8471*(heures étudiées)
• Score d’examen = 69,0734 + 3,8471*(3)
• Résultat de l’examen = 81,6147

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur l’analyse bivariée :

Une introduction à l’analyse bivariée
5 exemples de données bivariées dans la vie réelle
Une introduction à la régression linéaire simple
Une introduction au coefficient de corrélation de Pearson