L’hypothèse de variance constante : définition & Exemple

La régression linéaire est une technique que nous utilisons pour quantifier la relation entre une ou plusieurs variables prédictives et une variable de réponse .

L’une des hypothèses clés de la régression linéaire est que les résidus ont une variance constante à chaque niveau de la ou des variables prédictives.

Si cette hypothèse n’est pas vérifiée, les résidus souffriraient d’ hétéroscédasticité . Lorsque cela se produit, les estimations des coefficients du modèle deviennent peu fiables.

Comment évaluer la variance constante

La manière la plus courante de déterminer si les résidus d’un modèle de régression ont une variance constante consiste à créer un graphique des valeurs ajustées par rapport aux résidus .

Il s’agit d’un type de tracé qui affiche les valeurs ajustées du modèle de régression le long de l’axe des x et les résidus de ces valeurs ajustées le long de l’axe des y.

Si la répartition des résidus est à peu près égale à chaque niveau des valeurs ajustées, nous disons que l’hypothèse de variance constante est satisfaite.

Autrement, si la dispersion des résidus augmente ou diminue systématiquement, cette hypothèse est probablement violée.

Remarque : Ce type de tracé ne peut être créé qu’après avoir ajusté un modèle de régression à l’ensemble de données.

Le graphique suivant montre un exemple de graphique des valeurs ajustées par rapport aux valeurs résiduelles qui affiche une variance constante :

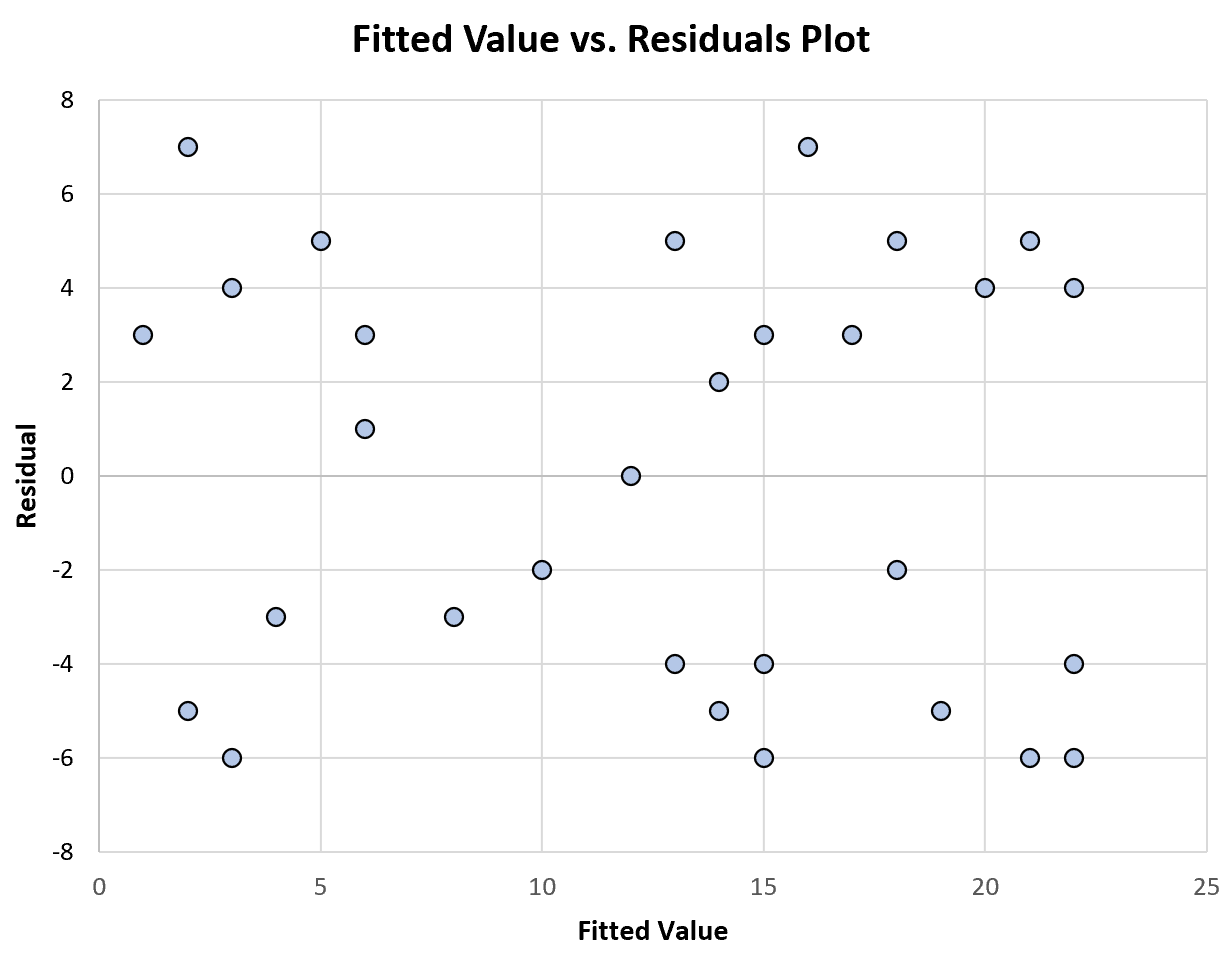
Remarquez comment les résidus sont dispersés de manière aléatoire autour de zéro, sans motif particulier, avec une variance à peu près constante à chaque niveau des valeurs ajustées.

Le graphique suivant montre un exemple de graphique des valeurs ajustées par rapport aux valeurs résiduelles qui affiche une variance non constante :

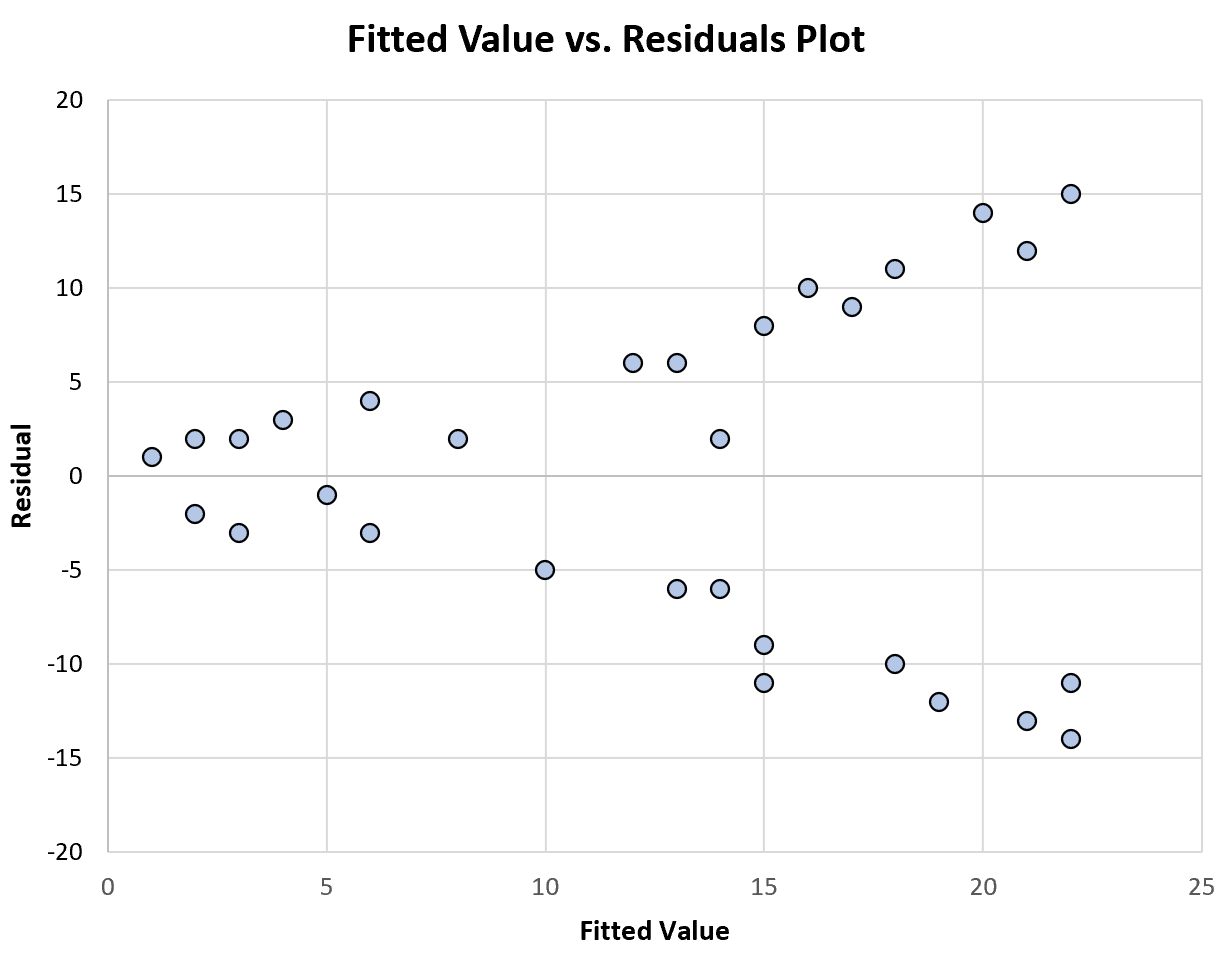
Notez que la répartition des résidus s’agrandit à mesure que les valeurs ajustées augmentent. C’est un signe typique de variance non constante.

Cela nous indique que notre modèle de régression souffre d’une variance non constante des résidus et que les estimations des coefficients du modèle ne sont donc pas fiables.

Comment réparer une violation de la variance constante

Si l’hypothèse de variance constante n’est pas respectée, la façon la plus courante de résoudre ce problème consiste à transformer la variable de réponse à l’aide de l’une des trois transformations :

1. Log Transformation : Transformez la variable de réponse de y en log(y)

2. Transformation racine carrée : transformez la variable de réponse de y en √ y

3. Transformation de racine cubique : transformez la variable de réponse de y en y ^1/3

En effectuant ces transformations, le problème de la variance non constante disparaît généralement.

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur la régression linéaire et l’analyse résiduelle :

Introduction à la régression linéaire simple
Introduction à la régression linéaire multiple
Les quatre hypothèses de la régression linéaire
Que sont les résidus dans les statistiques ?