Qu’est-ce que la multicolinéarité parfaite ? (Définition & Exemples)

En statistique, la multicolinéarité se produit lorsque deux ou plusieurs variables prédictives sont fortement corrélées les unes aux autres, de sorte qu’elles ne fournissent pas d’informations uniques ou indépendantes dans le modèle de régression.

Si le degré de corrélation est suffisamment élevé entre les variables, cela peut poser des problèmes lors de l’ajustement et de l’interprétation du modèle de régression.

Le cas le plus extrême de multicolinéarité est appelé multicolinéarité parfaite . Cela se produit lorsqu’au moins deux variables prédictives ont une relation linéaire exacte entre elles.

Par exemple, supposons que nous ayons l’ensemble de données suivant :

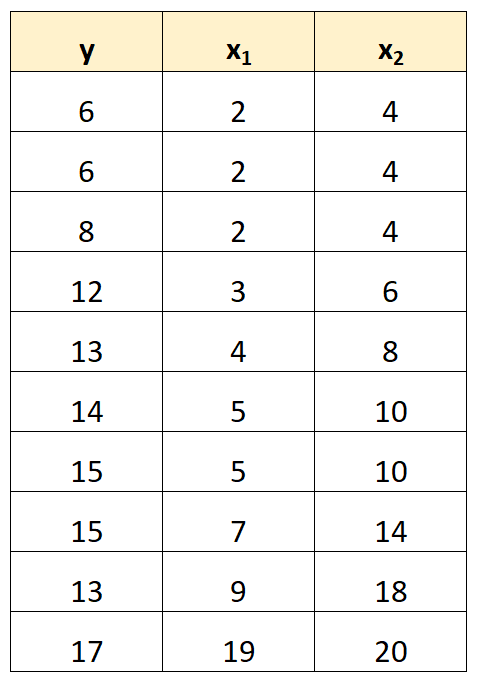
Notez que les valeurs de la variable prédictive x ₂ sont simplement les valeurs de x ₁ multipliées par 2.

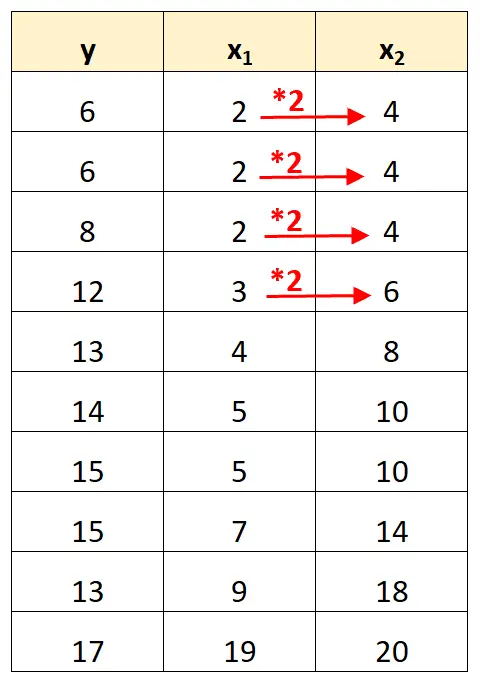
Ceci est un exemple de multicolinéarité parfaite .

Le problème de la multicolinéarité parfaite

Lorsqu’une multicolinéarité parfaite est présente dans un ensemble de données, la méthode des moindres carrés ordinaires est incapable de produire des estimations des coefficients de régression.

En effet, il n’est pas possible d’estimer l’effet marginal d’une variable prédictive (x ₁ ) sur la variable de réponse (y) tout en maintenant constante une autre variable prédictive (x ₂ ) car x ₂ se déplace toujours exactement lorsque x ₁ se déplace.

En bref, une multicolinéarité parfaite rend impossible l’estimation d’une valeur pour chaque coefficient dans un modèle de régression.

Comment gérer une multicolinéarité parfaite

Le moyen le plus simple de gérer une multicolinéarité parfaite consiste à supprimer l’une des variables qui a une relation linéaire exacte avec une autre variable.

Par exemple, dans notre ensemble de données précédent, nous pourrions simplement supprimer x ₂ comme variable prédictive.

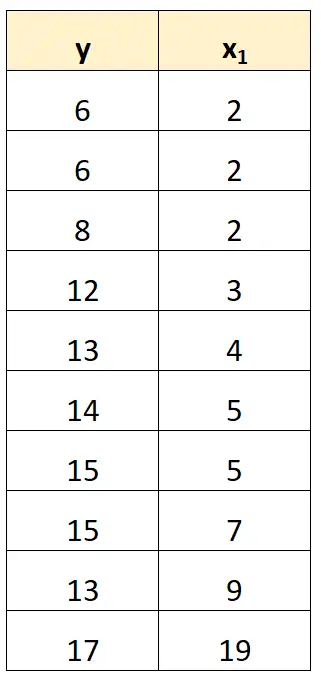
Nous ajusterions ensuite un modèle de régression en utilisant x ₁ comme variable prédictive et y comme variable de réponse.

Exemples de multicolinéarité parfaite

Les exemples suivants montrent les trois scénarios les plus courants de multicolinéarité parfaite dans la pratique.

1. Une variable prédictive est un multiple d’une autre

Supposons que nous voulions utiliser « taille en centimètres » et « taille en mètres » pour prédire le poids d’une certaine espèce de dauphin.

Voici à quoi pourrait ressembler notre ensemble de données :

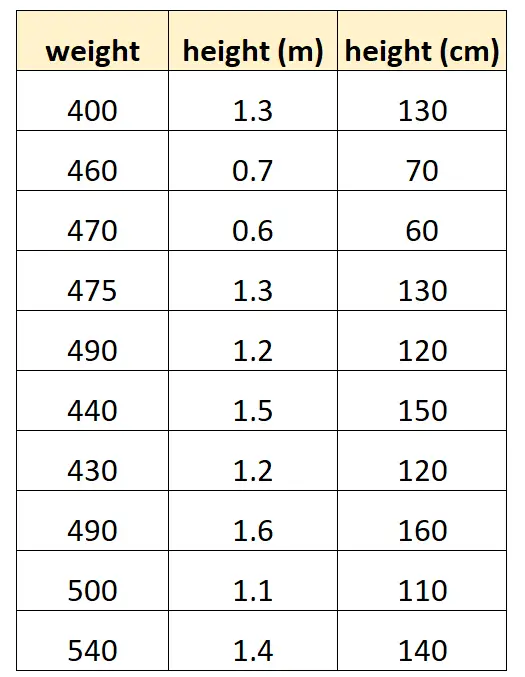
Notez que la valeur de « hauteur en centimètres » est simplement égale à « hauteur en mètres » multipliée par 100. Il s’agit d’un cas de multicolinéarité parfaite.

Si nous essayons d’ajuster un modèle de régression linéaire multiple dans R à l’aide de cet ensemble de données, nous ne pourrons pas produire d’estimation de coefficient pour la variable prédictive « mètres » :

#define data
df <- data.frame(weight=c(400, 460, 470, 475, 490, 440, 430, 490, 500, 540),
                 m=c(1.3, .7, .6, 1.3, 1.2, 1.5, 1.2, 1.6, 1.1, 1.4),
                 cm=c(130, 70, 60, 130, 120, 150, 120, 160, 110, 140))

#fit multiple linear regression model
model <- lm(weight~m+cm, data=df)

#view summary of model
summary(model)

Call:
lm(formula = weight ~ m + cm, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-70.501 -25.501   5.183  19.499  68.590 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  458.676     53.403   8.589 2.61e-05 ***
m              9.096     43.473   0.209    0.839    
cm                NA         NA      NA       NA    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 41.9 on 8 degrees of freedom
Multiple R-squared:  0.005442,	Adjusted R-squared:  -0.1189 
F-statistic: 0.04378 on 1 and 8 DF,  p-value: 0.8395

2. Une variable prédictive est une version transformée d’une autre

Supposons que nous souhaitions utiliser des « points » et des « points échelonnés » pour prédire la note des joueurs de basket-ball.

Supposons que la variable « points mis à l’échelle » soit calculée comme :

Points mis à l’échelle = (points – μ _points ) / σ _points

Voici à quoi pourrait ressembler notre ensemble de données :

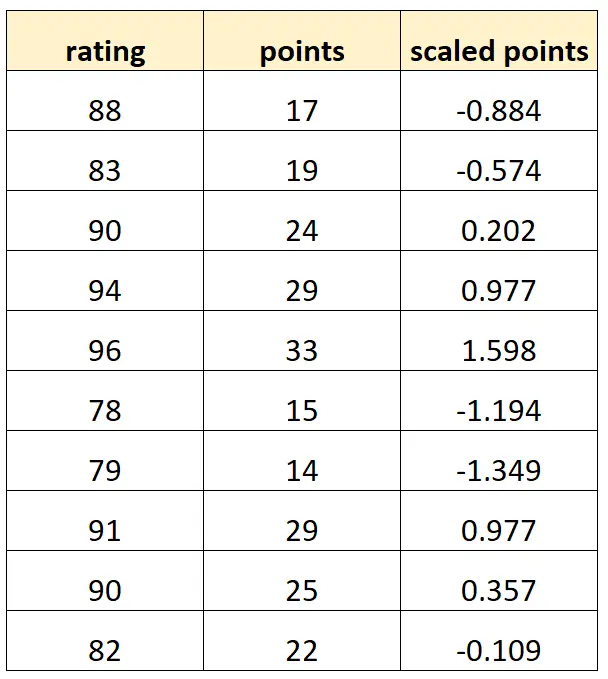
Notez que chaque valeur de « points mis à l’échelle » est simplement une version standardisée de « points ». Il s’agit d’un cas de multicolinéarité parfaite.

Si nous essayons d’ajuster un modèle de régression linéaire multiple dans R à l’aide de cet ensemble de données, nous ne pourrons pas produire d’estimation de coefficient pour la variable prédictive « points mis à l’échelle » :

#define data
df <- data.frame(rating=c(88, 83, 90, 94, 96, 78, 79, 91, 90, 82),
                 pts=c(17, 19, 24, 29, 33, 15, 14, 29, 25, 22))

df$scaled_pts <- (df$pts - mean(df$pts)) / sd(df$pts)

#fit multiple linear regression model
model <- lm(rating~pts+scaled_pts, data=df)

#view summary of model
summary(model)

Call:
lm(formula = rating ~ pts + scaled_pts, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.4932 -1.3941 -0.2935  1.3055  5.8412 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  67.4218     3.5896  18.783 6.67e-08 ***
pts           0.8669     0.1527   5.678 0.000466 ***
scaled_pts        NA         NA      NA       NA    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.953 on 8 degrees of freedom
Multiple R-squared:  0.8012,	Adjusted R-squared:  0.7763 
F-statistic: 32.23 on 1 and 8 DF,  p-value: 0.0004663

3. Le piège variable factice

Un autre scénario dans lequel une multicolinéarité parfaite peut se produire est connu sous le nom de piège à variables factices . C’est à ce moment-là que nous voulons utiliser une variable catégorielle dans un modèle de régression et la convertir en une « variable factice » qui prend les valeurs de 0, 1, 2, etc.

Par exemple, supposons que nous souhaitions utiliser les variables prédictives « âge » et « état civil » pour prédire le revenu :

Pour utiliser « l’état civil » comme variable prédictive, nous devons d’abord le convertir en variable muette.

Pour ce faire, nous pouvons laisser « Célibataire » comme valeur de base, car cela se produit le plus souvent, et attribuer des valeurs de 0 ou 1 à « Marié » et « Divorce » comme suit :

Une erreur serait de créer trois nouvelles variables fictives comme suit :

Dans ce cas, la variable « Célibataire » est une combinaison linéaire parfaite des variables « Marié » et « Divorcé ». Ceci est un exemple de multicolinéarité parfaite.

Si nous essayons d’ajuster un modèle de régression linéaire multiple dans R à l’aide de cet ensemble de données, nous ne pourrons pas produire une estimation de coefficient pour chaque variable prédictive :

#define data
df <- data.frame(income=c(45, 48, 54, 57, 65, 69, 78, 83, 98, 104, 107),
                 age=c(23, 25, 24, 29, 38, 36, 40, 59, 56, 64, 53),
                 single=c(1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0),
                 married=c(0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1),
                 divorced=c(0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0))

#fit multiple linear regression model
model <- lm(income~age+single+married+divorced, data=df)

#view summary of model
summary(model)

Call:
lm(formula = income ~ age + single + married + divorced, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-9.7075 -5.0338  0.0453  3.3904 12.2454 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)   
(Intercept)  16.7559    17.7811   0.942  0.37739   
age           1.4717     0.3544   4.152  0.00428 **
single       -2.4797     9.4313  -0.263  0.80018   
married           NA         NA      NA       NA   
divorced     -8.3974    12.7714  -0.658  0.53187   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 8.391 on 7 degrees of freedom
Multiple R-squared:  0.9008,	Adjusted R-squared:  0.8584 
F-statistic:  21.2 on 3 and 7 DF,  p-value: 0.0006865

Ressources additionnelles

Un guide sur la multicolinéarité et le VIF en régression
Comment calculer VIF dans R
Comment calculer VIF en Python
Comment calculer le VIF dans Excel