Quand devriez-vous utiliser la corrélation ? (Explication & Exemples)

La corrélation est utilisée pour mesurer l’association linéaire entre deux variables.

Un coefficient de corrélation prend toujours une valeur comprise entre -1 et 1 où :

• -1 indique une corrélation linéaire parfaitement négative entre deux variables
• 0 indique aucune corrélation linéaire entre deux variables
• 1 indique une corrélation linéaire parfaitement positive entre deux variables

Une question que les étudiants se posent souvent est la suivante : quand dois-je utiliser la corrélation ?

La réponse courte : utilisez la corrélation lorsque vous souhaitez quantifier la relation linéaire entre deux variables et qu’aucune des variables ne représente une variable de réponse ou de « résultat » .

Les exemples suivants illustrent quand vous devez et ne devez pas utiliser la corrélation dans la pratique.

Exemple 1 : Quand utiliser la corrélation

Supposons qu’un professeur souhaite comprendre la relation linéaire entre les résultats aux examens de mathématiques et les résultats aux examens de sciences des étudiants de sa classe.

Par exemple, les élèves qui obtiennent de bons résultats à l’examen de mathématiques obtiennent-ils également de bons résultats à l’examen de sciences ? Ou les élèves qui obtiennent des résultats élevés en mathématiques ont-ils tendance à avoir des résultats faibles en sciences ?

Dans ce scénario, il pourrait calculer la corrélation entre les résultats des examens de mathématiques et ceux des examens de sciences, car il souhaite simplement comprendre la relation linéaire entre les deux variables et aucune des deux variables ne peut être considérée comme une variable de réponse.

Supposons qu’il calcule le coefficient de corrélation de Pearson et trouve qu’il est r = 0,78. Il s’agit d’une forte corrélation positive, ce qui signifie que les élèves qui obtiennent de bons résultats en mathématiques ont également tendance à obtenir de bons résultats en sciences.

Exemple 2 : Quand ne pas utiliser la corrélation

Supposons qu’un service marketing d’une entreprise souhaite quantifier l’impact des dépenses publicitaires sur les revenus totaux.

Par exemple, pour chaque dollar supplémentaire dépensé en publicité, combien de revenus supplémentaires l’entreprise peut-elle espérer gagner ?

Dans ce scénario, le ministère doit utiliser un modèle de régression linéaire pour quantifier la relation entre les dépenses publicitaires et les revenus totaux, car la variable « revenus » est la variable de réponse.

Supposons que le service applique un modèle de régression linéaire simple et trouve que l’équation suivante décrit le mieux la relation entre les dépenses publicitaires et les revenus totaux :

Revenu total = 145,4 + 0,34*(dépenses publicitaires)

Nous interpréterions cela comme signifiant que chaque dollar supplémentaire dépensé en publicité entraîne une augmentation moyenne de 0,34 $ des revenus totaux.

Précautions concernant l’utilisation de la corrélation

Il est important de noter que la corrélation ne peut être utilisée que pour quantifier la relation linéaire entre deux variables.

Cependant, dans certaines circonstances, un coefficient de corrélation ne sera pas en mesure de capturer efficacement une relation entre deux variables partageant une relation non linéaire.

Par exemple, supposons que nous créions le nuage de points suivant pour visualiser la relation entre deux variables :

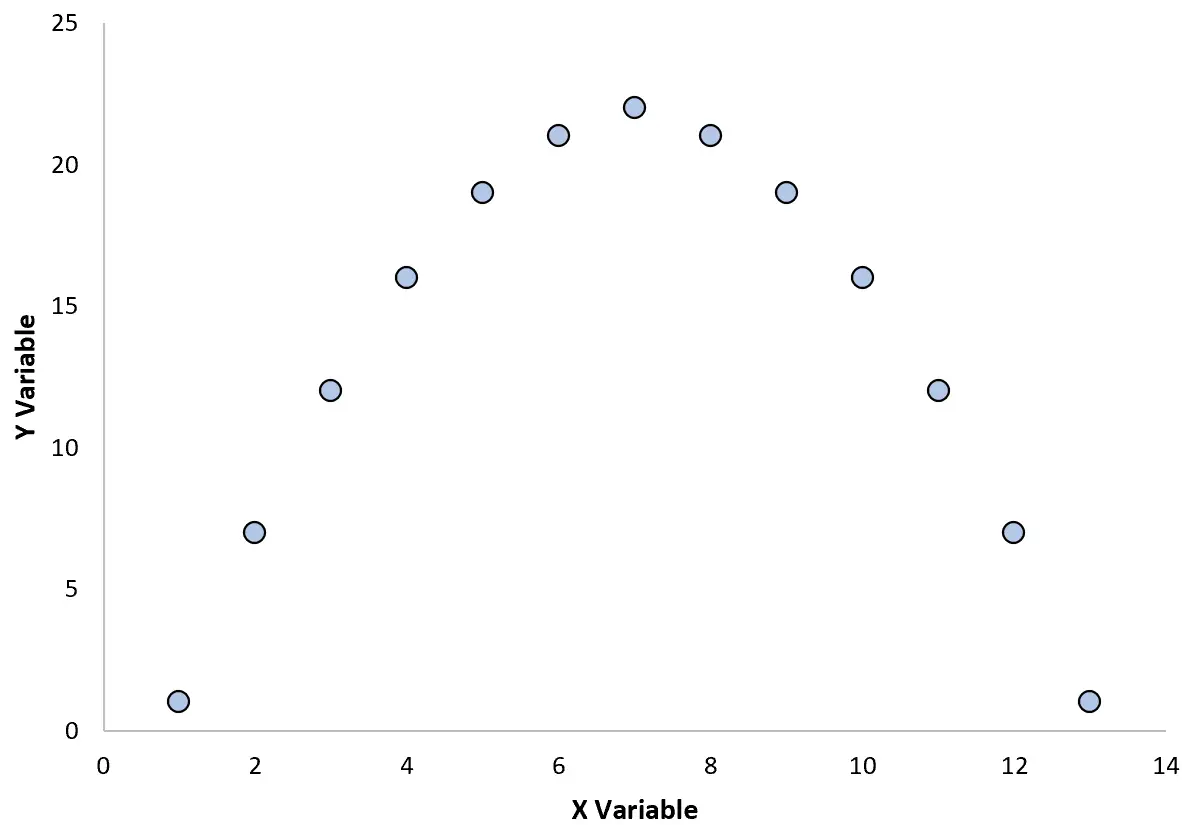
Si l’on calcule le coefficient de corrélation entre ces deux variables, il s’avère être r = 0. Cela signifie qu’il n’y a pas de relation linéaire entre les deux variables.

Cependant, à partir du graphique, nous pouvons voir que les deux variables ont effectivement une relation – il s’agit simplement d’une relation quadratique au lieu d’une relation linéaire.

Ainsi, lorsque vous calculez la corrélation entre deux variables, gardez à l’esprit qu’il peut également être utile de créer un nuage de points pour visualiser la relation entre les variables.

Même si deux variables n’ont pas de relation linéaire, il est possible qu’elles aient une relation non linéaire qui serait révélée dans un nuage de points.

Ressources additionnelles

Les didacticiels suivants expliquent plus en détail comment la corrélation est utilisée dans différentes circonstances :

6 exemples de corrélation dans la vie réelle
Qu’est-ce qui est considéré comme une corrélation « forte » ?
Corrélation vs association : quelle est la différence ?
Corrélation vs régression : quelle est la différence ?