Corrélation vs association : quelle est la différence ?

Deux termes parfois utilisés de manière interchangeable sont corrélation et association . Cependant, dans le domaine des statistiques, ces deux termes ont des significations légèrement différentes.

En particulier, lorsque nous utilisons le mot corrélation , nous parlons généralement du coefficient de corrélation de Pearson . Il s’agit d’une mesure de l’association linéaire entre deux variables aléatoires X et Y. Elle a une valeur comprise entre -1 et 1 où :

• -1 indique une corrélation linéaire parfaitement négative entre deux variables
• 0 indique aucune corrélation linéaire entre deux variables
• 1 indique une corrélation linéaire parfaitement positive entre deux variables

À l’inverse, lorsque les statisticiens utilisent le mot association , ils peuvent parler de toute relation entre deux variables, qu’elle soit linéaire ou non linéaire.

Pour illustrer cette idée, considérons les exemples suivants.

Visualisation de la corrélation et de l’association avec des nuages de points

Nous utilisons deux mots pour décrire la corrélation entre deux variables aléatoires :

1 direction

• Positif : deux variables aléatoires ont une corrélation positive si Y a tendance à augmenter à mesure que X augmente.
• Négatif : deux variables aléatoires ont une corrélation négative si Y a tendance à diminuer à mesure que X augmente.

2. Force

• Faible : deux variables aléatoires ont une faible corrélation si les points d’un nuage de points sont faiblement dispersés.
• Fort : deux variables aléatoires ont une forte corrélation si les points d’un nuage de points sont étroitement regroupés.

Les nuages de points suivants illustrent des exemples de chaque type de corrélation :

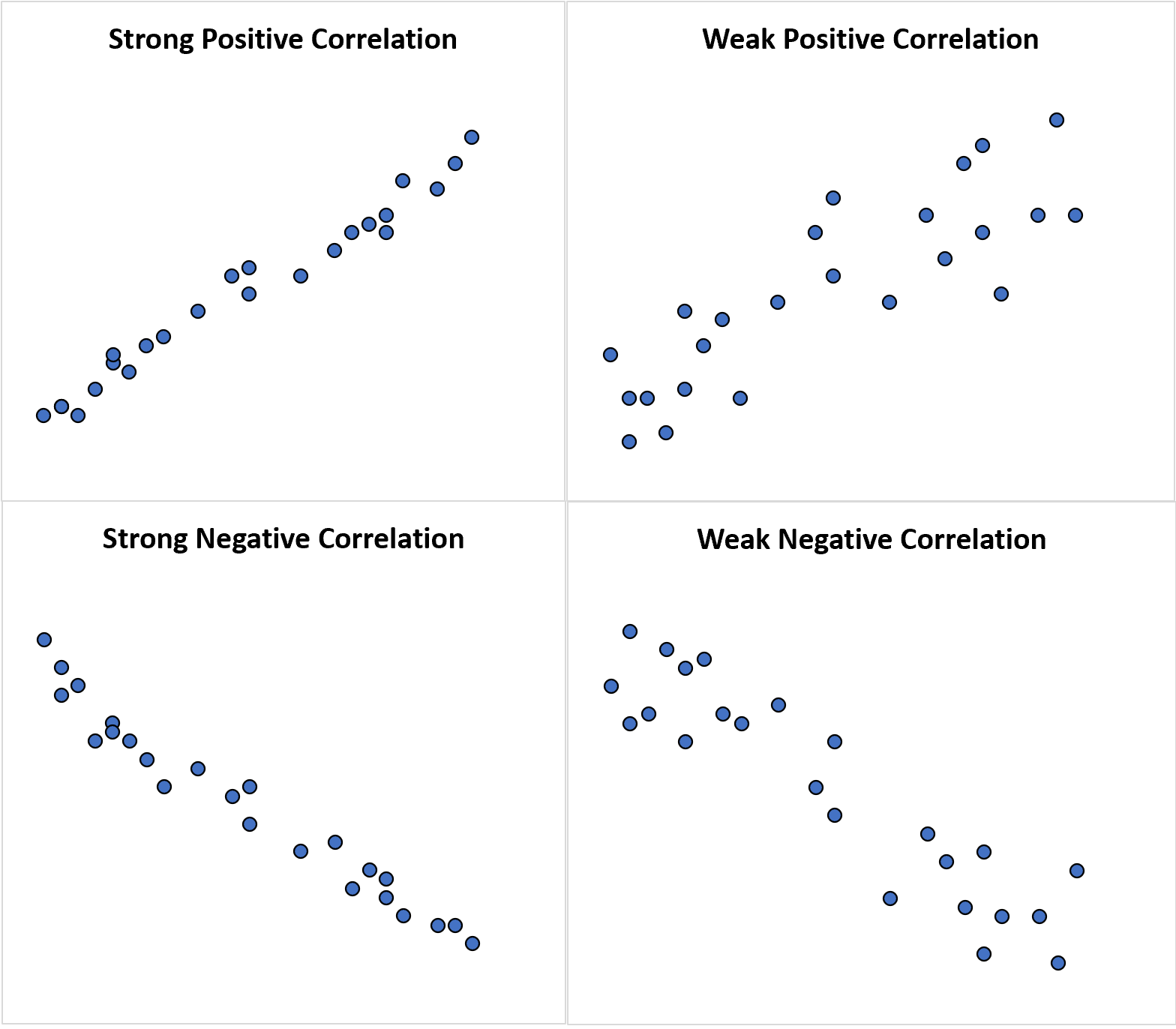
Par rapport à la corrélation, le mot association peut nous dire s’il existe ou non une relation entre deux variables aléatoires : linéaire ou non linéaire.

Les nuages de points suivants illustrent quelques exemples :

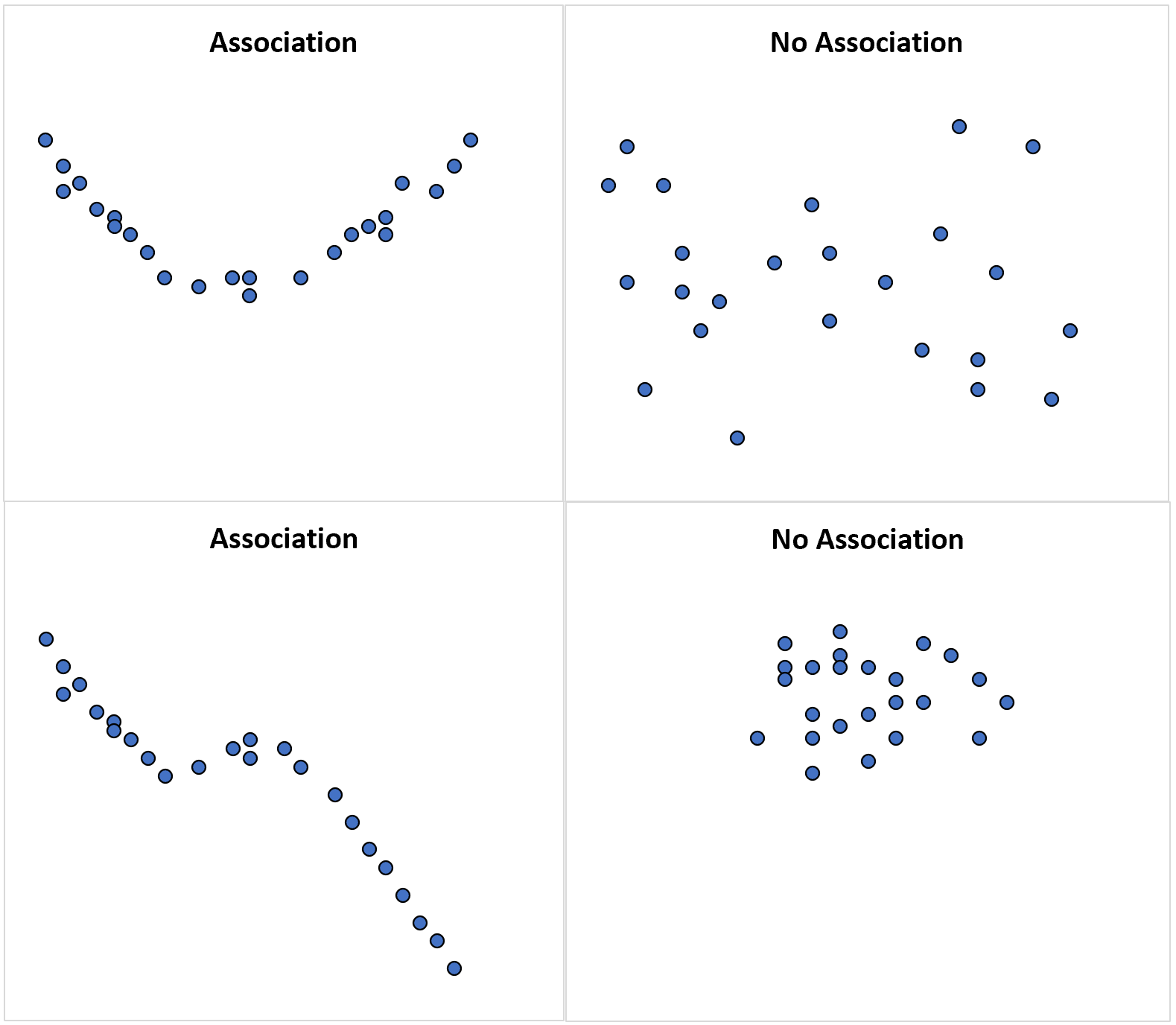
Le nuage de points dans le coin supérieur gauche illustre une relation quadratique entre deux variables aléatoires, ce qui signifie qu’il existe une association entre les deux variables mais qu’elle n’est pas linéaire.

Si nous calculions la corrélation entre les deux variables, elle serait probablement proche de zéro car il n’y a pas de relation linéaire entre elles.

Cependant, le simple fait de savoir que la corrélation entre les deux variables est nulle peut être trompeur car cela cache le fait qu’il existe plutôt une relation non linéaire.

Corrélation vs association : un résumé

Les termes corrélation et association présentent les similitudes et les différences suivantes :

Similitudes:

• Les deux termes sont utilisés pour décrire s’il existe ou non une relation entre deux variables aléatoires.
• Les deux termes peuvent utiliser des nuages de points pour analyser la relation entre deux variables aléatoires.

Différences:

• La corrélation peut seulement nous dire si deux variables aléatoires ont une relation linéaire tandis que l’association peut nous dire si deux variables aléatoires ont une relation linéaire ou non linéaire.
• La corrélation quantifie la relation entre deux variables aléatoires en utilisant un nombre compris entre -1 et 1, mais l’association n’utilise pas de nombre spécifique pour quantifier une relation.

Ressources additionnelles

Une introduction au coefficient de corrélation de Pearson
Une introduction aux nuages de points
Corrélation vs régression : quelle est la différence ?