Comment interpréter les tracés de diagnostic dans R

Les modèles de régression linéaire sont utilisés pour décrire la relation entre une ou plusieurs variables prédictives et une variable de réponse.

Cependant, une fois que nous avons ajusté un modèle de régression, il est judicieux de produire également des graphiques de diagnostic pour analyser les résidus du modèle et garantir qu’un modèle linéaire est approprié à utiliser pour les données particulières avec lesquelles nous travaillons.

Ce didacticiel explique comment créer et interpréter des tracés de diagnostic pour un modèle de régression donné dans R.

Exemple : créer et interpréter des tracés de diagnostic dans R

Supposons que nous ajustions un modèle de régression linéaire simple utilisant les « heures étudiées » pour prédire la « note à l’examen » des étudiants d’une certaine classe :

#create data frame
df <- data.frame(hours=c(1, 1, 2, 2, 2, 3, 3, 4, 4, 4, 4, 5, 5, 6),
                 score=c(67, 65, 68, 77, 73, 79, 81, 88, 80, 67, 84, 93, 90, 91)) 

#fit linear regression model
model = lm(score ~ hours, data=df)

Nous pouvons utiliser la commande plot() pour produire quatre tracés de diagnostic pour ce modèle de régression :

#produce diagnostic plots for regression model
plot(model)

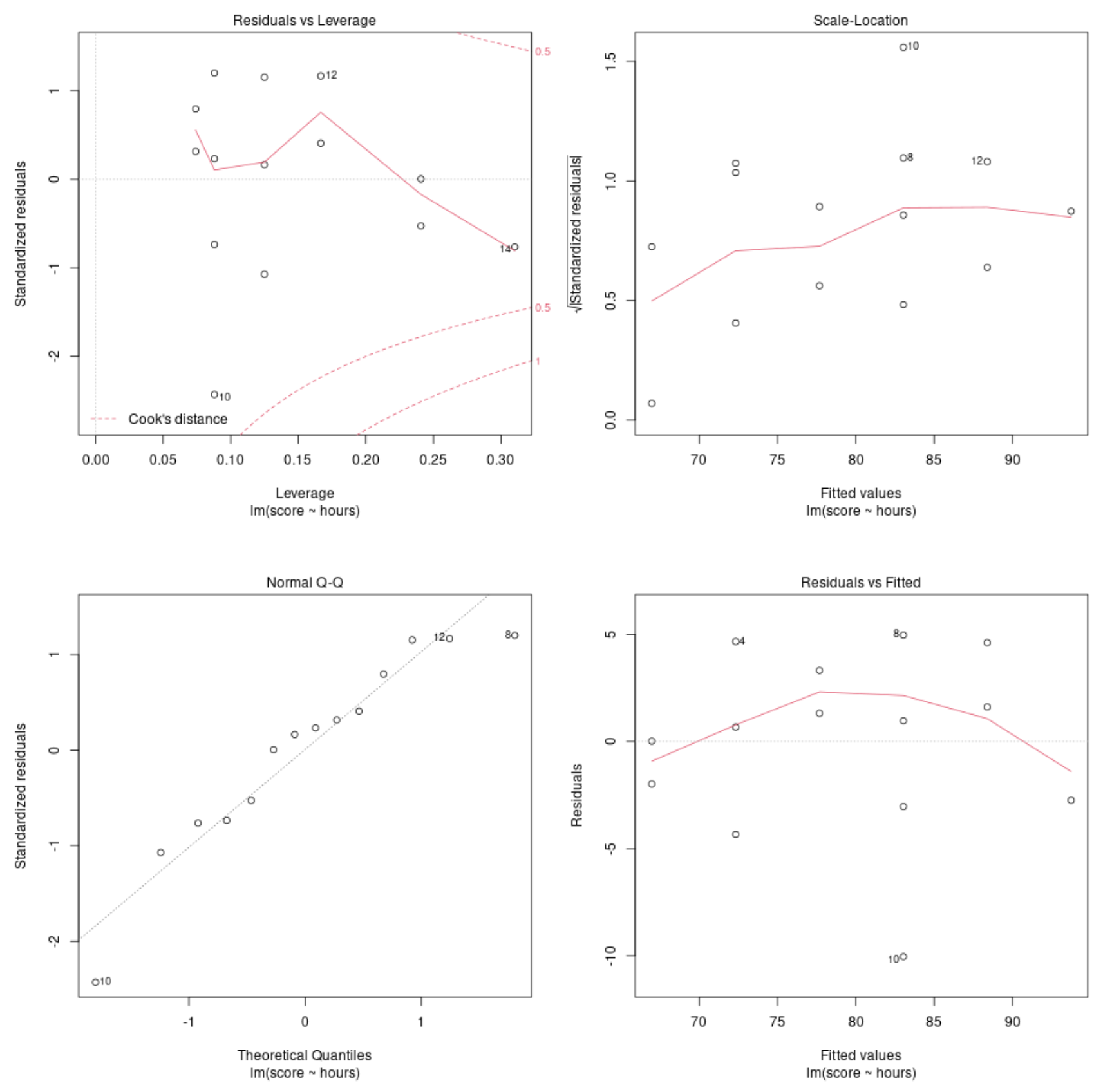
Graphique de diagnostic n° 1 : Graphique des résidus par rapport à l’effet de levier

Ce graphique est utilisé pour identifier les observations influentes. Si des points de ce graphique se situent en dehors de la distance de Cook (les lignes pointillées), il s’agit alors d’une observation influente.

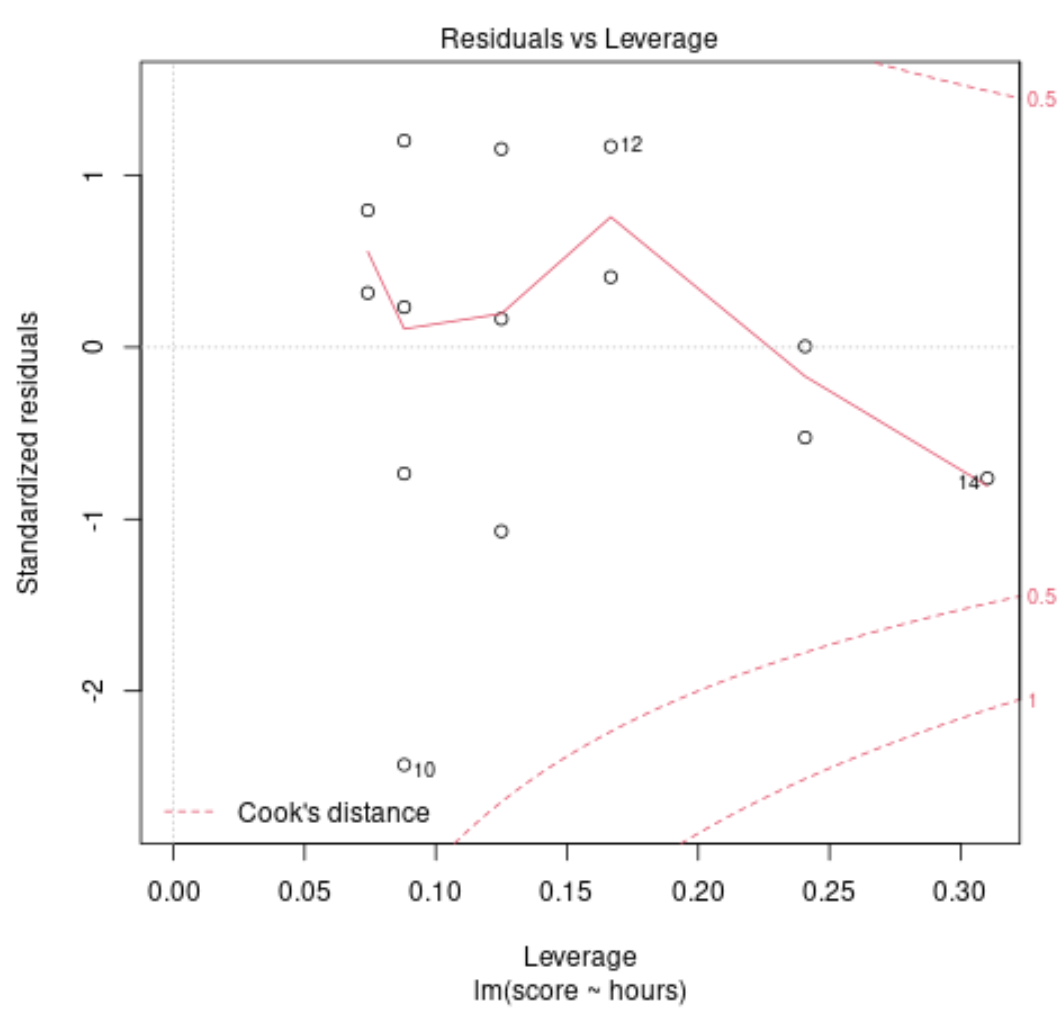
Dans notre exemple, nous pouvons voir que l’observation n°10 se trouve la plus proche de la limite de la distance de Cook, mais elle ne sort pas de la ligne pointillée. Cela signifie qu’il n’y a pas de points trop influents dans notre ensemble de données.

Tracé de diagnostic n°2 : tracé d’échelle et d’emplacement

Ce graphique est utilisé pour vérifier l’hypothèse d’égalité de variance (également appelée « homoscédasticité ») parmi les résidus de notre modèle de régression. Si la ligne rouge est à peu près horizontale sur le tracé, alors l’hypothèse d’une variance égale est probablement remplie.

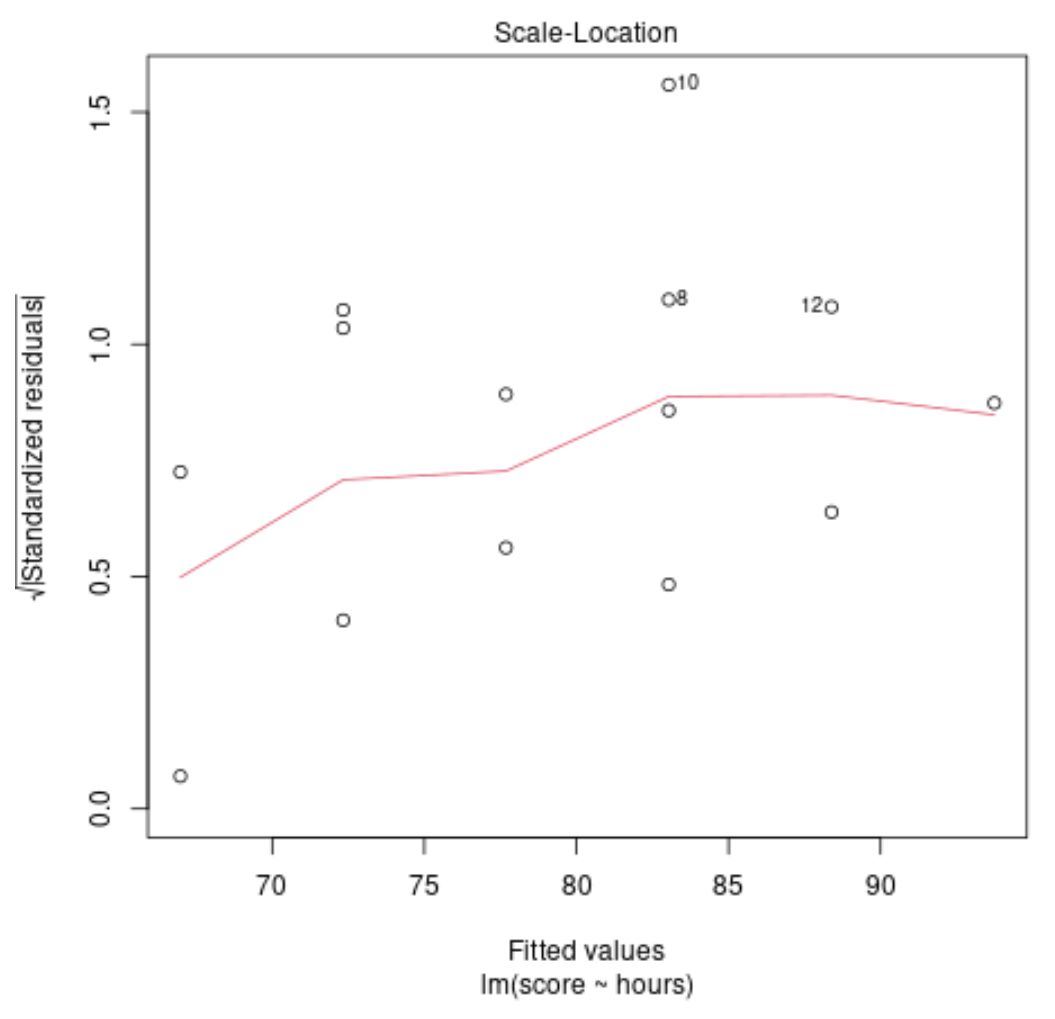
Dans notre exemple, nous pouvons voir que la ligne rouge n’est pas exactement horizontale sur le tracé, mais elle ne s’écarte pas trop énormément à aucun moment. Nous déclarons probablement que l’hypothèse d’une variance égale n’est pas violée dans ce cas.

Connexe : Comprendre l’hétéroscédasticité dans l’analyse de régression

Tracé de diagnostic n°3 : tracé QQ normal

Ce tracé est utilisé pour déterminer si les résidus du modèle de régression sont normalement distribués. Si les points de ce graphique se situent à peu près le long d’une ligne diagonale droite, alors nous pouvons supposer que les résidus sont normalement distribués.

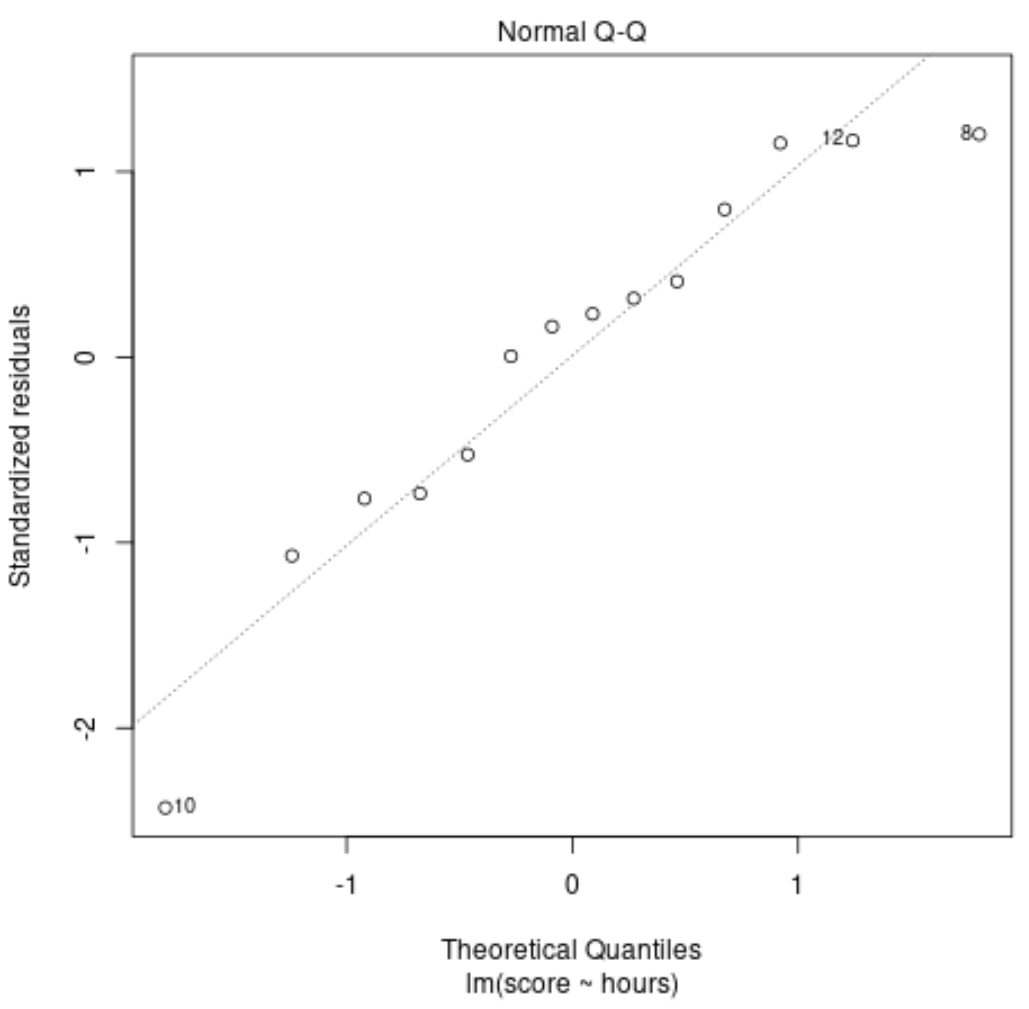
Dans notre exemple, nous pouvons voir que les points se situent à peu près le long de la ligne droite diagonale. Les observations n°10 et n°8 s’écartent un peu de la ligne aux extrémités, mais pas suffisamment pour déclarer que les résidus ne sont pas distribués normalement.

Tracé de diagnostic n°4 : Résidus vs tracé ajusté

Ce tracé est utilisé pour déterminer si les résidus présentent des modèles non linéaires. Si la ligne rouge au centre du tracé est à peu près horizontale, nous pouvons supposer que les résidus suivent un motif linéaire.

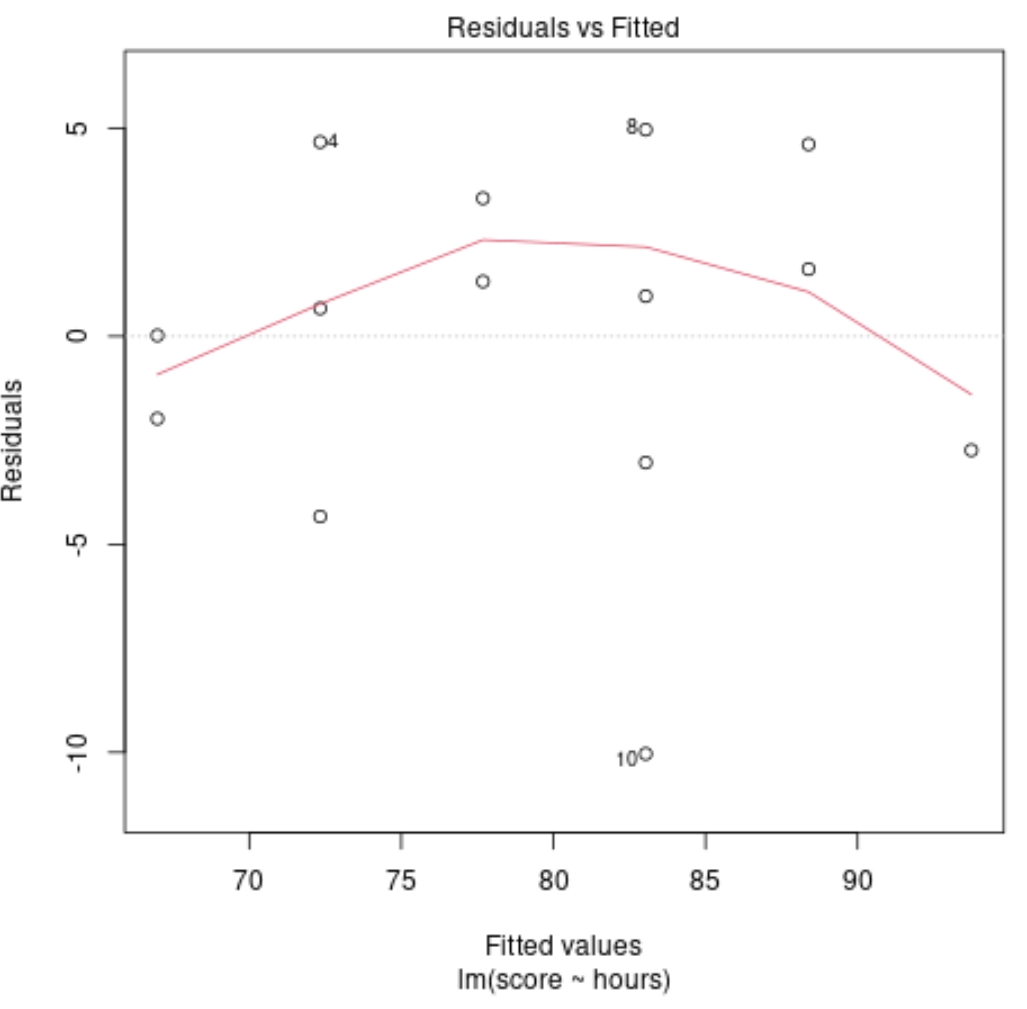
Dans notre exemple, nous pouvons voir que la ligne rouge s’écarte d’une ligne horizontale parfaite mais pas de manière importante. Nous déclarons probablement que les résidus suivent un modèle à peu près linéaire et qu’un modèle de régression linéaire est approprié pour cet ensemble de données.

Ressources additionnelles

Les quatre hypothèses de la régression linéaire
Que sont les résidus dans les statistiques ?
Comment créer un tracé résiduel dans R
Comment interpréter un tracé d’échelle et de localisation