Qu’est-ce que l’analyse univariée ? (Définition & #038; Exemple)

Le terme analyse univariée fait référence à l’analyse d’une variable. Vous pouvez vous en souvenir car le préfixe « uni » signifie « un ».

Le but de l’analyse univariée est de comprendre la distribution des valeurs pour une seule variable. Vous pouvez comparer ce type d’analyse avec ce qui suit :

• Analyse bivariée : L’analyse de deux variables.
• Analyse multivariée : analyse de deux variables ou plus.

Par exemple, supposons que nous ayons l’ensemble de données suivant :

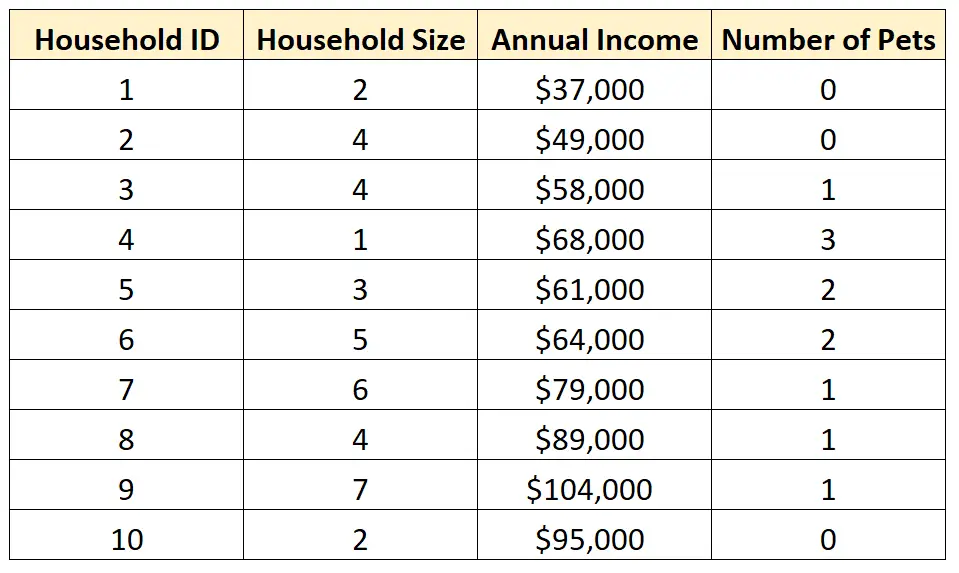
Nous pourrions choisir d’effectuer une analyse univariée sur l’une des variables individuelles de l’ensemble de données pour mieux comprendre sa distribution de valeurs.

Par exemple, nous pouvons choisir d’effectuer une analyse univariée sur la variable Taille du ménage :

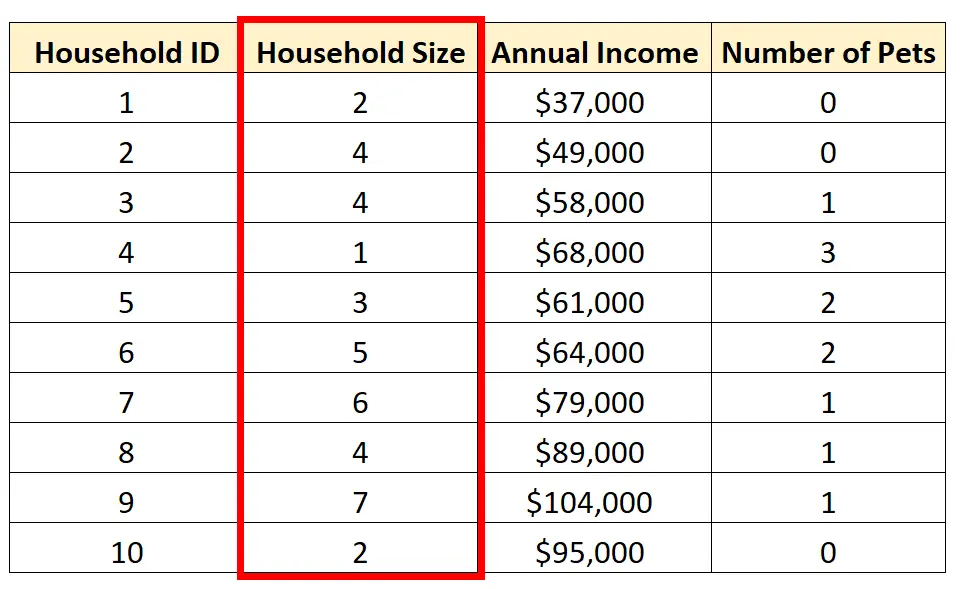
Il existe trois manières courantes d’effectuer une analyse univariée :

1. Statistiques récapitulatives

La manière la plus courante d’effectuer une analyse univariée consiste à décrire une variable à l’aide de statistiques récapitulatives .

Il existe deux types courants de statistiques récapitulatives :

• Mesures de tendance centrale : ces nombres décrivent où se trouve le centre d’un ensemble de données. Les exemples incluent la moyenne et la médiane .
• Mesures de dispersion : ces nombres décrivent la répartition des valeurs dans l’ensemble de données. Les exemples incluent l’ intervalle , l’intervalle interquartile , l’écart type et la variance .

2. Distributions de fréquences

Une autre façon d’effectuer une analyse univariée consiste à créer une distribution de fréquence , qui décrit la fréquence à laquelle différentes valeurs apparaissent dans un ensemble de données.

3. Graphiques

Une autre façon d’effectuer une analyse univariée consiste à créer des graphiques pour visualiser la distribution des valeurs pour une certaine variable.

Les exemples courants incluent :

• Boîtes à moustaches
• Histogrammes
• Courbes de densité
• Camemberts

Les exemples suivants montrent comment effectuer chaque type d’analyse univariée à l’aide de la variable Taille du ménage de notre ensemble de données mentionné précédemment :

Statistiques récapitulatives

Nous pouvons calculer les mesures suivantes de la tendance centrale de la taille du ménage :

• Moyenne (la valeur moyenne): 3,8
• Médiane (la valeur moyenne): 4

Ces valeurs nous donnent une idée de l’endroit où se situe la valeur « centrale ».

On peut également calculer les mesures de dispersion suivantes :

• Plage (la différence entre le max et le min): 6
• Échelle interquartile (la répartition des 50 % moyens des valeurs) : 2,5
• Écart type (une mesure moyenne de la propagation) : 1,87

Ces valeurs nous donnent une idée de la répartition des valeurs de cette variable.

Fréquence des distributions

Nous pouvons également créer le tableau de distribution de fréquence suivant pour résumer la fréquence à laquelle différentes valeurs se produisent :

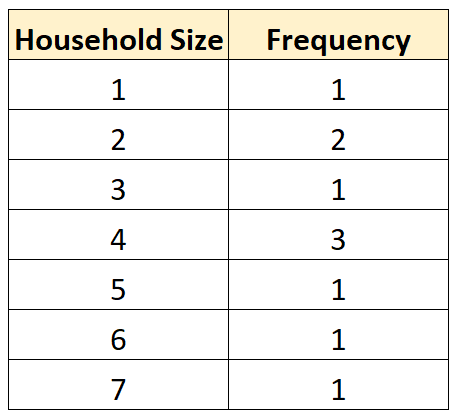
Cela nous permet de constater rapidement que la taille du ménage la plus fréquente est de 4 personnes .

Ressource : Vous pouvez utiliser ce calculateur de fréquence pour produire automatiquement une distribution de fréquence pour n’importe quelle variable.

Graphiques

Nous pouvons créer les graphiques suivants pour nous aider à visualiser la distribution des valeurs pour la taille du ménage :

1. Boîte à moustaches

Un boxplot est un graphique qui montre le résumé à cinq chiffres d’un ensemble de données.

Le résumé en cinq chiffres comprend :

• La valeur minimale
• Le premier quartile
• La valeur médiane
• Le troisième quartile
• La valeur maximale

Voici à quoi ressemblerait un boxplot pour la variable Taille du ménage :

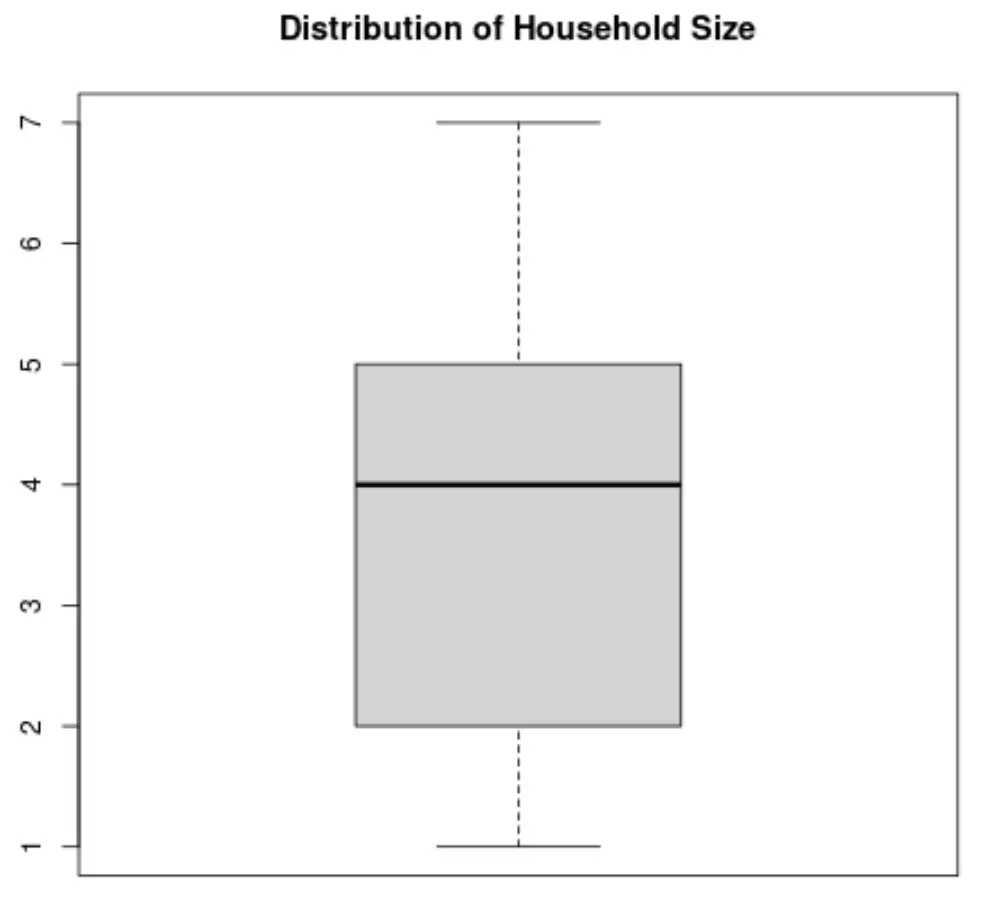
Ressource : Vous pouvez utiliser ce générateur de boxplot pour produire automatiquement un boxplot pour n’importe quelle variable.

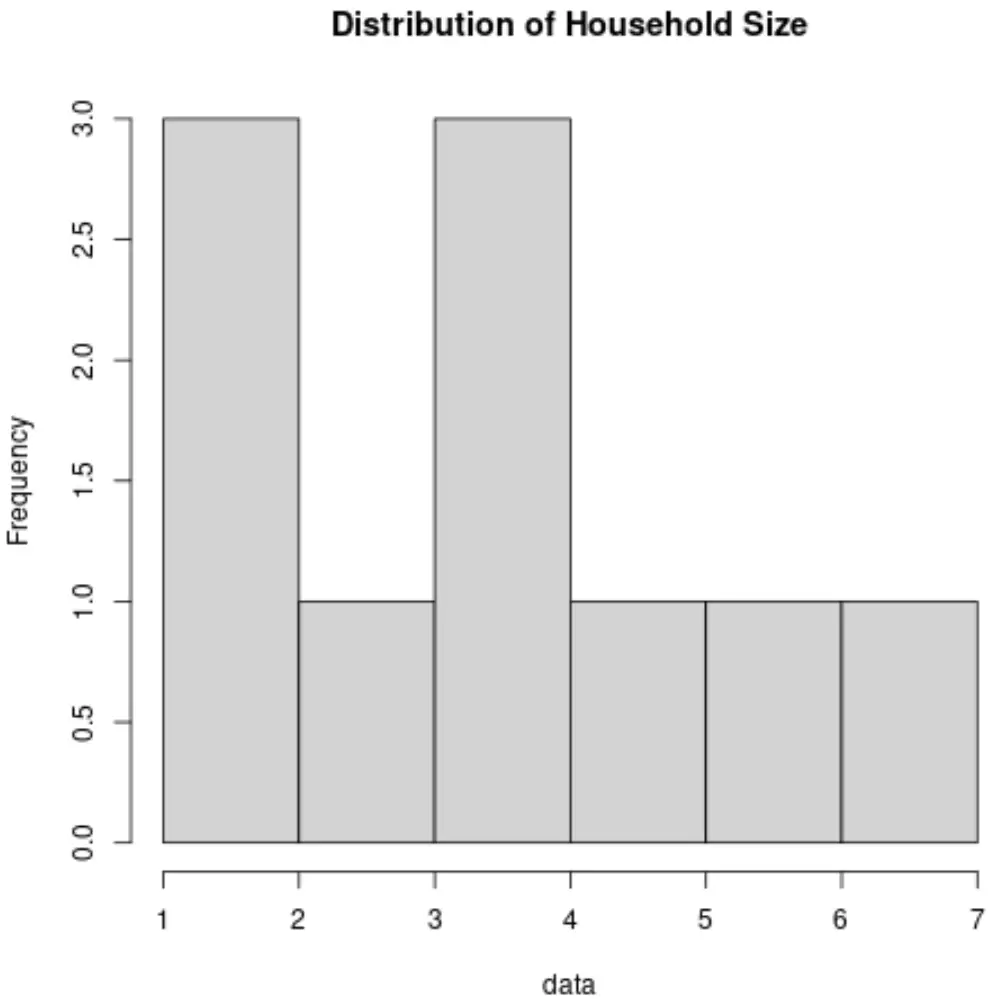
2. Histogramme

Un histogramme est un type de graphique qui utilise des barres verticales pour afficher les fréquences. Ce type de graphique est un moyen utile pour visualiser la distribution des valeurs dans un ensemble de données.

Voici à quoi ressemblerait un histogramme pour la variable Taille du ménage :

3. Courbe de densité

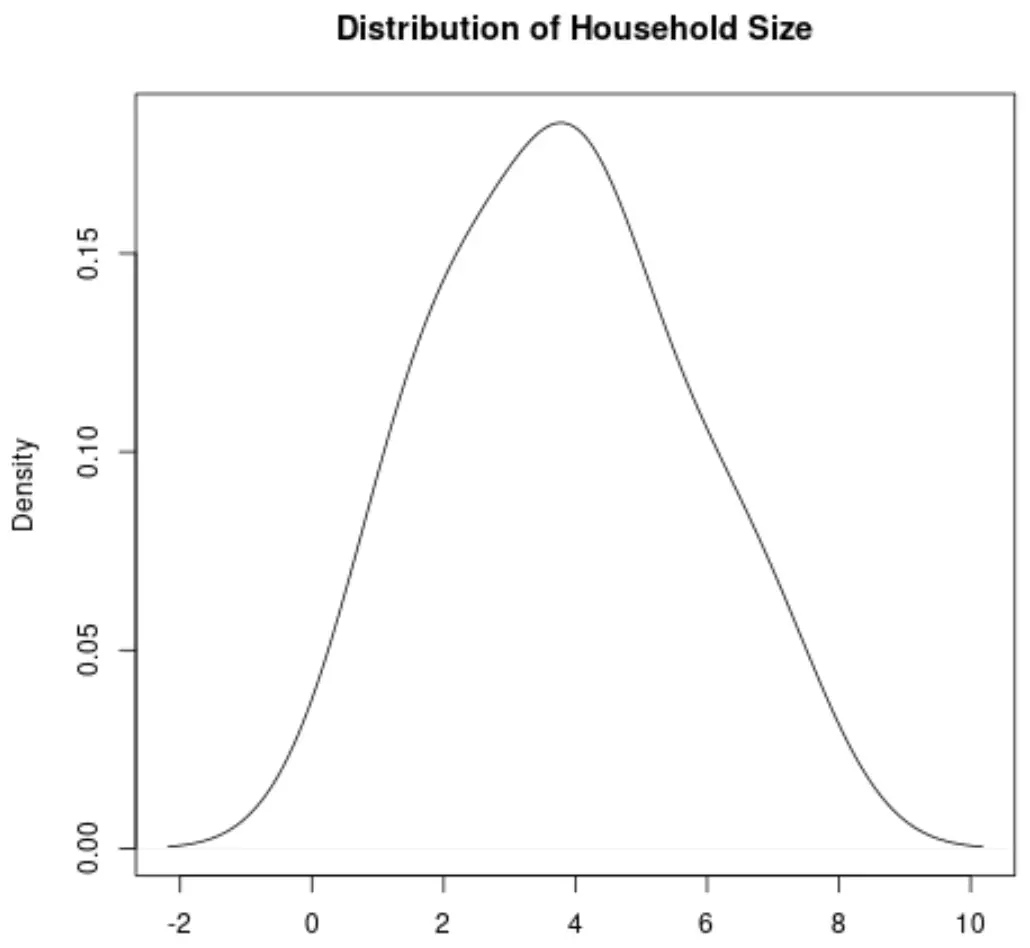
Une courbe de densité est une courbe sur un graphique qui représente la distribution des valeurs dans un ensemble de données.

Il est particulièrement utile pour visualiser la « forme » d’une distribution, notamment si une distribution présente ou non un ou plusieurs « pics » de valeurs fréquentes et si la distribution est asymétrique ou non vers la gauche ou la droite .

Voici à quoi ressemblerait une courbe de densité pour la variable Taille du ménage :

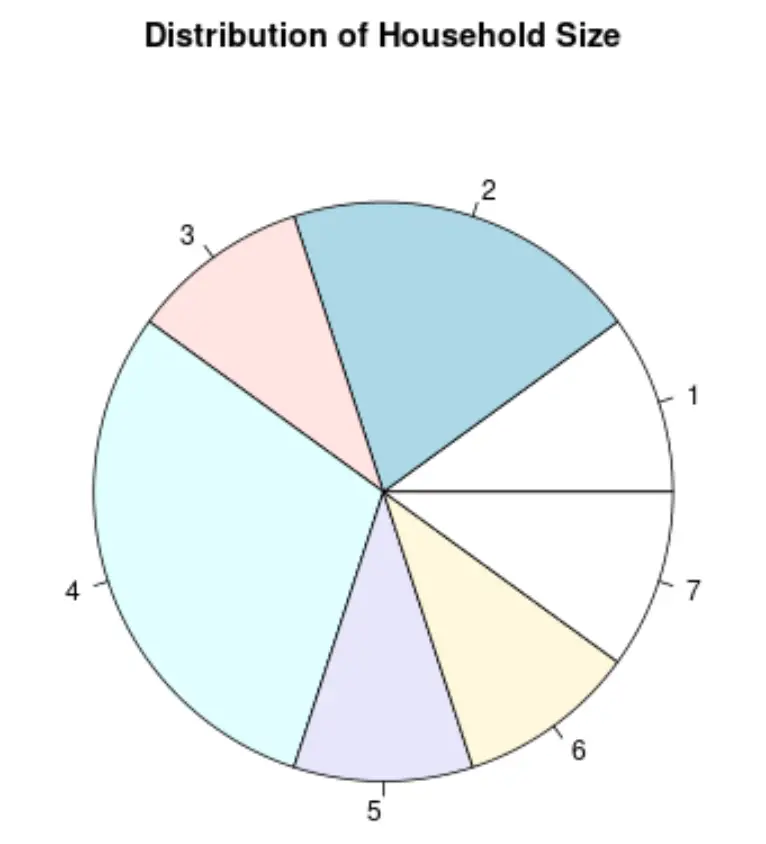
4. Graphique circulaire

Un diagramme circulaire est un type de graphique en forme de cercle et utilise des tranches pour représenter les proportions d’un tout.

Voici à quoi ressemblerait un diagramme circulaire pour la variable Taille du ménage :

Selon le type de données, l’un de ces graphiques peut être plus utile que les autres pour visualiser la distribution des valeurs.