Que sont les résidus dans les statistiques ?

Un résidu est la différence entre une valeur observée et une valeur prédite dans l’analyse de régression .

Il est calculé comme suit :

Résiduel = Valeur observée – Valeur prédite

Rappelons que le but de la régression linéaire est de quantifier la relation entre une ou plusieurs variables prédictives et une variable de réponse . Pour ce faire, la régression linéaire trouve la droite qui « correspond » le mieux aux données, appelée droite de régression des moindres carrés .

Cette droite produit une prédiction pour chaque observation de l’ensemble de données, mais il est peu probable que la prédiction faite par la droite de régression corresponde exactement à la valeur observée.

La différence entre la prédiction et la valeur observée est le résidu. Si nous traçons les valeurs observées et superposons la droite de régression ajustée, les résidus pour chaque observation seraient la distance verticale entre l’observation et la droite de régression :

Une observation a un résidu positif si sa valeur est supérieure à la valeur prédite faite par la droite de régression.

A l’inverse, une observation a un résidu négatif si sa valeur est inférieure à la valeur prédite faite par la droite de régression.

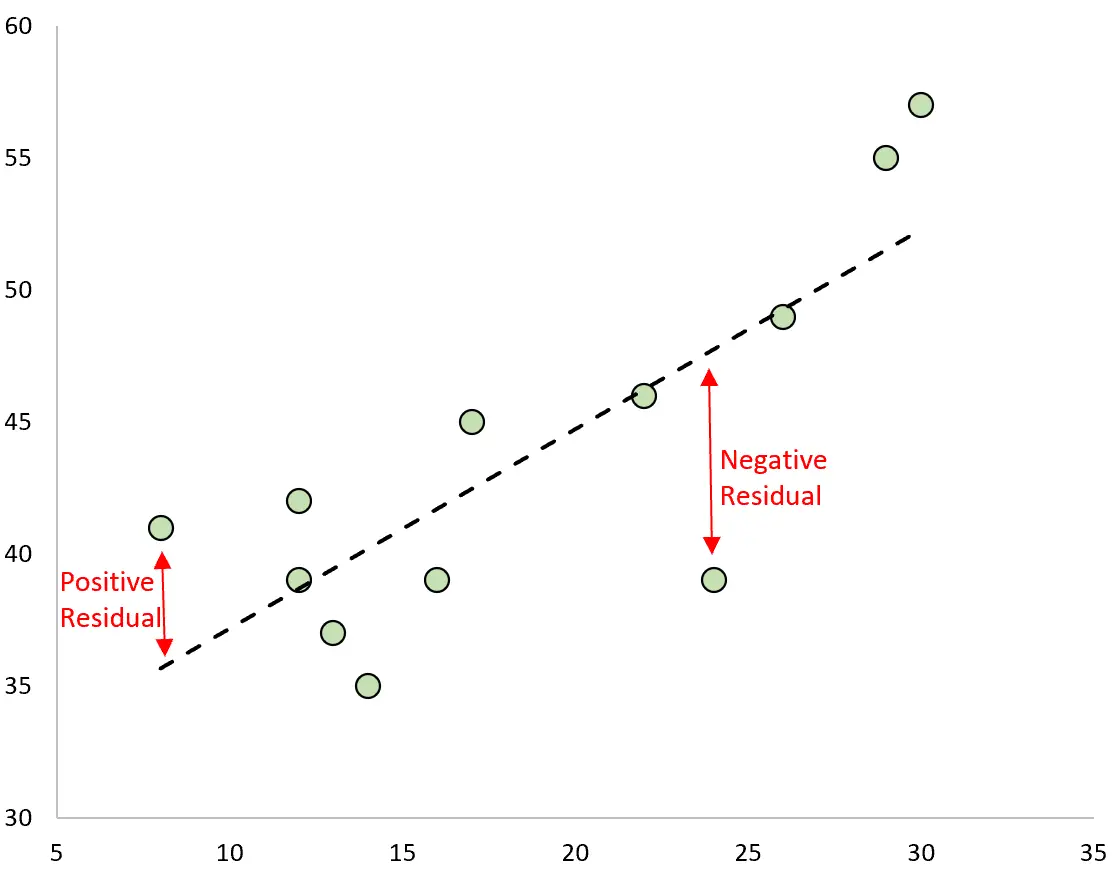
Certaines observations auront des résidus positifs tandis que d’autres auront des résidus négatifs, mais tous les résidus totaliseront zéro .

Exemple de calcul des résidus

Supposons que nous ayons l’ensemble de données suivant avec 12 observations au total :

Si nous utilisons un logiciel statistique (comme R , Excel , Python , Stata , etc.) pour ajuster une droite de régression linéaire à cet ensemble de données, nous constaterons que la droite la mieux ajustée s’avère être :

y = 29,63 + 0,7553x

En utilisant cette ligne, nous pouvons calculer la valeur prédite pour chaque valeur Y en fonction de la valeur de X. Par exemple, la valeur prédite de la première observation serait :

y = 29,63 + 0,7553*(8) = 35,67

Nous pouvons alors calculer le résidu pour cette observation comme suit :

Résiduel = Valeur observée – Valeur prédite = 41 – 35,67 = 5,33

Nous pouvons répéter ce processus pour trouver le résidu pour chaque observation :

Si nous créons un nuage de points pour visualiser les observations avec la droite de régression ajustée, nous verrons que certaines des observations se situent au-dessus de la ligne tandis que d’autres se situent en dessous de la ligne :

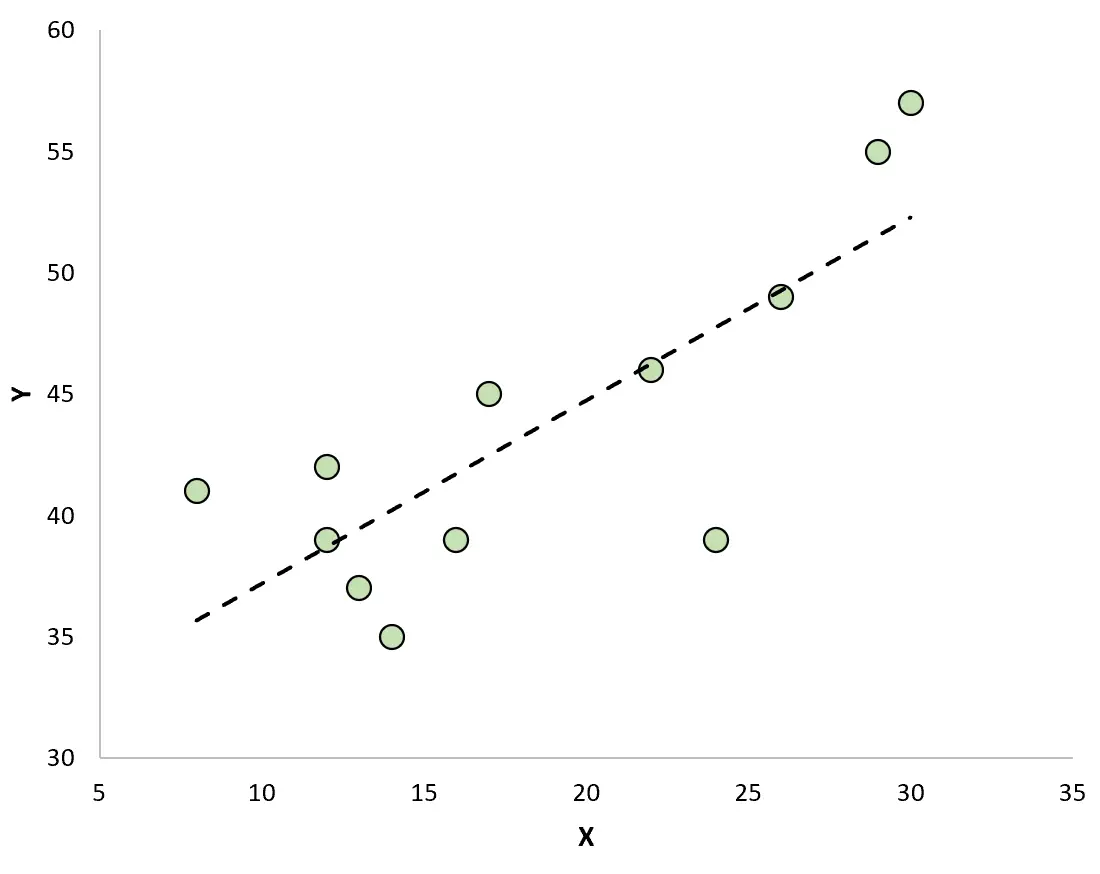
Propriétés des résidus

Les résidus ont les propriétés suivantes :

• Chaque observation dans un ensemble de données a un résidu correspondant. Ainsi, si un ensemble de données contient 100 observations au total, le modèle produira 100 valeurs prédites, ce qui donnera 100 résidus au total.
• La somme de tous les résidus est égale à zéro.
• La valeur moyenne des résidus est nulle.

Comment les résidus sont-ils utilisés en pratique ?

En pratique, les résidus sont utilisés pour trois raisons différentes en régression :

1. Évaluez l’adéquation du modèle.

Une fois que nous avons produit une droite de régression ajustée, nous pouvons calculer la somme des carrés des résidus (RSS) , qui est la somme de tous les carrés des résidus. Plus le RSS est faible, mieux le modèle de régression s’adapte aux données.

2. Vérifiez l’hypothèse de normalité.

L’une des hypothèses clés de la régression linéaire est que les résidus sont normalement distribués.

Pour vérifier cette hypothèse, nous pouvons créer un tracé QQ, qui est un type de tracé que nous pouvons utiliser pour déterminer si les résidus d’un modèle suivent ou non une distribution normale.

Si les points sur le tracé forment à peu près une ligne diagonale droite, alors l’hypothèse de normalité est remplie.

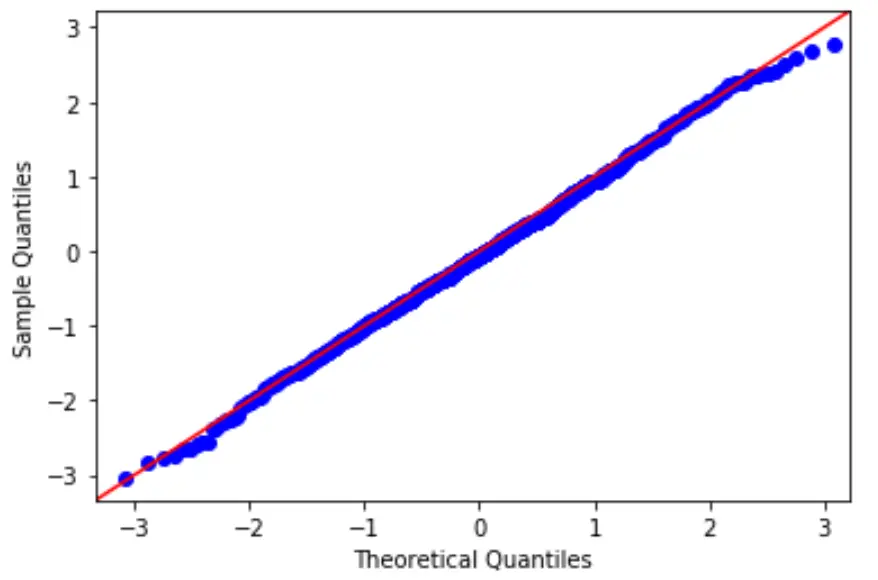
3. Vérifiez l’hypothèse d’homoscédasticité.

Une autre hypothèse clé de la régression linéaire est que les résidus ont une variance constante à chaque niveau de x. C’est ce qu’on appelle l’homoscédasticité. Lorsque ce n’est pas le cas, les résidus souffrent d’ hétéroscédasticité .

Pour vérifier si cette hypothèse est remplie, nous pouvons créer un tracé des résidus , qui est un nuage de points qui montre les résidus par rapport aux valeurs prédites du modèle.

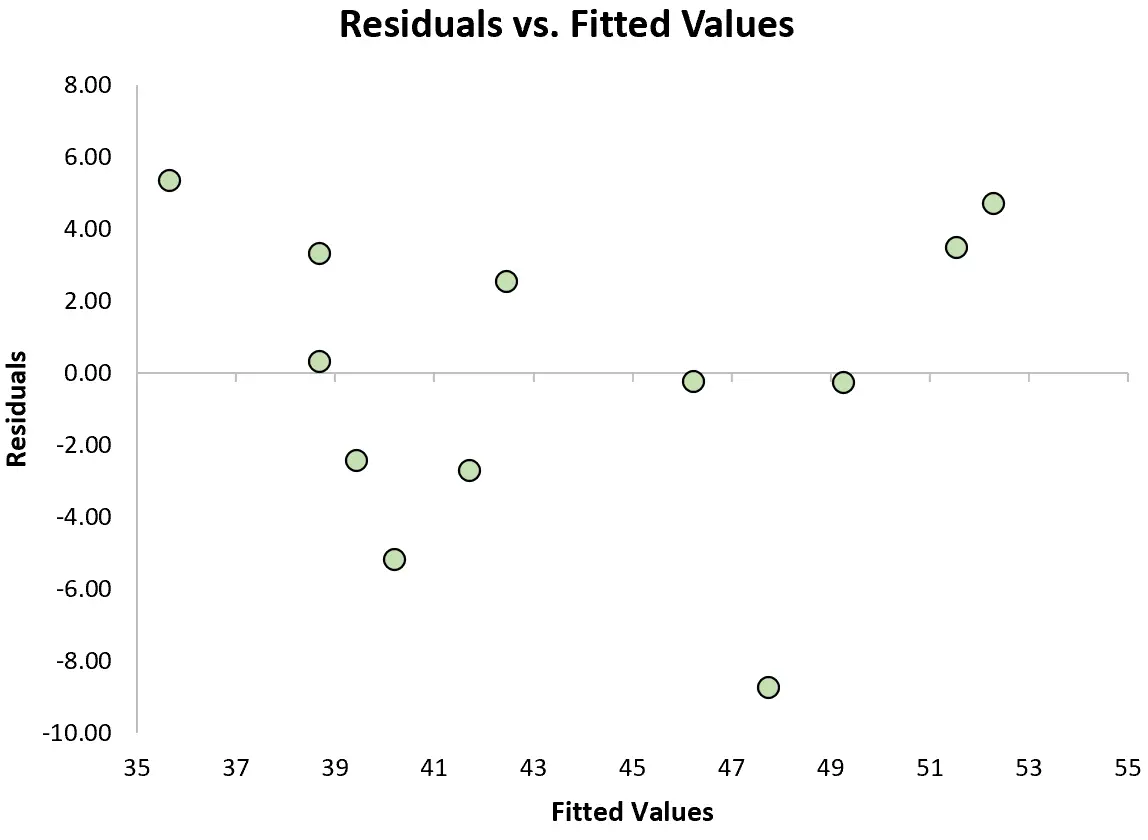
Si les résidus sont répartis à peu près uniformément autour de zéro dans le graphique sans tendance claire, alors nous disons généralement que l’hypothèse d’homoscédasticité est remplie.

Ressources additionnelles

Introduction à la régression linéaire simple
Introduction à la régression linéaire multiple
Les quatre hypothèses de la régression linéaire
Comment créer un tracé résiduel dans Excel