Splines de régression adaptative multivariée dans R
Les splines de régression adaptative multivariées (MARS) peuvent être utilisées pour modéliser des relations non linéaires entre un ensemble de variables prédictives et une variable de réponse .
Cette méthode fonctionne comme suit :
1. Divisez un ensemble de données en k morceaux.
2. Ajustez un modèle de régression à chaque pièce.
3. Utilisez la validation croisée k-fold pour choisir une valeur pour k .
Ce didacticiel fournit un exemple étape par étape de la façon d’adapter un modèle MARS à un ensemble de données dans R.
Étape 1 : Charger les packages nécessaires
Pour cet exemple, nous utiliserons l’ensemble de données Wage de l’ ISLR. package, qui contient les salaires annuels de 3 000 personnes ainsi qu’une variété de variables prédictives telles que l’âge, l’éducation, la race, etc.
Avant d’adapter un modèle MARS aux données, nous allons charger les packages nécessaires :
library(ISLR) #contains Wage dataset library(dplyr) #data wrangling library(ggplot2) #plotting library(earth) #fitting MARS models library(caret) #tuning model parameters
Étape 2 : Afficher les données
Ensuite, nous afficherons les six premières lignes de l’ensemble de données avec lequel nous travaillons :
#view first six rows of data
head(Wage)
year age maritl race education region
231655 2006 18 1. Never Married 1. White 1. < HS Grad 2. Middle Atlantic
86582 2004 24 1. Never Married 1. White 4. College Grad 2. Middle Atlantic
161300 2003 45 2. Married 1. White 3. Some College 2. Middle Atlantic
155159 2003 43 2. Married 3. Asian 4. College Grad 2. Middle Atlantic
11443 2005 50 4. Divorced 1. White 2. HS Grad 2. Middle Atlantic
376662 2008 54 2. Married 1. White 4. College Grad 2. Middle Atlantic
jobclass health health_ins logwage wage
231655 1. Industrial 1. <=Good 2. No 4.318063 75.04315
86582 2. Information 2. >=Very Good 2. No 4.255273 70.47602
161300 1. Industrial 1. <=Good 1. Yes 4.875061 130.98218
155159 2. Information 2. >=Very Good 1. Yes 5.041393 154.68529
11443 2. Information 1. <=Good 1. Yes 4.318063 75.04315
376662 2. Information 2. >=Very Good 1. Yes 4.845098 127.11574
Étape 3 : Créer et optimiser le modèle MARS
Ensuite, nous allons créer le modèle MARS pour cet ensemble de données et effectuer une validation croisée k fois pour déterminer quel modèle produit le RMSE (erreur quadratique moyenne) de test le plus bas.
#create a tuning grid
hyper_grid <- expand.grid(degree = 1:3,
nprune = seq(2, 50, length.out = 10) %>%
floor())
#make this example reproducible
set.seed(1)
#fit MARS model using k-fold cross-validation
cv_mars <- train(
x = subset(Wage, select = -c(wage, logwage)),
y = Wage$wage,
method = "earth",
metric = "RMSE",
trControl = trainControl(method = "cv", number = 10),
tuneGrid = hyper_grid)
#display model with lowest test RMSE
cv_mars$results %>%
filter(nprune==cv_mars$bestTune$nprune, degree =cv_mars$bestTune$degree)
degree nprune RMSE Rsquared MAE RMSESD RsquaredSD MAESD
1 12 33.8164 0.3431804 22.97108 2.240394 0.03064269 1.4554
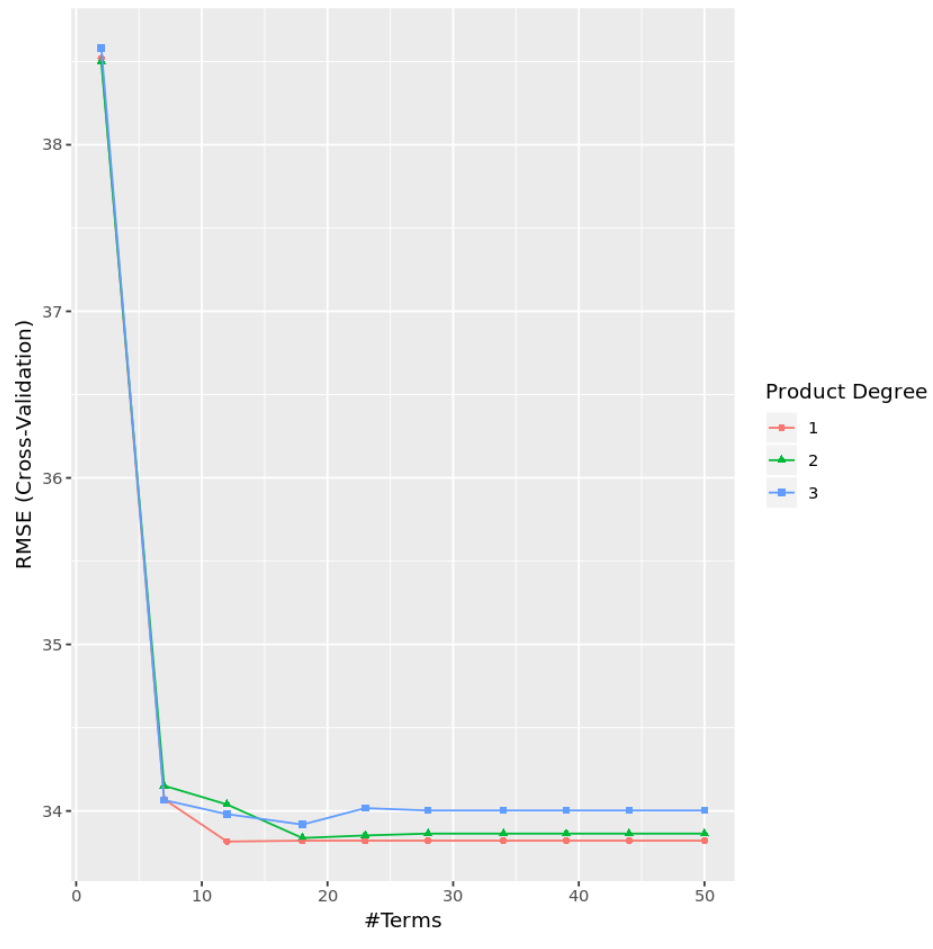
À partir des résultats, nous pouvons voir que le modèle qui a produit le MSE de test le plus bas était un modèle avec uniquement des effets de premier ordre (c’est-à-dire aucun terme d’interaction) et 12 termes. Ce modèle a produit une erreur quadratique moyenne (RMSE) de 33,8164 .
Remarque : Nous avons utilisé method= »earth » pour spécifier un modèle MARS. Vous pouvez trouver la documentation de cette méthode ici .
Nous pouvons également créer un graphique pour visualiser le test RMSE en fonction du degré et du nombre de termes :
#display test RMSE by terms and degree
ggplot(cv_mars)
En pratique, nous adapterions un modèle MARS avec plusieurs autres types de modèles comme :
- La régression linéaire multiple
- Régression polynomiale
- Régression de crête
- Régression au lasso
- Régression des composantes principales
- Moindres carrés partiels
Nous comparerions ensuite chaque modèle pour déterminer lequel conduit à l’erreur de test la plus faible et choisirions ce modèle comme étant le modèle optimal à utiliser.
Le code R complet utilisé dans cet exemple peut être trouvé ici .
