Comment effectuer un test de Kruskal-Wallis dans SPSS

Un test de Kruskal-Wallis est utilisé pour déterminer s’il existe ou non une différence statistiquement significative entre les médianes de trois groupes indépendants ou plus. Elle est considérée comme l’équivalent non paramétrique de l’ ANOVA unidirectionnelle .

Ce didacticiel explique comment effectuer un test de Kruskal-Wallis dans SPSS.

Exemple : test de Kruskal-Wallis dans SPSS

Un chercheur veut savoir si trois médicaments ont des effets différents sur la douleur au genou. Il recrute donc 30 personnes qui ressentent toutes une douleur au genou similaire et les divise au hasard en trois groupes pour recevoir soit le médicament 1, le médicament 2 ou le médicament 3.

Après un mois de prise du médicament, le chercheur demande à chaque individu d’évaluer sa douleur au genou sur une échelle de 1 à 100, 100 indiquant la douleur la plus intense. Les notes des 30 personnes sont présentées ci-dessous :

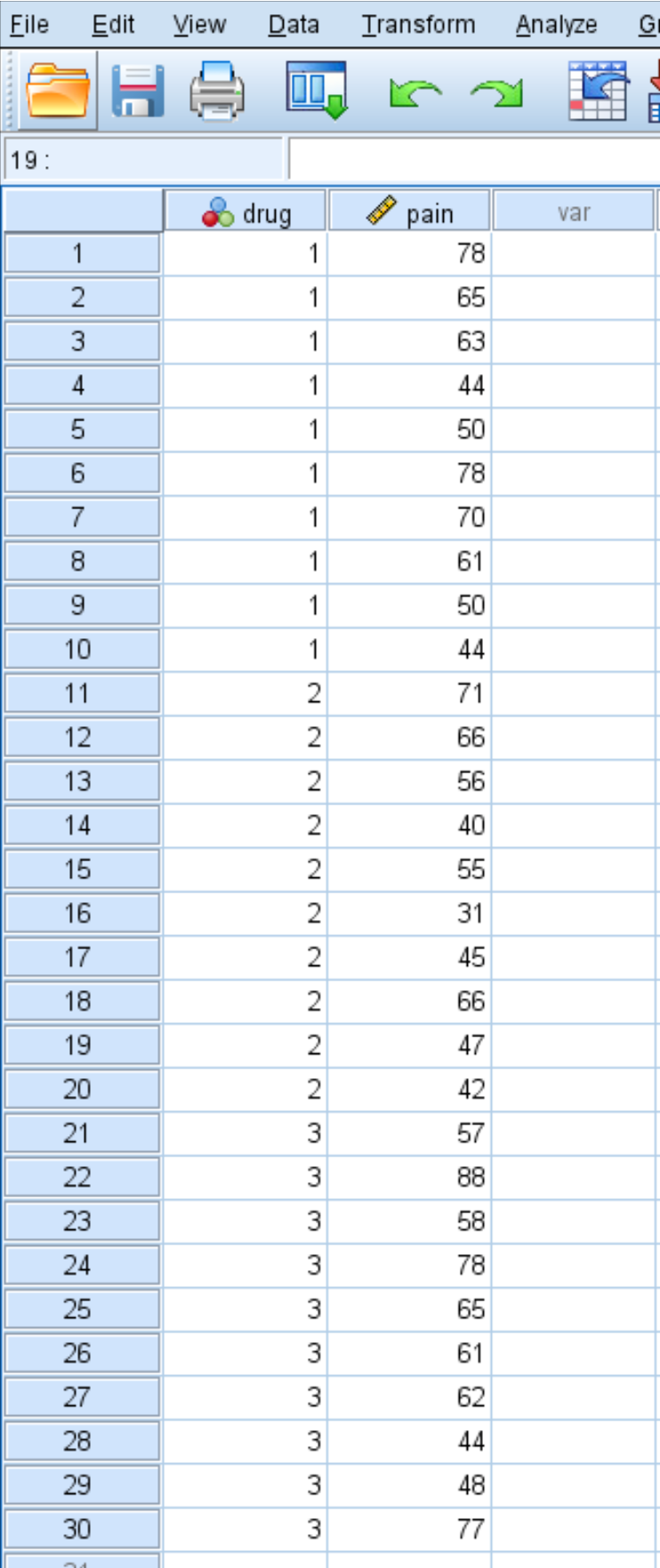
Suivez les étapes suivantes pour effectuer un test de Kruskal-Wallis afin de déterminer s’il existe ou non une différence entre les niveaux de douleur au genou signalés entre les trois groupes :

Étape 1 : effectuez un test de Kruskal-Wallis.

Cliquez sur l’onglet Analyser , puis sur Tests non paramétriques , puis sur Legacy Dialogs , puis sur K Independent Samples :

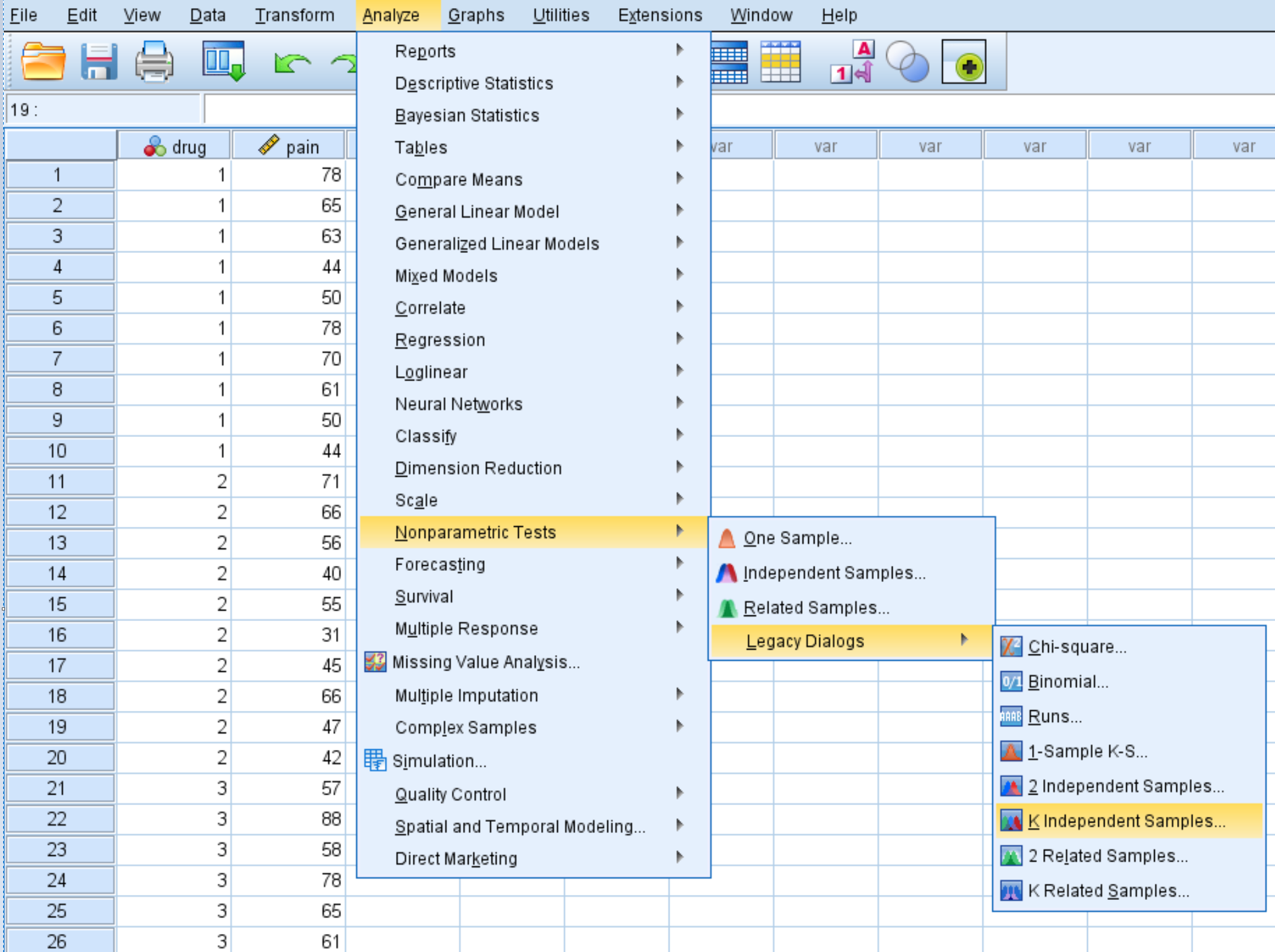
Dans la fenêtre qui apparaît, faites glisser la variable douleur dans la case intitulée Liste des variables de test et médicament dans la case intitulée Variable de regroupement. Cliquez ensuite sur Définir la plage et définissez la valeur minimale sur 1 et la valeur maximale sur 3. Cliquez ensuite sur Continuer . Assurez-vous que la case à côté de Kruskal-Wallis H est cochée, puis cliquez sur OK .

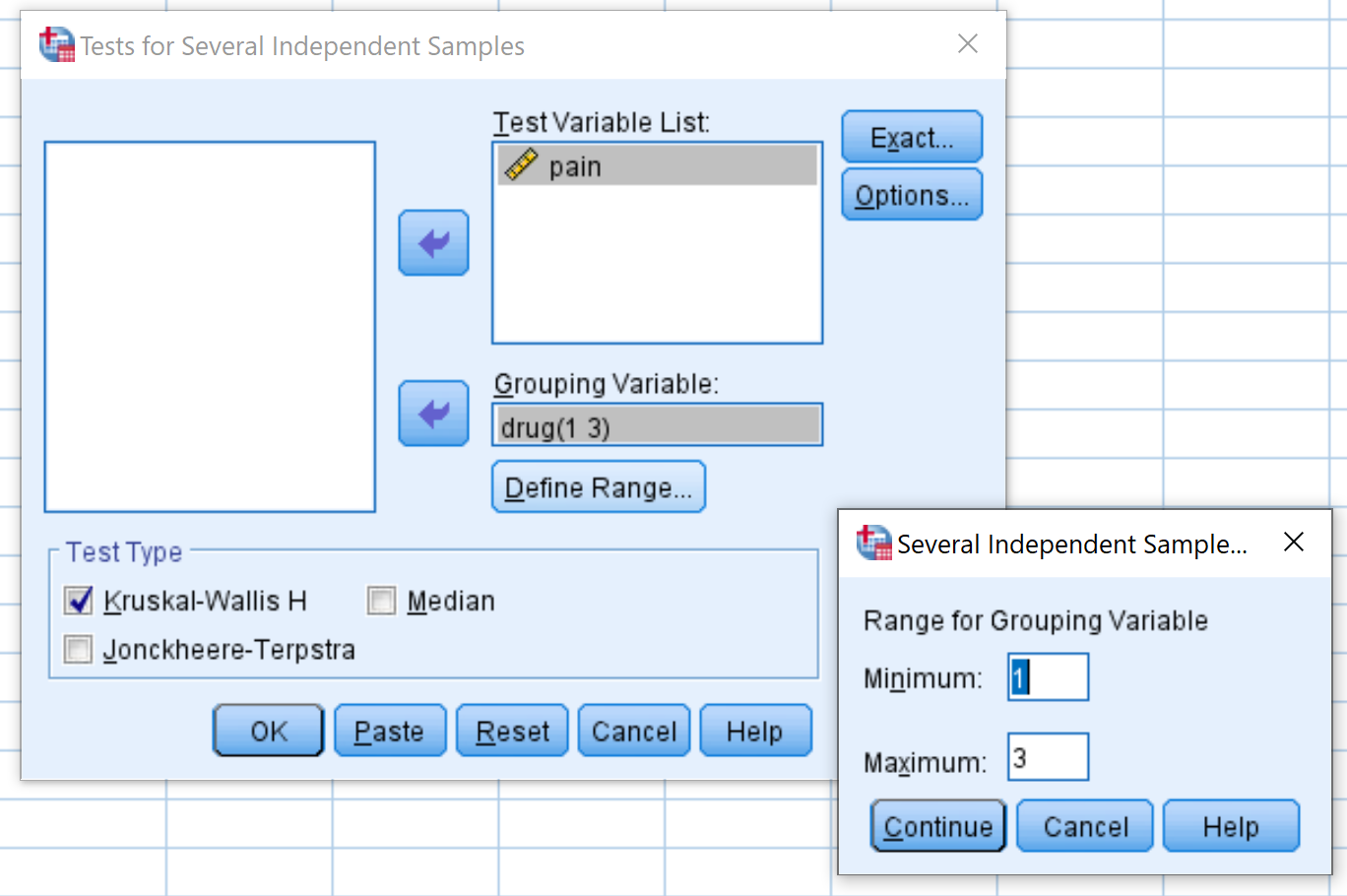
Étape 2 : Interprétez les résultats.

Une fois que vous cliquez sur OK , les résultats du test de Kruskal-Wallis apparaîtront :

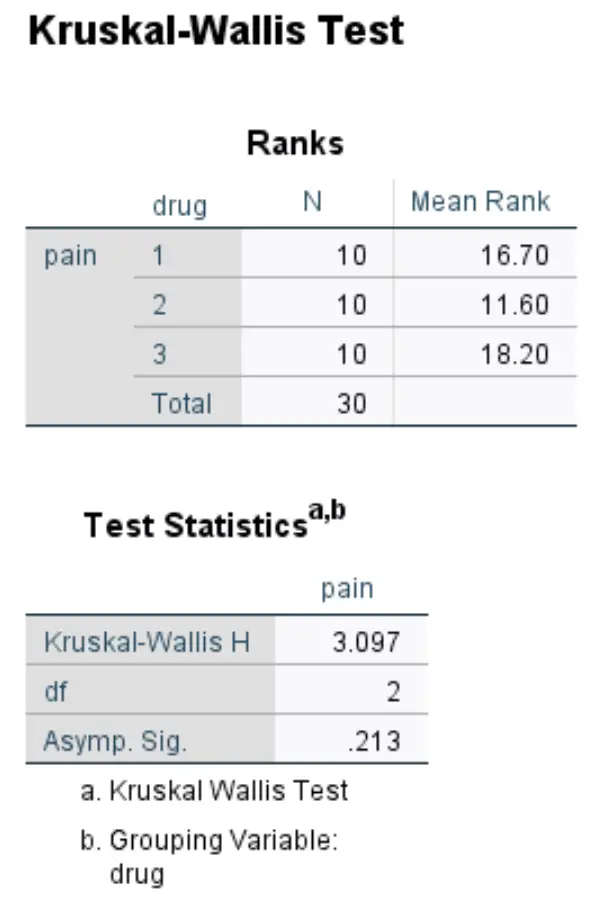
Le deuxième tableau de la sortie affiche les résultats du test :

• Kruskal-Wallis H : Il s’agit de la statistique du test X ² .
• df : Il s’agit des degrés de liberté, calculés comme #groups-1 = 3-1 = 2.
• Asymp. Sig : Il s’agit de la valeur p associée à une statistique de test X ² de 3,097 avec 2 degrés de liberté. Cela peut également être trouvé en utilisant le calculateur du score du chi carré vers la valeur P.

Puisque la valeur p (0,213) n’est pas inférieure à 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle. Nous ne disposons pas de preuves suffisantes pour affirmer qu’il existe une différence statistiquement significative entre les évaluations de la douleur au genou entre ces trois groupes.