Comment effectuer le test exact de Fisher dans SPSS
Le test exact de Fisher est utilisé pour déterminer s’il existe ou non une association significative entre deux variables catégorielles.
Il est généralement utilisé comme alternative au test d’indépendance du chi carré lorsqu’un ou plusieurs comptes de cellules dans un tableau 2 × 2 sont inférieurs à 5.
Ce didacticiel explique comment effectuer le test exact de Fisher dans SPSS.
Exemple : test exact de Fisher dans SPSS
Supposons que nous voulions savoir si le sexe est associé ou non à la préférence pour un parti politique dans un collège particulier. Pour explorer cela, nous interrogeons au hasard 25 étudiants sur le campus. Le nombre d’étudiants démocrates ou républicains, en fonction de leur sexe, est indiqué dans le tableau ci-dessous :
| Démocrate | Républicain | |
|---|---|---|
| Femelle | 8 | 4 |
| Mâle | 4 | 9 |
Pour déterminer s’il existe une association statistiquement significative entre le sexe et la préférence pour un parti politique, nous pouvons utiliser les étapes suivantes pour effectuer le test exact de Fisher dans SPSS :
Étape 1 : Saisissez les données.
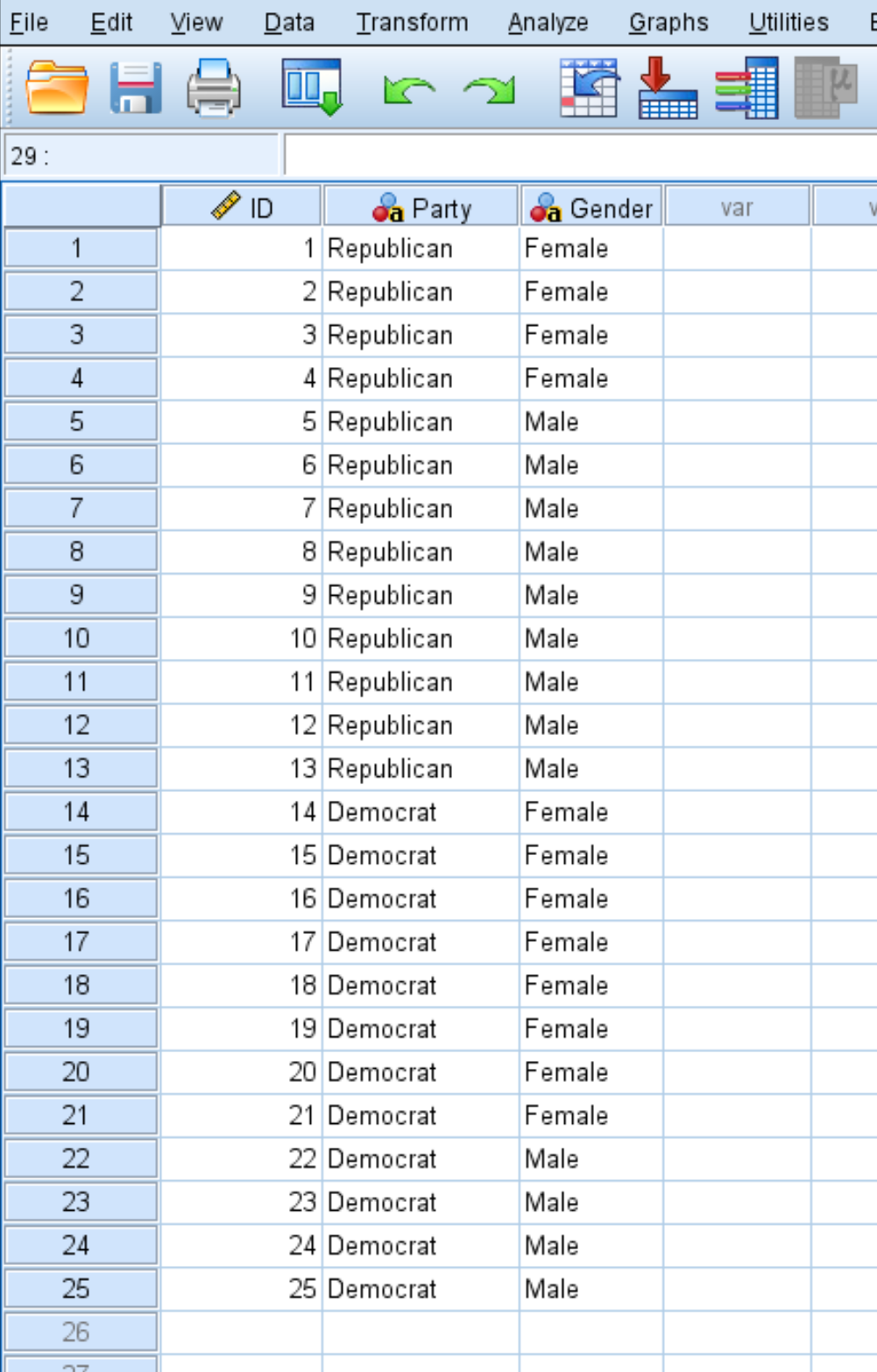
Tout d’abord, saisissez les données comme indiqué ci-dessous :
Chaque ligne affiche la pièce d’identité d’un individu, sa préférence en matière de parti politique et son sexe.
Étape 2 : Effectuez le test exact de Fisher.
Cliquez sur l’onglet Analyser , puis sur Statistiques descriptives , puis sur Tableaux croisés :
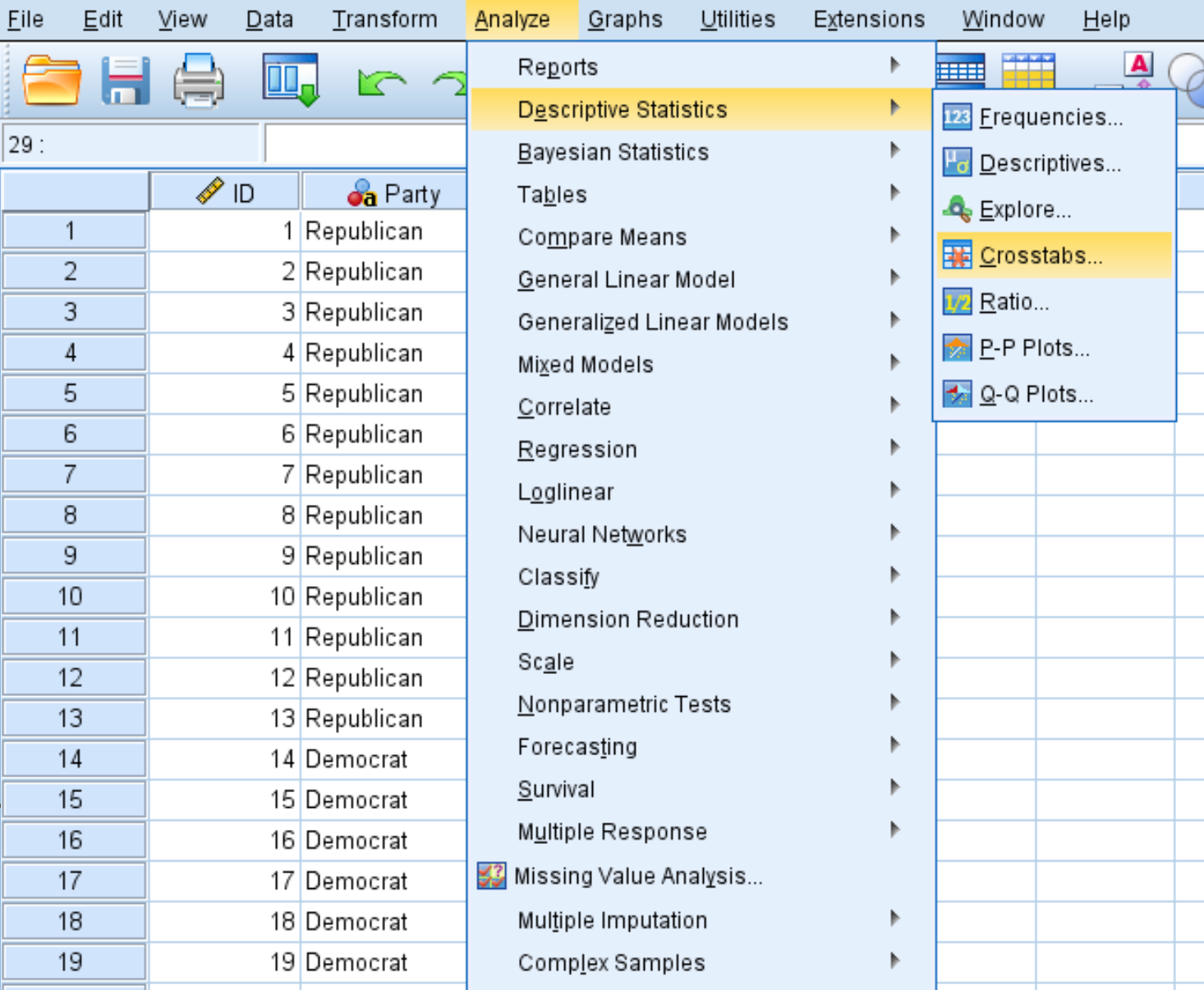
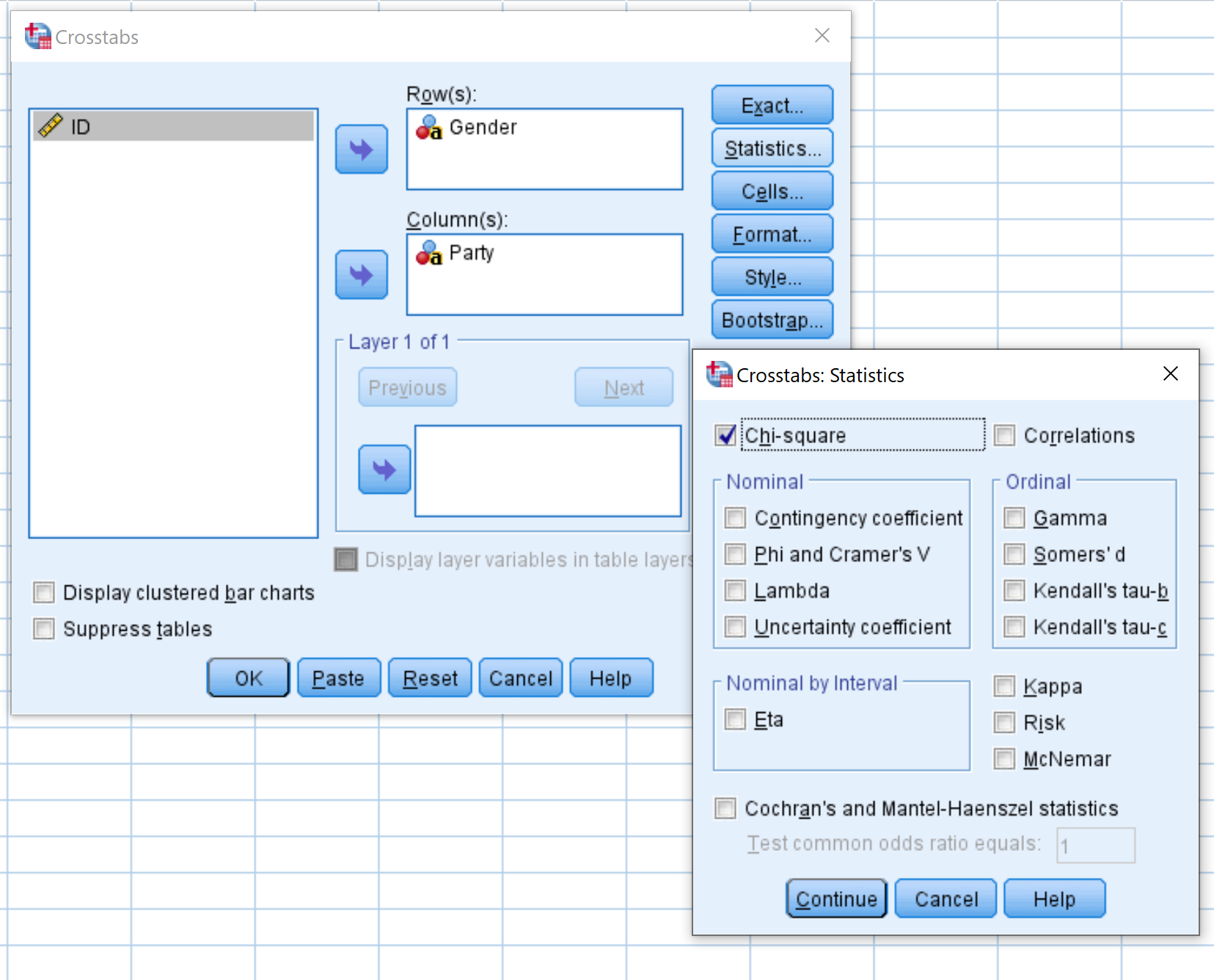
Faites glisser la variable Sexe dans la zone intitulée Lignes et la variable Partie dans la zone intitulée Colonnes. Cliquez ensuite sur le bouton intitulé Statistiques et assurez-vous que la case à côté de Chi carré est cochée. Cliquez ensuite sur Continuer .
Ensuite, cliquez sur le bouton intitulé Exact et assurez-vous que la case à côté d’ Exact est cochée. Cliquez ensuite sur Continuer .
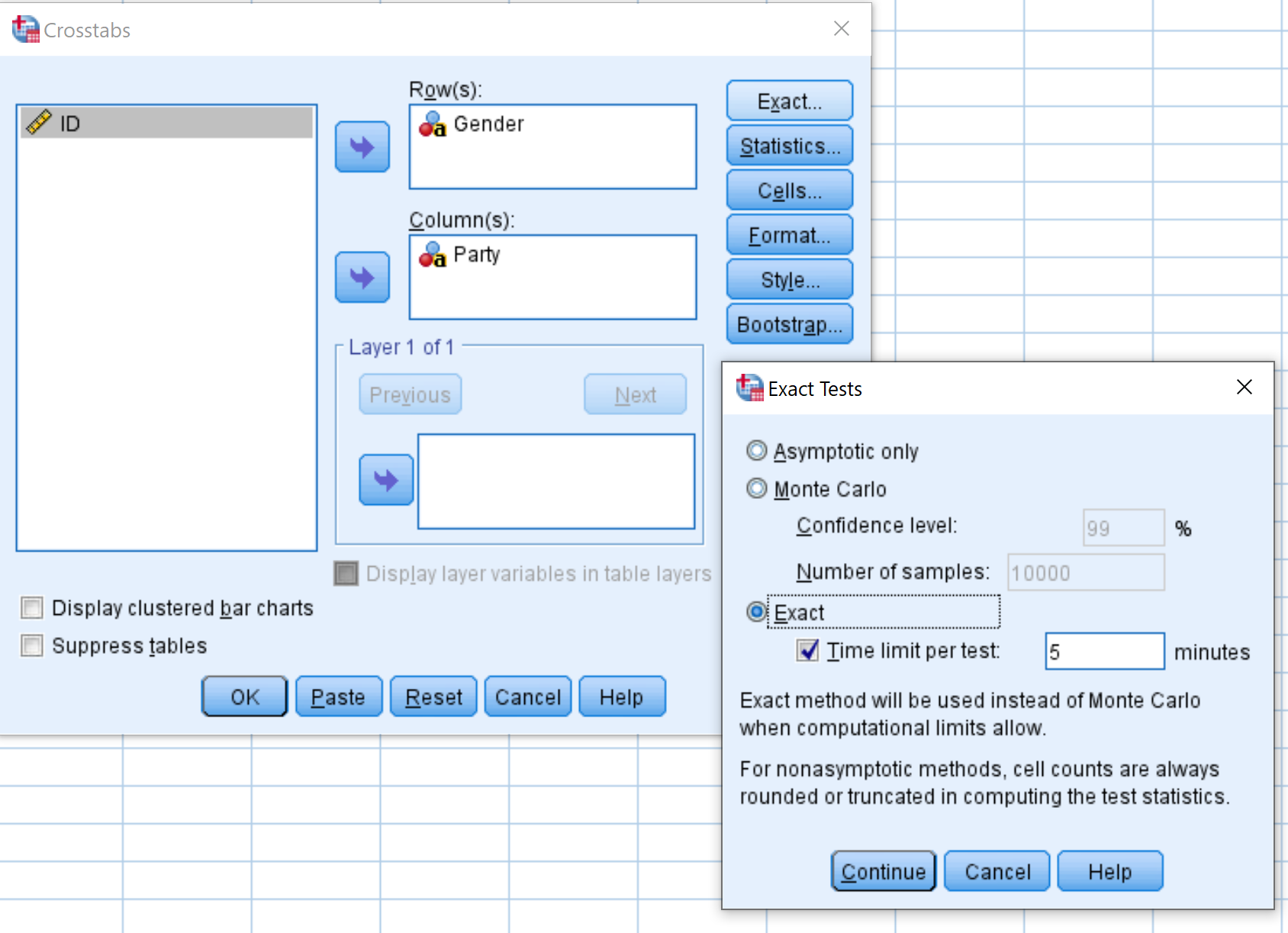
Enfin, cliquez sur OK pour effectuer le test exact de Fisher.
Étape 3 : Interprétez les résultats.
Une fois que vous avez cliqué sur OK , les résultats du test exact de Fisher s’afficheront :
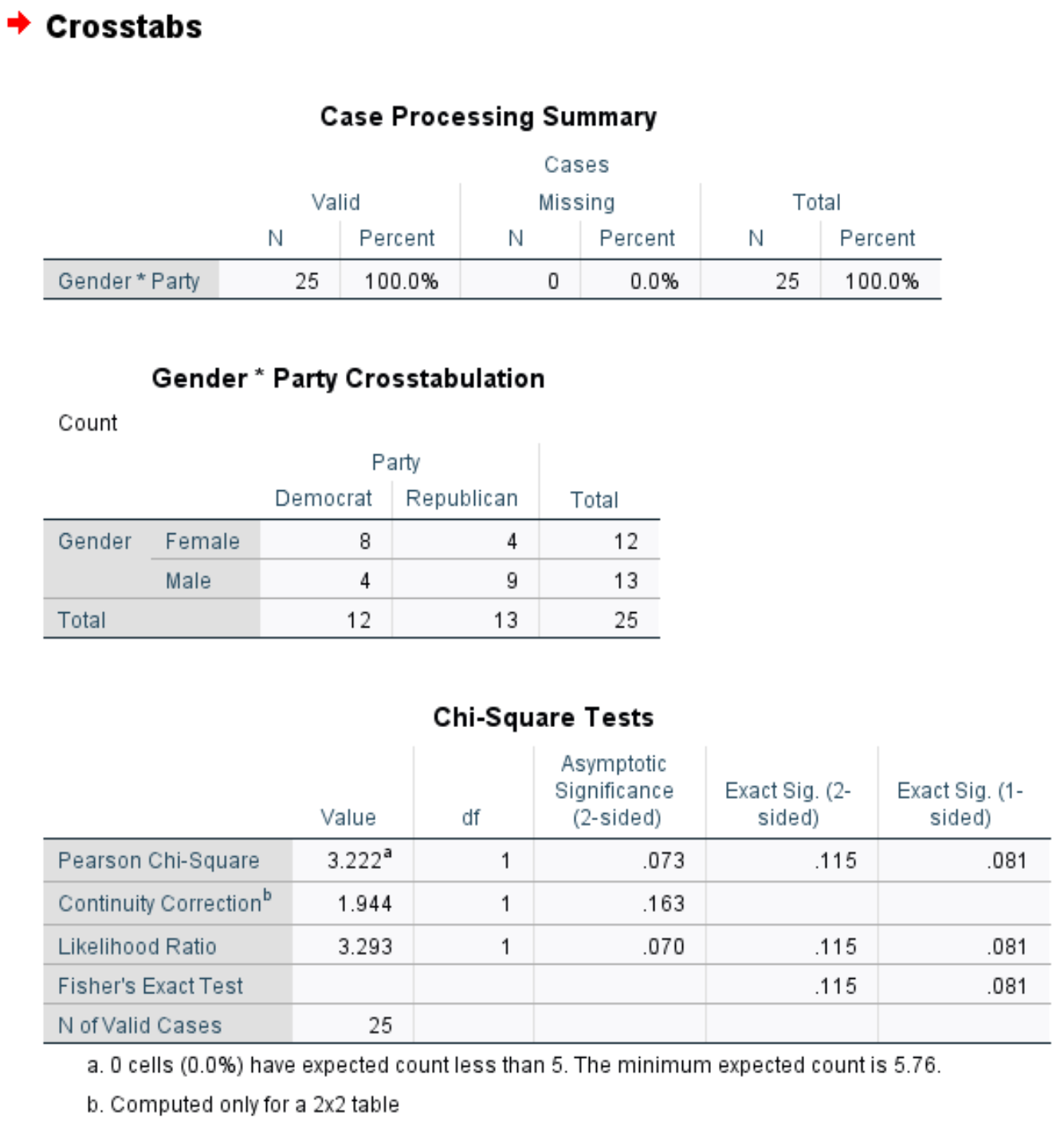
Le premier tableau affiche le nombre de cas manquants dans l’ensemble de données. Nous pouvons voir qu’il y a 0 cas manquant dans cet exemple.
Le deuxième tableau présente un tableau croisé du nombre total d’individus par sexe et préférence de parti politique.
Le troisième tableau montre les résultats du test exact de Fisher. Nous pouvons voir les deux valeurs p suivantes pour le test :
- Valeur p bilatérale : 0,115
- Valeur p unilatérale : 0,081
L’hypothèse nulle du test exact de Fisher est que les deux variables sont indépendantes. Dans ce cas, notre hypothèse nulle est que le sexe et la préférence pour le parti politique sont indépendants, ce qui est un test bilatéral, nous utiliserions donc la valeur p bilatérale de 0,115.
Puisque cette valeur p n’est pas inférieure à 0,05, nous ne rejetons pas l’hypothèse nulle. Nous ne disposons donc pas de preuves suffisantes pour affirmer qu’il existe une association significative entre le sexe et la préférence en matière de parti politique.
