Matrice de covariance

Cet article explique ce qu’est la matrice de covariance et quelle est sa formule. Vous découvrirez comment réaliser la matrice de covariance avec un exemple concret et les propriétés des matrices de covariance.

Qu’est-ce que la matrice de covariance ?

La matrice de covariance est une matrice carrée dont les éléments sont les variances et covariances des variables étudiées. Ainsi, les éléments de la diagonale principale de la matrice de covariance sont la variance de chaque variable, et les éléments restants sont les covariances entre les variables.

En statistique, la matrice de covariance est utilisée pour analyser la relation entre deux ou plusieurs variables aléatoires. La matrice de covariance est très utile car elle permet d’interpréter rapidement la corrélation entre de nombreuses variables, puisque vous pouvez voir les valeurs de toutes les covariances des variables en même temps.

Le symbole de la matrice de covariance est la lettre grecque majuscule sigma (Σ).

Comment calculer la matrice de covariance

Pour calculer la matrice de covariance de plusieurs variables statistiques, les étapes suivantes doivent être réalisées :

1. Calculez les variances de toutes les variables.
2. Calculez la covariance de chaque paire de variables.
3. Former la matrice de covariance :
• La variance de la variable i doit être placée sur la diagonale principale de la matrice, plus précisément en position i,i .
• La covariance entre les variables i et j doit être mise en position i,j de la matrice.

La formule de la matrice de covariance est donc la suivante :

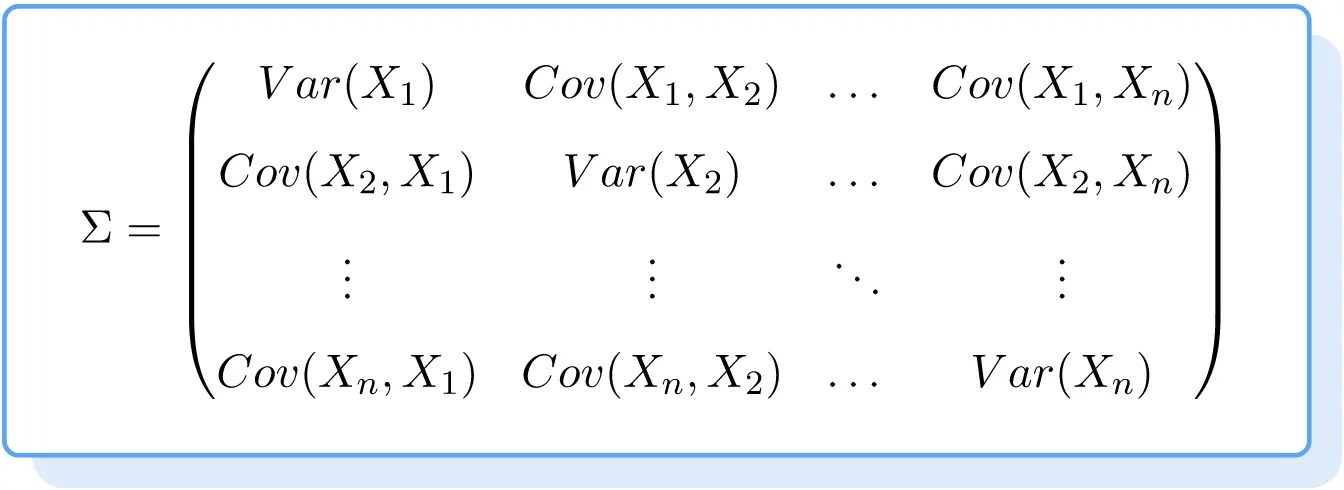
Exemple de matrice de covariance

Après avoir vu la définition de la matrice de covariance, vous trouverez ci-dessous un exercice étape par étape afin que vous puissiez voir comment ce type de matrice est réalisé.

Calcule la matrice de covariance des variables X, Y et Z, dont les valeurs sont :

• X : 4, 7, 12, 5, 7
• Et : 9, 15, 19, 6, 8
• Z : 7, 2, 4, 6, 3

La première chose que nous devons faire est de déterminer les variances de toutes les variables :

Deuxièmement, nous trouvons la covariance entre chaque paire de variables :

Et une fois que l’on a calculé toutes les variances et covariances, il ne reste plus qu’à faire la matrice de covariance. Pour ce faire, on met les valeurs de variance sur la diagonale principale de la matrice et les valeurs de covariance dans leur position correspondante :

Comme vous pouvez le constater, en représentant les variances et covariances dans une matrice, il est très facile d’interpréter les variables. La variable avec la plus grande dispersion est Y (23.44), par contre les variables X et Y ont une relation directe, tandis que les variables X et Z (et par conséquent Y et Z) ont une relation inverse.

Notez que la matrice de covariance est toujours symétrique, puisque la covariance entre deux variables ne dépend pas de l’ordre des variables. Par exemple,

est égal à

De plus, la matrice de covariance sera toujours une matrice carrée et sa dimension sera égale au nombre de variables. Dans ce cas, nous avions trois variables et c’est pourquoi c’est une matrice 3×3, mais si nous n’avions que deux variables, la matrice de covariance aurait été 2×2.

Propriétés de la matrice de covariance

La matrice de covariance présente les caractéristiques suivantes :

• La matrice de covariance est une matrice carrée de l’ordre du nombre de variables.
• La matrice de covariance est symétrique, ce qui signifie que la diagonale principale de la matrice est un axe de symétrie.
• La matrice de covariance est toujours semi-définie positive.
• Le déterminant de la matrice de covariance est égal ou supérieur à zéro.