Comment effectuer une analyse bivariée dans R (avec exemples)
Le terme analyse bivariée fait référence à l’analyse de deux variables. Vous pouvez vous en souvenir car le préfixe « bi » signifie « deux ».
Le but de l’analyse bivariée est de comprendre la relation entre deux variables
Il existe trois manières courantes d’effectuer une analyse bivariée :
1. Nuages de points
2. Coefficients de corrélation
3. Régression linéaire simple
L’exemple suivant montre comment effectuer chacun de ces types d’analyse bivariée à l’aide de l’ensemble de données suivant qui contient des informations sur deux variables : (1) Heures passées à étudier et (2) Résultats d’examen obtenus par 20 étudiants différents :
#create data frame df <- data.frame(hours=c(1, 1, 1, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 5, 5, 6, 6, 6, 7, 8), score=c(75, 66, 68, 74, 78, 72, 85, 82, 90, 82, 80, 88, 85, 90, 92, 94, 94, 88, 91, 96)) #view first six rows of data frame head(df) hours score 1 1 75 2 1 66 3 1 68 4 2 74 5 2 78 6 2 72
1. Nuages de points
Nous pouvons utiliser la syntaxe suivante pour créer un nuage de points des heures étudiées par rapport à la note de l’examen dans R :
#create scatterplot of hours studied vs. exam score plot(df$hours, df$score, pch=16, col='steelblue', main='Hours Studied vs. Exam Score', xlab='Hours Studied', ylab='Exam Score')
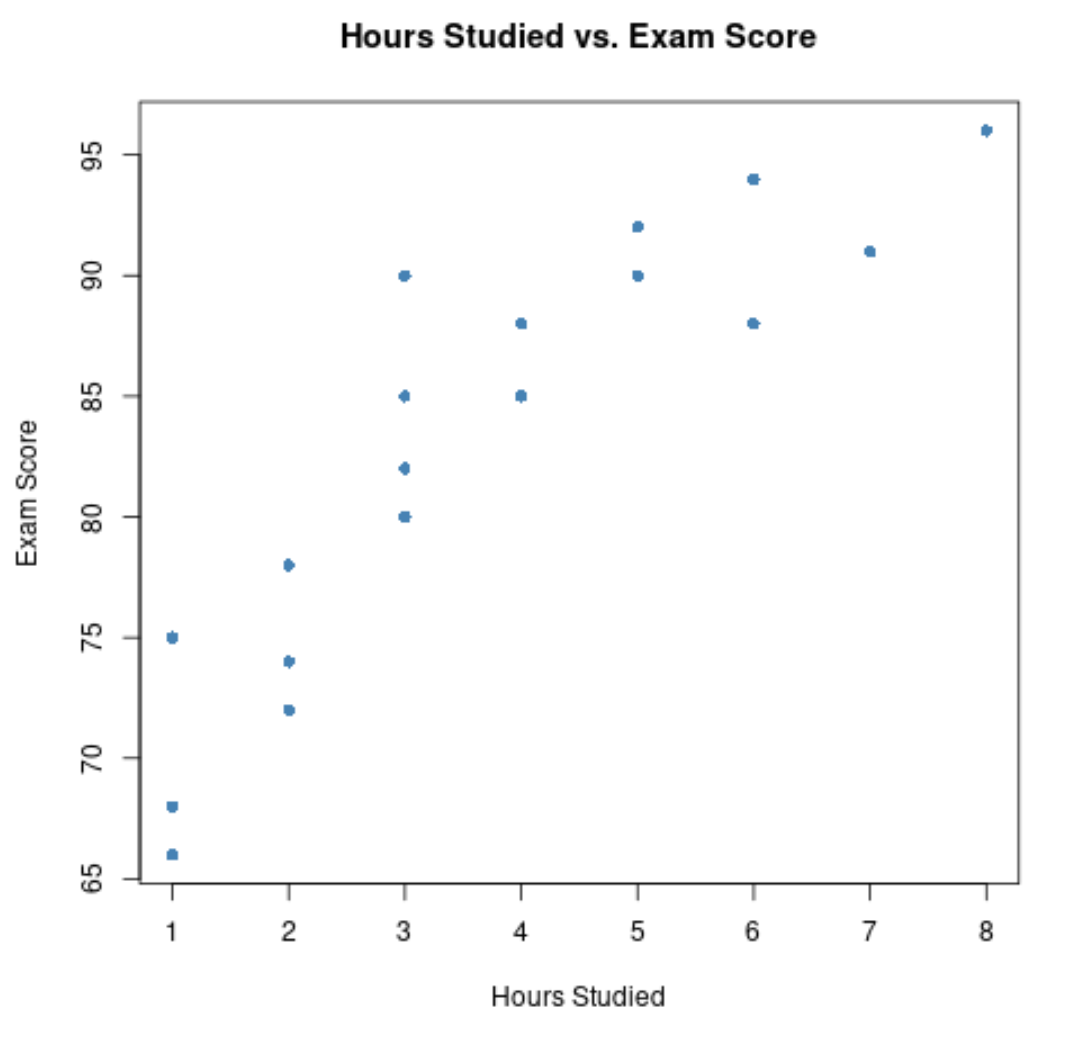
L’axe des x montre les heures étudiées et l’axe des y montre la note obtenue à l’examen.
Le graphique montre qu’il existe une relation positive entre les deux variables : à mesure que le nombre d’heures d’études augmente, les résultats aux examens ont également tendance à augmenter.
2. Coefficients de corrélation
Un coefficient de corrélation de Pearson est un moyen de quantifier la relation linéaire entre deux variables.
Nous pouvons utiliser la fonction cor() dans R pour calculer le coefficient de corrélation de Pearson entre deux variables :
#calculate correlation between hours studied and exam score received
cor(df$hours, df$score)
[1] 0.891306
Le coefficient de corrélation s’avère être de 0,891 .
Cette valeur est proche de 1, ce qui indique une forte corrélation positive entre les heures étudiées et la note obtenue à l’examen.
3. Régression linéaire simple
La régression linéaire simple est une méthode statistique que nous pouvons utiliser pour trouver l’équation de la droite qui « correspond » le mieux à un ensemble de données, que nous pouvons ensuite utiliser pour comprendre la relation exacte entre deux variables.
Nous pouvons utiliser la fonction lm() dans R pour ajuster un modèle de régression linéaire simple pour les heures étudiées et les résultats d’examen reçus :
#fit simple linear regression model fit <- lm(score ~ hours, data=df) #view summary of model summary(fit) Call: lm(formula = score ~ hours, data = df) Residuals: Min 1Q Median 3Q Max -6.920 -3.927 1.309 1.903 9.385 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 69.0734 1.9651 35.15 < 2e-16 *** hours 3.8471 0.4613 8.34 1.35e-07 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 4.171 on 18 degrees of freedom Multiple R-squared: 0.7944, Adjusted R-squared: 0.783 F-statistic: 69.56 on 1 and 18 DF, p-value: 1.347e-07
L’équation de régression ajustée s’avère être :
Score d’examen = 69,0734 + 3,8471*(heures étudiées)
Cela nous indique que chaque heure supplémentaire étudiée est associée à une augmentation moyenne de 3,8471 de la note à l’examen.
Nous pouvons également utiliser l’équation de régression ajustée pour prédire le score qu’un étudiant recevra en fonction du nombre total d’heures étudiées.
Par exemple, un étudiant qui étudie pendant 3 heures devrait obtenir un score de 81,6147 :
- Score d’examen = 69,0734 + 3,8471*(heures étudiées)
- Score d’examen = 69,0734 + 3,8471*(3)
- Résultat de l’examen = 81,6147
Ressources additionnelles
Les didacticiels suivants fournissent des informations supplémentaires sur l’analyse bivariée :
Une introduction à l’analyse bivariée
5 exemples de données bivariées dans la vie réelle
Une introduction à la régression linéaire simple
