ANOVA unidirectionnelle : définition, formule et exemple
Une ANOVA unidirectionnelle (« analyse de variance ») compare les moyennes de trois groupes indépendants ou plus pour déterminer s’il existe une différence statistiquement significative entre les moyennes de la population correspondante.
Ce tutoriel explique les éléments suivants :
- La motivation pour effectuer une ANOVA unidirectionnelle.
- Les hypothèses qui doivent être respectées pour effectuer une ANOVA unidirectionnelle.
- Le processus pour effectuer une ANOVA unidirectionnelle.
- Un exemple de la façon d’effectuer une ANOVA unidirectionnelle.
ANOVA à un facteur : motivation
Supposons que nous voulions savoir si trois programmes différents de préparation aux examens conduisent ou non à des notes moyennes différentes à un examen d’entrée à l’université. Puisqu’il y a des millions d’élèves du secondaire à travers le pays, il serait trop long et coûteux de faire le tour de chaque élève et de le laisser utiliser l’un des programmes de préparation aux examens.
Au lieu de cela, nous pourrions sélectionner trois échantillons aléatoires de 100 étudiants dans la population et permettre à chaque échantillon d’utiliser l’un des trois programmes de préparation aux tests pour se préparer à l’examen. Ensuite, nous pourrions enregistrer les scores de chaque étudiant une fois qu’il passe l’examen.
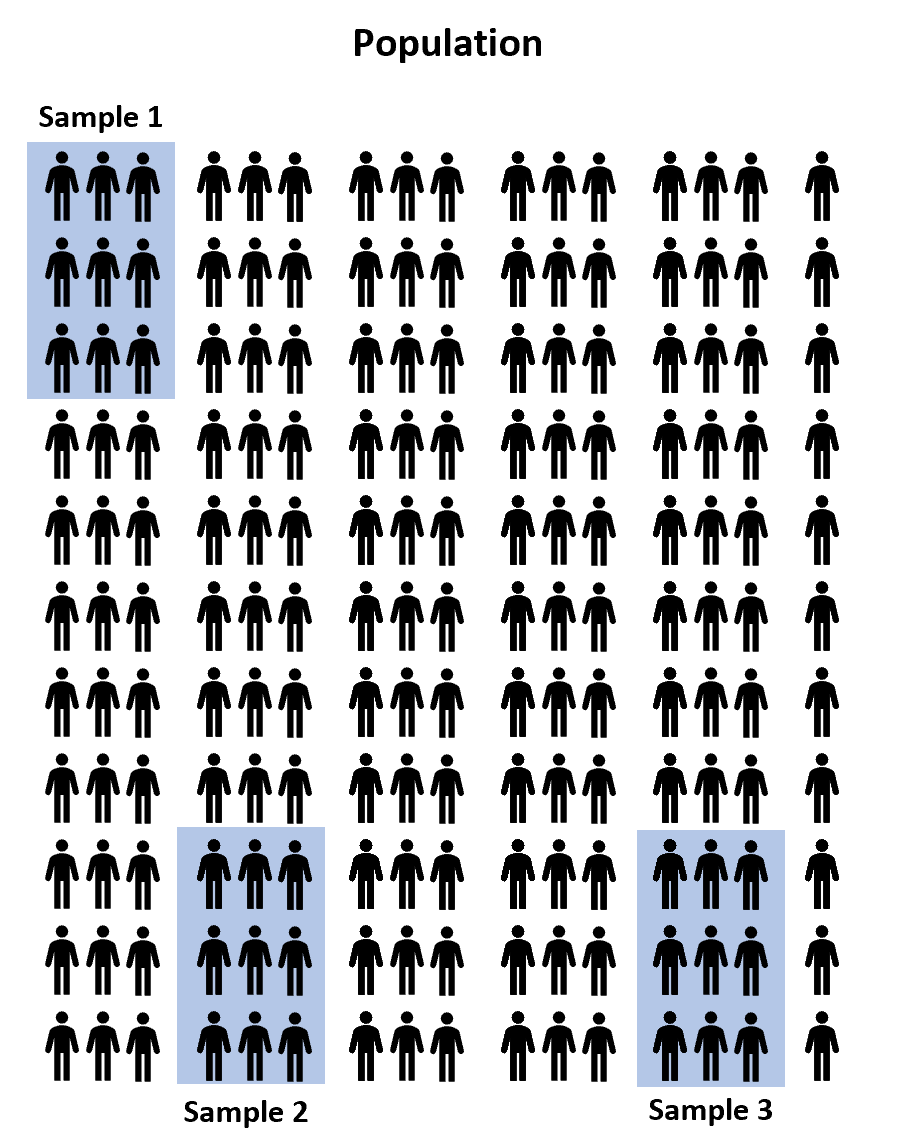
Cependant, il est pratiquement garanti que la note moyenne à l’examen entre les trois échantillons sera au moins un peu différente. La question est de savoir si cette différence est statistiquement significative . Heureusement, une ANOVA à un facteur nous permet de répondre à cette question.
ANOVA unidirectionnelle : hypothèses
Pour que les résultats d’une ANOVA unidirectionnelle soient valides, les hypothèses suivantes doivent être respectées :
1. Normalité – Chaque échantillon a été tiré d’une population normalement distribuée.
2. Variances égales – Les variances des populations dont proviennent les échantillons sont égales. Vous pouvez utiliser le test de Bartlett pour vérifier cette hypothèse.
3. Indépendance – Les observations dans chaque groupe sont indépendantes les unes des autres et les observations au sein des groupes ont été obtenues par un échantillon aléatoire.
Lisez cet article pour plus de détails sur la façon de vérifier ces hypothèses.
ANOVA unidirectionnelle : le processus
Une ANOVA unidirectionnelle utilise les hypothèses nulles et alternatives suivantes :
- H 0 (hypothèse nulle) : μ 1 = μ 2 = μ 3 = … = μ k (toutes les moyennes de population sont égales)
- H 1 (hypothèse alternative) : au moins une moyenne de population est différente du reste
Vous utiliserez généralement certains logiciels statistiques (tels que R, Excel, Stata, SPSS, etc.) pour effectuer une ANOVA unidirectionnelle, car elle est fastidieuse à réaliser manuellement.
Quel que soit le logiciel que vous utilisez, vous recevrez le tableau suivant en sortie :
| Source | Somme des carrés (SS) | df | Carrés moyens (MS) | F | p |
|---|---|---|---|---|---|
| Traitement | RSS | df r | MSR | MSR/MSE | F df r , df e |
| Erreur | ESS | df e | MSE | ||
| Total | SST | df t |
où:
- SSR : somme des carrés de régression
- SSE : somme des carrés d’erreur
- SST : somme totale des carrés (SST = SSR + SSE)
- df r : degrés de liberté de régression (df r = k-1)
- df e : degrés de liberté d’erreur (df e = nk)
- df t : degrés de liberté totaux (df t = n-1)
- k : nombre total de groupes
- n : observations totales
- MSR : carré moyen de régression (MSR = SSR/df r )
- MSE : carré moyen de l’erreur (MSE = SSE/df e )
- F : La statistique du test F (F = MSR/MSE)
- p : La valeur p qui correspond à F dfr, dfe
Si la valeur p est inférieure au niveau de signification choisi (par exemple 0,05), vous pouvez alors rejeter l’hypothèse nulle et conclure qu’au moins une des moyennes de la population est différente des autres.
Remarque : Si vous rejetez l’hypothèse nulle, cela indique qu’au moins une des moyennes de population est différente des autres, mais le tableau ANOVA ne précise pas quelles moyennes de population sont différentes. Pour le déterminer, vous devez effectuer des tests post hoc , également appelés tests de « comparaisons multiples ».
ANOVA unidirectionnelle : exemple
Supposons que nous voulions savoir si trois programmes de préparation aux examens différents conduisent ou non à des notes moyennes différentes à un examen donné. Pour tester cela, nous recrutons 30 étudiants pour participer à une étude et les répartissons en trois groupes.
Les étudiants de chaque groupe sont assignés au hasard à utiliser l’un des trois programmes de préparation aux examens pendant les trois semaines suivantes pour se préparer à un examen. A la fin des trois semaines, tous les étudiants passent le même examen.
Les résultats des examens pour chaque groupe sont indiqués ci-dessous :

Pour effectuer une ANOVA unidirectionnelle sur ces données, nous utiliserons le calculateur d’ANOVA unidirectionnel de statistique avec l’entrée suivante :

À partir du tableau de sortie, nous voyons que la statistique du test F est de 2,358 et la valeur p correspondante est de 0,11385 .

Puisque cette valeur p n’est pas inférieure à 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle.
Cela signifie que nous ne disposons pas de preuves suffisantes pour affirmer qu’il existe une différence statistiquement significative entre les résultats moyens aux examens des trois groupes.
Ressources additionnelles
Les articles suivants expliquent comment réaliser une ANOVA unidirectionnelle à l’aide de différents logiciels statistiques :
Comment effectuer une ANOVA unidirectionnelle dans Excel
Comment effectuer une ANOVA unidirectionnelle dans R
Comment effectuer une ANOVA unidirectionnelle en Python
Comment effectuer une ANOVA unidirectionnelle dans SAS
Comment effectuer une ANOVA unidirectionnelle dans SPSS
Comment effectuer une ANOVA unidirectionnelle dans Stata
Comment effectuer une ANOVA unidirectionnelle sur une calculatrice TI-84
Calculateur d’ANOVA unidirectionnel en ligne
