Comment effectuer manuellement une ANOVA bidirectionnelle

Une ANOVA bidirectionnelle est utilisée pour déterminer s’il existe ou non une différence statistiquement significative entre les moyennes de trois groupes indépendants ou plus qui ont été répartis sur deux facteurs.

Ce tutoriel explique comment réaliser manuellement une ANOVA bidirectionnelle.

Exemple : ANOVA bidirectionnelle manuelle

Supposons qu’un botaniste veuille savoir si la croissance des plantes est influencée par l’exposition au soleil et la fréquence des arrosages. Elle plante 40 graines et les laisse pousser pendant un mois dans différentes conditions d’exposition au soleil et de fréquence d’arrosage.

Au bout d’un mois, elle enregistre la hauteur de chaque plante. Les résultats sont montrés plus bas:

Dans le tableau ci-dessus, nous voyons que cinq plantes ont été cultivées dans chaque combinaison de conditions.

Par exemple, cinq plantes ont été cultivées avec un arrosage quotidien et sans lumière du soleil et leurs hauteurs après deux mois étaient de 4,8 pouces, 4,4 pouces, 3,2 pouces, 3,9 pouces et 4,4 pouces :

Nous pouvons utiliser les étapes suivantes pour effectuer une ANOVA bidirectionnelle :

Étape 1 : Calculer la somme des carrés pour le premier facteur (fréquence d’arrosage)

Tout d’abord, nous calculerons la hauteur moyenne générale des 40 plantes :

Moyenne générale = (4,8 + 5 + 6,4 + 6,3 + … + 3,9 + 4,8 + 5,5 + 5,5) / 40 = 5,1525

Ensuite, nous calculerons la hauteur moyenne de toutes les plantes arrosées quotidiennement :

Moyenne du quotidien = (4,8 + 5 + 6,4 + 6,3 + … + 4,4 + 4,8 + 5,8 + 5,8) /20 = 5,155

Ensuite, nous calculerons la hauteur moyenne de toutes les plantes arrosées chaque semaine :

Moyenne hebdomadaire = (4,4 + 4,9 + 5,8 + 6 + … + 3,9 + 4,8 + 5,5 + 5,5) /20 = 5,15

Ensuite, nous calculerons la somme des carrés pour le facteur « fréquence d’arrosage » en utilisant la formule suivante :

Σn(X _j – X ..) ²

où:

• n : la taille de l’échantillon du groupe j
• Σ : un symbole grec qui signifie « somme »
• X _j : la moyenne du groupe j
• X .. : la grande moyenne

Dans notre exemple, nous calculons la somme des carrés pour le facteur « fréquence d’arrosage » comme suit : 20(5,155-5,1525) ² + 20(5,15-5,1525) ² = 0,00025

Étape 2 : Calculer la somme des carrés pour le deuxième facteur (exposition au soleil)

Tout d’abord, nous calculerons la hauteur moyenne générale des 40 plantes :

Moyenne générale = (4,8 + 5 + 6,4 + 6,3 + … + 3,9 + 4,8 + 5,5 + 5,5) / 40 = 5,1525

Ensuite, nous calculerons la hauteur moyenne de toutes les plantes non exposées au soleil :

Moyenne sans soleil = (4,8 + 4,4 + 3,2 + 3,9 + 4,4 + 4,4 + 4,2 + 3,8 + 3,7 + 3,9) / 10 = 4,07

Nous répéterons ce calcul pour trouver la hauteur moyenne des plantes soumises à diverses expositions solaires :

• Moyenne de faible ensoleillement = 5,1
• Moyenne de lumière solaire moyenne = 5,89
• Moyenne d’ensoleillement élevé = 5,55

Ensuite, nous calculerons la somme des carrés pour le facteur « exposition au soleil » en utilisant la formule suivante :

Σn(X _j – X ..) ²

où:

• n : la taille de l’échantillon du groupe j
• Σ : un symbole grec qui signifie « somme »
• X _j : la moyenne du groupe j
• X .. : la grande moyenne

Dans notre exemple, nous calculons la somme des carrés pour le facteur « exposition au soleil » comme suit : 10(4,07-5,1525) ² + 10(5,1-5,1525) ² + 10(5,89-5,1525) ² + 10(5,55-5,1525) ² = 18,76475

Étape 3 : Calculer la somme des carrés à l’intérieur (erreur)

Ensuite, nous calculerons la somme des carrés en prenant la somme des carrés des différences entre chaque combinaison de facteurs et les hauteurs individuelles des plantes.

Par exemple, la hauteur moyenne de toutes les plantes arrosées quotidiennement sans exposition au soleil est de 4,14. Nous pouvons alors calculer la somme des carrés des différences pour chacune de ces plantes individuelles comme suit :

• SS pour arrosage quotidien et sans soleil : (4,8-4,14) ² + (4,4-4,14) ² + (3,2-4,14) ² + (3,9-4,14) ² + (4,4-4,14) ² = 1,512

Nous pouvons répéter ce processus pour chaque combinaison de facteurs :

• SS pour arrosage quotidien et faible ensoleillement : 0,928
• SS pour arrosage quotidien et ensoleillement moyen : 1,788
• SS pour arrosage quotidien et fort ensoleillement : 1,648
• SS pour un arrosage hebdomadaire et sans soleil : 0,34
• SS pour arrosage hebdomadaire et faible ensoleillement : 0,548
• SS pour arrosage hebdomadaire et ensoleillement moyen : 0,652
• SS pour arrosage hebdomadaire et fort ensoleillement : 1,268

On peut alors prendre la somme de toutes ces valeurs pour trouver la somme des carrés à l’intérieur (erreur) :

Sommes des carrés à l’intérieur = 1,512 + 0,928 + 1,788 + 1,648 + 0,34 + 0,548 + 0,652 + 1,268 = 8,684

Étape 4 : Calculer la somme totale des carrés

Ensuite, nous pouvons calculer la somme totale des carrés en prenant la somme des différences entre la hauteur de chaque plante et la moyenne générale :

Somme totale des carrés = (4,8 – 5,1525) ² + (5 – 5,1525) ² + … + (5,5 – 5,1525) ² = 28,45975

Étape 5 : Calculer l’interaction de la somme des carrés

Ensuite, nous calculerons l’interaction somme des carrés en utilisant la formule suivante :

• Interaction SS = SS Total – SS Facteur 1 – SS Facteur 2 – SS Intérieur
• Interaction SS = 28,45975 – 0,00025 – 18,76475 – 8,684
• Interaction SS = 1,01075

Étape 6 : Remplissez le tableau ANOVA

Enfin, nous remplirons les valeurs du tableau ANOVA bidirectionnel :

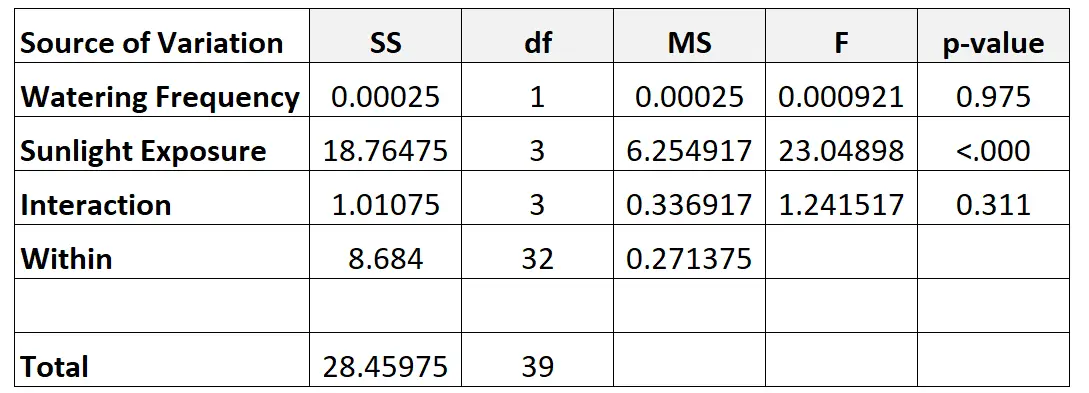
Voici comment nous avons calculé les différents nombres du tableau :

• df Fréquence d’arrosage : j-1 = 2-1 = 1
• df Exposition au soleil : k-1 = 4-1 = 3
• dfInteraction : (j-1)*(k-1) = 1*3 = 3
• df Dans : n – (j*k) = 40 – (2*4) = 32
• df total : n-1 = 40-1 = 39
• MS : SS/df
• Fréquence d’arrosage F : fréquence d’arrosage MS/MS intérieur
• F Exposition à la lumière du soleil : Exposition à la lumière du soleil MS / MS à l’intérieur
• Interaction F : Interaction MS / MS Within
• Fréquence d’arrosage de la valeur p : La valeur p qui correspond à la valeur F de 0,000921 avec le numérateur df = 1 et le dénominateur df = 32
• Valeur p d’exposition au soleil : la valeur p qui correspond à la valeur F de 23,04898 avec le numérateur df = 3 et le dénominateur df = 32
• Interaction de valeur p : La valeur p qui correspond à la valeur F de 1,241517 avec le numérateur df = 3 et le dénominateur df = 32

Remarque n°1 : n = nombre total d’observations, j = nombre de niveaux pour la fréquence d’arrosage, k = nombre de niveaux pour l’exposition au soleil.

Remarque n°2 : Les valeurs p qui correspondent à la valeur F ont été calculées à l’aide du calculateur de distribution F.

Étape 7 : Interpréter les résultats

Nous pouvons observer ce qui suit à partir du tableau ANOVA :

• La valeur p pour l’interaction entre la fréquence d’arrosage et l’exposition au soleil était de 0,311 . Ceci n’est pas statistiquement significatif à α = 0,05.
• La valeur p pour la fréquence d’arrosage était de 0,975 . Ceci n’est pas statistiquement significatif à α = 0,05.
• La valeur p pour l’exposition au soleil était <0,000 . Ceci est statistiquement significatif à α = 0,05.

Ces résultats indiquent que l’exposition au soleil est le seul facteur ayant un effet statistiquement significatif sur la hauteur des plantes.

Et comme il n’y a pas d’effet d’interaction, l’effet de l’exposition au soleil est cohérent à chaque niveau de fréquence d’arrosage.

Autrement dit, le fait qu’une plante soit arrosée quotidiennement ou hebdomadairement n’a aucun impact sur la façon dont l’exposition au soleil affecte une plante.

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur les ANOVA :

Comment effectuer manuellement une ANOVA unidirectionnelle
Comment effectuer manuellement une ANOVA à mesures répétées
Le guide complet : Comment rapporter les résultats de l’ANOVA bidirectionnelle