Distribution de Bernoulli et distribution binomiale : quelle est la différence ?

Une variable aléatoire suit une distribution de Bernoulli si elle n’a que deux résultats possibles : 0 ou 1.

Par exemple, supposons que nous lancions une pièce de monnaie une fois. Soit p . Cela signifie que la probabilité qu’il atterrisse sur pile est de 1- p .

Ainsi, nous pourrions écrire :

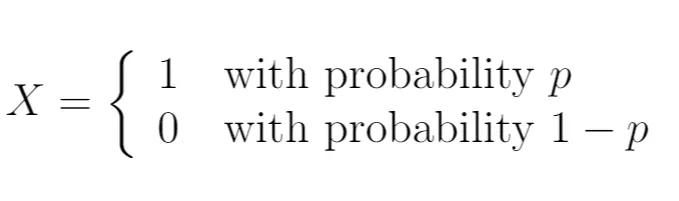
Dans ce cas, la variable aléatoire X suit une distribution de Bernoulli. Il ne peut prendre que deux valeurs possibles.

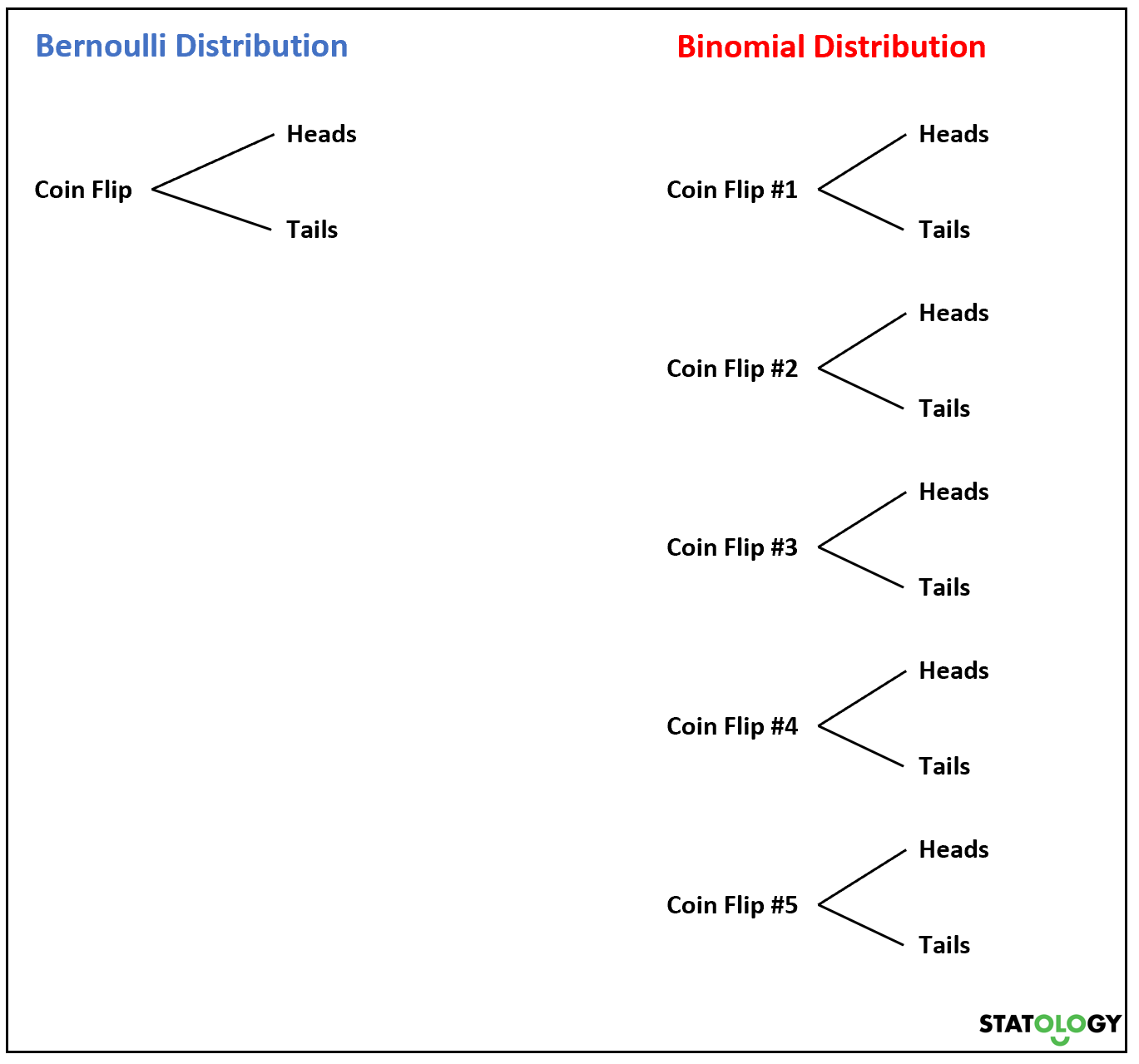
Maintenant, si nous tirons une pièce de monnaie plusieurs fois, la somme des variables aléatoires de Bernoulli suivra une distribution binomiale.

Par exemple, supposons que nous lançons une pièce de monnaie 5 fois et que nous souhaitons connaître la probabilité d’obtenir face k fois. On dirait que la variable aléatoire X suit une distribution binomiale.

Si une variable aléatoire X suit une distribution binomiale, alors la probabilité que X = k succès peut être trouvée par la formule suivante :

P(X=k) = _n C _k * p ^k * (1-p) ^nk

où:

• n : nombre d’essais
• k : nombre de réussites
• p : probabilité de succès sur un essai donné
• _n C _k : le nombre de façons d’obtenir k succès dans n essais

Par exemple, supposons que nous lançons une pièce 3 fois. On peut utiliser la formule ci-dessus pour déterminer la probabilité d’obtenir 0 face lors de ces 3 flips :

P(X=0) = ₃ C ₀ * 0,5 ⁰ * (1-0,5) ^3-0 = 1 * 1 * (0,5) ³ = 0,125

Lorsque n = 1 essai, la distribution binomiale est équivalente à la distribution de Bernoulli.

Notes IMPORTANTES

Voici quelques remarques importantes concernant la distribution de Bernoulli et Binomial :

1. Une variable aléatoire qui suit une distribution de Bernoulli ne peut prendre que deux valeurs possibles, mais une variable aléatoire qui suit une distribution binomiale peut prendre plusieurs valeurs.

Par exemple, lors d’un seul tirage au sort, nous aurons soit 0, soit 1 face. Cependant, dans une série de 5 tirages au sort, nous pourrions avoir 0, 1, 2, 3, 4 ou 5 faces.

2. Pour qu’une variable aléatoire suive une distribution binomiale, la probabilité de « succès » dans chaque essai de Bernoulli doit être égale et indépendante.

Par exemple, si nous définissons le « succès » comme atterrir sur face, alors la probabilité de succès à chaque tirage au sort est égale à 0,5 et chaque lancer est indépendant – le résultat d’un tirage au sort n’affecte pas le résultat d’un autre.

Ressources additionnelles

Une introduction aux expériences binomiales
Une introduction à la distribution binomiale
Comprendre la forme d’une distribution binomiale